名校
1 . 甲、乙两人进行象棋比赛,赛前每人有3面小红旗.一局比赛后输者需给赢者一面小红旗;若是平局就不需要给红旗,当其中一方无小红旗时,比赛结束,有6面小红旗者最终获胜.根据以往两人的比赛结果可知,在一局比赛中甲胜的概率为 ,乙胜的概率为
,乙胜的概率为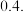
(1)设第一局比赛后甲的红旗个数为 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)求比赛共进行五局且甲获胜的概率;
(3)若比赛一共进行五局且第一局是乙胜,求此条件下甲最终获胜的概率(结果保留两位有效数字).
 ,乙胜的概率为
,乙胜的概率为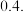
(1)设第一局比赛后甲的红旗个数为
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)求比赛共进行五局且甲获胜的概率;
(3)若比赛一共进行五局且第一局是乙胜,求此条件下甲最终获胜的概率(结果保留两位有效数字).
您最近一年使用:0次
7日内更新
|
271次组卷
|
2卷引用:四川省内江市威远中学校2024-2025学年高三上学期期中考试数学试题
名校
解题方法
2 . 全国执业医师证考试分实践技能考试与医学综合笔试两部分,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则执业医师考试“合格”,并颁发执业医师证书.甲、乙、丙三人在医学综合笔试中“合格”的概率依次为 ,
, ,
, ,在实践技能考试中“合格”的概率依次为
,在实践技能考试中“合格”的概率依次为 ,
, ,
, ,所有考试是否合格互不影响.
,所有考试是否合格互不影响.
(1)求甲没有获得执业医师证书的概率;
(2)这三人进行实践技能考试与医学综合理论考试两项考试后,求恰有两人获得执业医师证书的概率.
 ,
, ,
, ,在实践技能考试中“合格”的概率依次为
,在实践技能考试中“合格”的概率依次为 ,
, ,
, ,所有考试是否合格互不影响.
,所有考试是否合格互不影响.(1)求甲没有获得执业医师证书的概率;
(2)这三人进行实践技能考试与医学综合理论考试两项考试后,求恰有两人获得执业医师证书的概率.
您最近一年使用:0次
2024-10-15更新
|
952次组卷
|
3卷引用:四川省南充高级中学2024-2025学年高三上学期10月检测数学试题
解题方法
3 . 甲、乙两名同学进行定点投篮训练,据以往训练数据,甲每次投篮命中的概率为 ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为 ,各次投篮互不影响、现甲、乙两人开展多轮次的定点投篮活动,每轮次各投
,各次投篮互不影响、现甲、乙两人开展多轮次的定点投篮活动,每轮次各投 个球,每投进一个球记
个球,每投进一个球记 分,未投进记
分,未投进记 分.
分.
(1)求甲在一轮投篮结束后的得分不大于 的概率;
的概率;
(2)记甲、乙每轮投篮得分之和为 .
.
①求 的分布列和数学期望;
的分布列和数学期望;
②若 ,则称该轮次为一个“成功轮次”.在连续
,则称该轮次为一个“成功轮次”.在连续 轮次的投篮活动中,记“成功轮次”为
轮次的投篮活动中,记“成功轮次”为 ,当
,当 为何值时,
为何值时,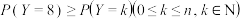 恒成立?
恒成立?
 ,乙每次投篮命中的概率为
,乙每次投篮命中的概率为 ,各次投篮互不影响、现甲、乙两人开展多轮次的定点投篮活动,每轮次各投
,各次投篮互不影响、现甲、乙两人开展多轮次的定点投篮活动,每轮次各投 个球,每投进一个球记
个球,每投进一个球记 分,未投进记
分,未投进记 分.
分.(1)求甲在一轮投篮结束后的得分不大于
 的概率;
的概率;(2)记甲、乙每轮投篮得分之和为
 .
.①求
 的分布列和数学期望;
的分布列和数学期望;②若
 ,则称该轮次为一个“成功轮次”.在连续
,则称该轮次为一个“成功轮次”.在连续 轮次的投篮活动中,记“成功轮次”为
轮次的投篮活动中,记“成功轮次”为 ,当
,当 为何值时,
为何值时,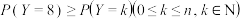 恒成立?
恒成立?
您最近一年使用:0次
名校
解题方法
4 . 良好的用眼习惯能够从多方面保护眼睛的健康,降低近视发生的可能性,对于保护青少年的视力具有不可替代的重要作用.某班班主任为了让本班学生能够掌握良好的用眼习惯,开展了“爱眼护眼”有奖知识竞赛活动,班主任将竞赛题目分为 两组,规定每名学生从
两组,规定每名学生从 两组题目中各随机抽取2道题作答.已知该班学生甲答对
两组题目中各随机抽取2道题作答.已知该班学生甲答对 组题的概率均为
组题的概率均为 ,答对
,答对 组题的概率均为
组题的概率均为 .假设学生甲每道题是否答对相互独立.
.假设学生甲每道题是否答对相互独立.
(1)求学生甲恰好答对3道题的概率;
(2)设学生甲共答对了 道题,求
道题,求 的分布列及数学期望.
的分布列及数学期望.
 两组,规定每名学生从
两组,规定每名学生从 两组题目中各随机抽取2道题作答.已知该班学生甲答对
两组题目中各随机抽取2道题作答.已知该班学生甲答对 组题的概率均为
组题的概率均为 ,答对
,答对 组题的概率均为
组题的概率均为 .假设学生甲每道题是否答对相互独立.
.假设学生甲每道题是否答对相互独立.(1)求学生甲恰好答对3道题的概率;
(2)设学生甲共答对了
 道题,求
道题,求 的分布列及数学期望.
的分布列及数学期望.
您最近一年使用:0次
2024-09-19更新
|
876次组卷
|
4卷引用:四川省眉山市彭山区第一中学2025届高三上学期开学考试数学试题(非补习班)
四川省眉山市彭山区第一中学2025届高三上学期开学考试数学试题(非补习班)内蒙古赤峰红旗中学2024-2025学年高三上学期第一次月考数学试题(已下线)第三章 随机变量及其分布列 专题一 随机变量的期望 微点2 随机变量的分布列、期望综合训练【基础版】陕西省西安建筑科技大学附属中学2025届高三上学期第一次模拟考试数学试卷
名校
解题方法
5 . 甲、乙两名运动员进行乒乓球比赛,规定每局比赛胜者得1分,负者得0分,比赛一直进行到一方比另一方多两分为止,多得两分的一方赢得比赛.已知每局比赛中,甲获胜的概率为 ,乙获胜的概率为
,乙获胜的概率为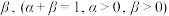 ,且每局比赛结果相互独立.若比赛最多进行5局,则比赛结束时比赛局数
,且每局比赛结果相互独立.若比赛最多进行5局,则比赛结束时比赛局数 的期望
的期望 的最大值为
的最大值为__________ .
 ,乙获胜的概率为
,乙获胜的概率为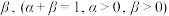 ,且每局比赛结果相互独立.若比赛最多进行5局,则比赛结束时比赛局数
,且每局比赛结果相互独立.若比赛最多进行5局,则比赛结束时比赛局数 的期望
的期望 的最大值为
的最大值为
您最近一年使用:0次
名校
解题方法
6 . 夏日天气炎热,学校为高三备考的同学准备了绿豆汤和银耳羹两种凉饮,某同学每天都会在两种凉饮中选择一种,已知该同学第1天选择绿豆汤的概率是 ,若在前一天选择绿豆汤的条件下,后一天继续选择绿豆汤的概率为
,若在前一天选择绿豆汤的条件下,后一天继续选择绿豆汤的概率为 ,而在前一天选择银耳羹的条件下,后一天继续选择银耳羹的概率为
,而在前一天选择银耳羹的条件下,后一天继续选择银耳羹的概率为 ,如此往复.(提示:设
,如此往复.(提示:设 表示第
表示第 天选择绿豆汤)
天选择绿豆汤)
(1)求该同学第一天和第二天都选择绿豆汤的概率
(2)求该同学第2天选择绿豆汤的概率;
(3)记该同学第 天选择绿豆汤的概率为
天选择绿豆汤的概率为 ,求出
,求出 的通项公式.
的通项公式.
 ,若在前一天选择绿豆汤的条件下,后一天继续选择绿豆汤的概率为
,若在前一天选择绿豆汤的条件下,后一天继续选择绿豆汤的概率为 ,而在前一天选择银耳羹的条件下,后一天继续选择银耳羹的概率为
,而在前一天选择银耳羹的条件下,后一天继续选择银耳羹的概率为 ,如此往复.(提示:设
,如此往复.(提示:设 表示第
表示第 天选择绿豆汤)
天选择绿豆汤)(1)求该同学第一天和第二天都选择绿豆汤的概率
(2)求该同学第2天选择绿豆汤的概率;
(3)记该同学第
 天选择绿豆汤的概率为
天选择绿豆汤的概率为 ,求出
,求出 的通项公式.
的通项公式.
您最近一年使用:0次
2024-09-12更新
|
637次组卷
|
4卷引用:四川省内江市威远县威远中学校2024-2025学年高三上学期9月月考数学试题
名校
7 . 在某象棋比赛中,若选手甲和选手乙进入了最终的象棋决赛,经赛前数据统计发现在每局象棋比赛中甲和乙获胜的概率分别为 和
和 ,且决赛赛制为
,且决赛赛制为 局
局 胜制,求:
胜制,求:
(1)前 局中乙恰有
局中乙恰有 局获胜的概率;
局获胜的概率;
(2)比赛结束时两位选手共进行了 局比赛的概率.
局比赛的概率.
 和
和 ,且决赛赛制为
,且决赛赛制为 局
局 胜制,求:
胜制,求:(1)前
 局中乙恰有
局中乙恰有 局获胜的概率;
局获胜的概率;(2)比赛结束时两位选手共进行了
 局比赛的概率.
局比赛的概率.
您最近一年使用:0次
2024-09-10更新
|
554次组卷
|
2卷引用:四川省绵阳中学2025届高三上学期9月份联考数学试题
名校
解题方法
8 . 甲、乙、丙、丁、戊、己 名同学相互做传接球训练,球从甲手中开始,等可能地随机传向另外
名同学相互做传接球训练,球从甲手中开始,等可能地随机传向另外 人中的
人中的 人,接球者接到球后再等可能地随机传向另外
人,接球者接到球后再等可能地随机传向另外 人中的
人中的 人,如此不停地传下去,假设传出的球都能被接住.记第
人,如此不停地传下去,假设传出的球都能被接住.记第 次传球之后球在乙手中的概率为
次传球之后球在乙手中的概率为 ,则
,则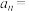
______ .
 名同学相互做传接球训练,球从甲手中开始,等可能地随机传向另外
名同学相互做传接球训练,球从甲手中开始,等可能地随机传向另外 人中的
人中的 人,接球者接到球后再等可能地随机传向另外
人,接球者接到球后再等可能地随机传向另外 人中的
人中的 人,如此不停地传下去,假设传出的球都能被接住.记第
人,如此不停地传下去,假设传出的球都能被接住.记第 次传球之后球在乙手中的概率为
次传球之后球在乙手中的概率为 ,则
,则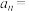
您最近一年使用:0次
名校
解题方法
9 . 算盘是我国古代一项伟大的发明,是一类重要的计算工具.如图,算盘多为木制,内嵌有九至十五根直杆(简称档),自右向左分别表示个位、十位、百位、……,梁上面一粒珠子(简称上珠)代表5,梁下面一粒珠子(简称下珠)代表1,五粒下珠的大小等于同组一粒上珠的大小.例如,个位拨动一粒上珠、十位拨动一粒下珠至梁上,表示数字15.现将算盘的个位、十位、百位分别随机拨动一粒珠子至梁上,设事件 “表示的三位数能被5整除”,
“表示的三位数能被5整除”, “表示的三位数能被3整除”.
“表示的三位数能被3整除”.
(2)求事件 、
、 的概率.
的概率.
 “表示的三位数能被5整除”,
“表示的三位数能被5整除”, “表示的三位数能被3整除”.
“表示的三位数能被3整除”.
(2)求事件
 、
、 的概率.
的概率.
您最近一年使用:0次
2024-09-08更新
|
323次组卷
|
3卷引用:四川省新高考联盟校级2025届高三九月适应考数学试题
四川省新高考联盟校级2025届高三九月适应考数学试题(已下线)第五章 概率统计创新问题 专题六 概率统计中的数学文化 微点1 概率统计与数学文化的交汇(一)【培优版】宁夏回族自治区西吉中学2023-2024年高一下学期期末考试数学试题
解题方法
10 . 条件概率与条件期望是现代概率体系中的重要概念,近年来,条件概率和条件期望已被广泛的应用到日常生产生活中.定义:设 ,
, 是离散型随机变量,则
是离散型随机变量,则 在给定事件
在给定事件 条件下的期望为
条件下的期望为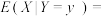
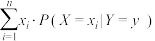
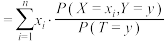 ,其中
,其中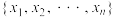 为
为 的所有可能取值集合,
的所有可能取值集合,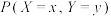 表示事件“
表示事件“ ”与事件“
”与事件“ ”都发生的概率.某商场进行促销活动,凡在该商场每消费500元,可有2次抽奖机会,每次获奖的概率均为
”都发生的概率.某商场进行促销活动,凡在该商场每消费500元,可有2次抽奖机会,每次获奖的概率均为 ,某人在该商场消费了1000元,共获得4次抽奖机会.设
,某人在该商场消费了1000元,共获得4次抽奖机会.设 表示第一次抽中奖品时的抽取次数,
表示第一次抽中奖品时的抽取次数, 表示第二次抽中奖品时的抽取次数.则
表示第二次抽中奖品时的抽取次数.则
________ .
 ,
, 是离散型随机变量,则
是离散型随机变量,则 在给定事件
在给定事件 条件下的期望为
条件下的期望为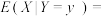
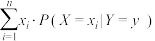
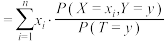 ,其中
,其中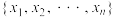 为
为 的所有可能取值集合,
的所有可能取值集合,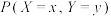 表示事件“
表示事件“ ”与事件“
”与事件“ ”都发生的概率.某商场进行促销活动,凡在该商场每消费500元,可有2次抽奖机会,每次获奖的概率均为
”都发生的概率.某商场进行促销活动,凡在该商场每消费500元,可有2次抽奖机会,每次获奖的概率均为 ,某人在该商场消费了1000元,共获得4次抽奖机会.设
,某人在该商场消费了1000元,共获得4次抽奖机会.设 表示第一次抽中奖品时的抽取次数,
表示第一次抽中奖品时的抽取次数, 表示第二次抽中奖品时的抽取次数.则
表示第二次抽中奖品时的抽取次数.则
您最近一年使用:0次



