真题
名校
1 . 某投篮比赛分为两个阶段,每个参赛队由两名队员组成,比赛具体规则如下:第一阶段由参赛队中一名队员投篮3次,若3次都未投中,则该队被淘汰,比赛成绩为0分;若至少投中一次,则该队进入第二阶段.第二阶段由该队的另一名队员投篮3次,每次投篮投中得5分,未投中得0分.该队的比赛成绩为第二阶段的得分总和.某参赛队由甲、乙两名队员组成,设甲每次投中的概率为p,乙每次投中的概率为q,各次投中与否相互独立.
(1)若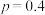 ,
,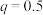 ,甲参加第一阶段比赛,求甲、乙所在队的比赛成绩不少于5分的概率.
,甲参加第一阶段比赛,求甲、乙所在队的比赛成绩不少于5分的概率.
(2)假设 ,
,
(i)为使得甲、乙所在队的比赛成绩为15分的概率最大,应该由谁参加第一阶段比赛?
(ii)为使得甲、乙所在队的比赛成绩的数学期望最大,应该由谁参加第一阶段比赛?
(1)若
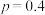 ,
,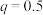 ,甲参加第一阶段比赛,求甲、乙所在队的比赛成绩不少于5分的概率.
,甲参加第一阶段比赛,求甲、乙所在队的比赛成绩不少于5分的概率.(2)假设
 ,
,(i)为使得甲、乙所在队的比赛成绩为15分的概率最大,应该由谁参加第一阶段比赛?
(ii)为使得甲、乙所在队的比赛成绩的数学期望最大,应该由谁参加第一阶段比赛?
您最近一年使用:0次
2024-06-07更新
|
20470次组卷
|
18卷引用:贵州省贵阳市南明区部分学校2023-2024学年高二下学期6月联考数学试题
(已下线)贵州省贵阳市南明区部分学校2023-2024学年高二下学期6月联考数学试题贵州省贵阳市南明区部分学校2023-2024学年高二下学期6月联考数学试题(已下线)作业03 概率(2)-【暑假分层作业】(苏教版2019选择性必修第二册)宁夏石嘴山市平罗县平罗中学2023-2024学年高二下学期期末考试数学试卷(重点班)2024年新课标全国Ⅱ卷数学真题(已下线)2024年高考数学真题完全解读(新高考Ⅱ卷)专题10计数原理、概率、随机变量及其分布(已下线)2024年新课标全国Ⅱ卷数学真题变式题16-19(已下线)五年新高考专题08计数原理与概率统计(已下线)三年新高考专题08计数原理与概率统计(已下线)专题11 概率(4大考向真题解读)(已下线)专题1 概率压轴大题(过关集训)(已下线)专题2 随机变量及其分布压轴大题(一)【讲】宁夏银川市永宁县上游高级中学2025届高三上学期开学考试数学试题(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点1 重要的概率分布模型(一)【培优版】四川省仁寿第一中学校南校区2024-2025学年高三上学期9月月考数学试题(已下线)第06讲 事件的相互独立性、条件概率与全概率公式(七大题型)(练习)(已下线)第07讲 离散型随机变量及其分布列、数字特征(六大题型)(练习)
名校
解题方法
2 . 将2n(n∈N*)个有编号的球随机放入2个不同的盒子中,已知每个球放入这2个盒子的可能性相同,且每个盒子容纳球数不限记2个盒子中最少的球数为X(0≤X≤n,X∈N*),则下列说法中正确的有( )
A.当n=1时,方差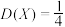 |
B.当n=2时,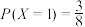 |
C.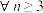 , ,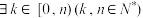 ,使得P(X=k)>P(X=k+1)成立 ,使得P(X=k)>P(X=k+1)成立 |
D.当n确定时,期望 |
您最近一年使用:0次
2021-05-28更新
|
2338次组卷
|
8卷引用:贵州省遵义清华中学2022-2023学年高二下学期第一次月考数学试题



