1 . ”鸡兔同笼”我国隋朝时期数学著作《孙子算经》中的一个有趣题目:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”
(1)求出鸡、兔各几只?
(2)根据提示,设计这类问题的通用解法,并画出算法的程序框图.
解:设有 只鸡,
只鸡, 只兔,总头数为
只兔,总头数为 ,总脚数为
,总脚数为 ,则
,则 ,解方程得:
,解方程得: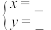
用数学语言:
第一步:输入______,______;
第二步:计算鸡的只数______;
第三步:计算兔的只数______;
第四步:输出______.
(1)求出鸡、兔各几只?
(2)根据提示,设计这类问题的通用解法,并画出算法的程序框图.
解:设有
 只鸡,
只鸡, 只兔,总头数为
只兔,总头数为 ,总脚数为
,总脚数为 ,则
,则 ,解方程得:
,解方程得: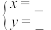
用数学语言:
第一步:输入______,______;
第二步:计算鸡的只数______;
第三步:计算兔的只数______;
第四步:输出______.

您最近一年使用:0次
2 . 下列所给问题中,不可以设计一个算法求解的是
| A.求1+2+3+…+10的和 | B.解方程组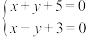 |
| C.求半径为3的圆的面积 | D.预测下一期体育彩票的中奖号码 |
您最近一年使用:0次
3 . 写出求方程组 的解的算法.
的解的算法.
 的解的算法.
的解的算法.
您最近一年使用:0次
名校
4 . 下列描述不是解决问题的算法的是
| A.从中山到北京先坐汽车,再坐火车 |
| B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、化系数为1 |
C.方程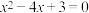 有两个不相等的实根 有两个不相等的实根 |
D.求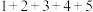 的值,先计算 的值,先计算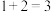 ,再由 ,再由 ,最终结果为15 ,最终结果为15 |
您最近一年使用:0次
2020-03-04更新
|
284次组卷
|
4卷引用:陕西省商洛市洛南县2018-2019学年高一下学期期中数学试题
陕西省商洛市洛南县2018-2019学年高一下学期期中数学试题(已下线)专题01 算法的概念(基础练)-2020-2021学年高一数学十分钟同步课堂专练(人教A版必修3)宁夏银川市兴庆区2022-2023学年高二上学期期中联考数学试题宁夏回族自治区银川一中2022-2023学年高二上学期期中考试数学试题
5 . 看下面的四段话,其中不是解决问题的算法的是( )
| A.从上海到北京看奥运会开幕式,先坐公交车,再坐飞机,然后乘地铁抵达 |
| B.解一元一次方程的步骤是:去分母、去括号、移项、合并同类项、系数化为1 |
C.方程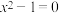 有两个实数根 有两个实数根 |
D.求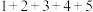 的值,先计算 的值,先计算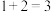 ,再计算 ,再计算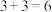 , ,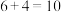 , , ,最终结果为15 ,最终结果为15 |
您最近一年使用:0次
6 . 下列语句表达中是算法的个数为 ( )
①从济南去巴黎可以先乘火车到北京,再乘飞机到巴黎;
②利用公式S= ah计算底为1,高为2的三角形的面积;
ah计算底为1,高为2的三角形的面积;
③解不等式 x>2x+4;
x>2x+4;
④求过点M(1,2)与点N(-3,-5)的直线的方程,可先求直线的斜率,再利用点斜式求得方程.
①从济南去巴黎可以先乘火车到北京,再乘飞机到巴黎;
②利用公式S=
 ah计算底为1,高为2的三角形的面积;
ah计算底为1,高为2的三角形的面积;③解不等式
 x>2x+4;
x>2x+4;④求过点M(1,2)与点N(-3,-5)的直线的方程,可先求直线的斜率,再利用点斜式求得方程.
| A.1 | B.2 | C.3 | D.4 |
您最近一年使用:0次
7 . 下列算法中含有条件结构的是( )
| A.求点到直线的距离 |
| B.已知三角形三边长求面积 |
C.解一元二次方程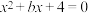  |
| D.求两个数的平方和 |
您最近一年使用:0次
8 . 下列算法中,含有条件分支结构的是
| A.求两个数的积 |
| B.求点到直线的距离 |
| C.解一元二次不等式 |
| D.已知梯形两底和高求面积 |
您最近一年使用:0次



