阅读下面求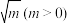 近似值的方法,回答问题:
近似值的方法,回答问题:
①任取正数 ;
;
②令 则
则 ;
;
③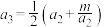 ,则
,则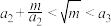 ;
;
……以此类推 次,得到
次,得到
其中 称为
称为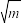 的
的 阶过剩近似值,
阶过剩近似值,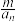 称为
称为 的
的 阶不足近似值. 仿照上述方法,求 6 的近似值.
阶不足近似值. 仿照上述方法,求 6 的近似值.
①取正数 .
.
②于是 ;则_______
;则_______
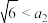
③ 的 3 阶过剩近似值
的 3 阶过剩近似值 是_______,3 阶不足近似值是________
是_______,3 阶不足近似值是________
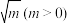 近似值的方法,回答问题:
近似值的方法,回答问题:①任取正数
 ;
;②令
 则
则 ;
;③
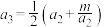 ,则
,则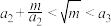 ;
;……以此类推
 次,得到
次,得到
其中
 称为
称为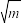 的
的 阶过剩近似值,
阶过剩近似值,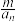 称为
称为 的
的 阶不足近似值. 仿照上述方法,求 6 的近似值.
阶不足近似值. 仿照上述方法,求 6 的近似值. ①取正数
 .
.②于是
 ;则_______
;则_______
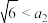
③
 的 3 阶过剩近似值
的 3 阶过剩近似值 是_______,3 阶不足近似值是________
是_______,3 阶不足近似值是________
更新时间:2020/05/15 22:16:25
|
相似题推荐
解答题-作图题
|
适中
(0.65)
【推荐1】在5×4的网格中,每个小正方形的边长是1个单位长.
(1)先在图中将面积是5的一个长方形分割成5块,然后再画出用这5块拼成的一个正方形;
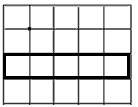
(2)设拼成的正方形的边长为a个单位长,
①a是有理数还是无理数?
②试在数轴上将a的相反数表示出来;
③求出a的近似值(保留一位小数)
(1)先在图中将面积是5的一个长方形分割成5块,然后再画出用这5块拼成的一个正方形;

(2)设拼成的正方形的边长为a个单位长,
①a是有理数还是无理数?
②试在数轴上将a的相反数表示出来;
③求出a的近似值(保留一位小数)
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
【推荐2】先阅读下面的文字,然后解答问题.
大家知道 是无理数,而无理数是无限不循环小数
是无理数,而无理数是无限不循环小数 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用 的小数部分,你同意小明的表示方法吗?事实上,因为
的小数部分,你同意小明的表示方法吗?事实上,因为 的整数部分是1,差就是小数部分.
的整数部分是1,差就是小数部分.
由此我们还可以得到一个真命题:如果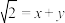 ,其中x是整数,那么
,其中x是整数,那么 ,
,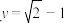
请解答下列问题:
(1)如果 ,其中
,其中 是整数, 且
是整数, 且 ,那么
,那么 ,
, ;
;
(2)已知 ,其中
,其中 是整数, 且
是整数, 且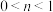 ,求
,求 的值.
的值.
大家知道
 是无理数,而无理数是无限不循环小数
是无理数,而无理数是无限不循环小数 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用 的小数部分,你同意小明的表示方法吗?事实上,因为
的小数部分,你同意小明的表示方法吗?事实上,因为 的整数部分是1,差就是小数部分.
的整数部分是1,差就是小数部分.由此我们还可以得到一个真命题:如果
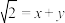 ,其中x是整数,那么
,其中x是整数,那么 ,
,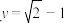
请解答下列问题:
(1)如果
 ,其中
,其中 是整数, 且
是整数, 且 ,那么
,那么 ,
, ;
;(2)已知
 ,其中
,其中 是整数, 且
是整数, 且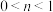 ,求
,求 的值.
的值.
您最近一年使用:0次
解答题-计算题
|
适中
(0.65)
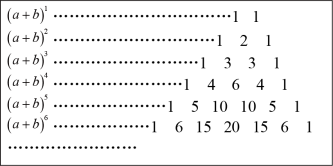
【推荐1】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.下面我们依次对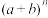 展开式的各项系数进一步研究发现,当
展开式的各项系数进一步研究发现,当 取正整数时可以单独列成表中的形式:
取正整数时可以单独列成表中的形式:
例如,在三角形中第二行的三个数1,2,1,恰好对应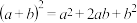 展开式中的系数,
展开式中的系数,
(1)根据表中规律,写出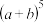 的展开式;
的展开式;
(2)多项式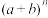 的展开式是一个几次几项式?并预测第三项的系数;
的展开式是一个几次几项式?并预测第三项的系数;
(3)请你猜想多项式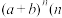 取正整数)的展开式的各项系数之和(结果用含字母
取正整数)的展开式的各项系数之和(结果用含字母 的代数式表示);
的代数式表示);
(4)利用表中规律计算: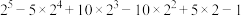 (不用表中规律计算不给分).
(不用表中规律计算不给分).
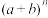 展开式的各项系数进一步研究发现,当
展开式的各项系数进一步研究发现,当 取正整数时可以单独列成表中的形式:
取正整数时可以单独列成表中的形式:例如,在三角形中第二行的三个数1,2,1,恰好对应
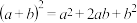 展开式中的系数,
展开式中的系数, 
(1)根据表中规律,写出
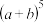 的展开式;
的展开式;(2)多项式
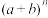 的展开式是一个几次几项式?并预测第三项的系数;
的展开式是一个几次几项式?并预测第三项的系数;(3)请你猜想多项式
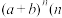 取正整数)的展开式的各项系数之和(结果用含字母
取正整数)的展开式的各项系数之和(结果用含字母 的代数式表示);
的代数式表示);(4)利用表中规律计算:
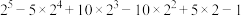 (不用表中规律计算不给分).
(不用表中规律计算不给分).
您最近一年使用:0次
【推荐2】阅读理解,解答下列问题:
在平面直角坐标系中,对于点 若点
若点 的坐标为
的坐标为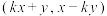 ,则称点
,则称点 为点
为点 的“
的“ 级牵挂点”,如点
级牵挂点”,如点 的“
的“ 级牵挂点”为
级牵挂点”为 ,即
,即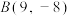 .
.
(1)已知点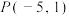 的“
的“ 级牵挂点”为
级牵挂点”为 求点
求点 的坐标,并求出点
的坐标,并求出点 到
到 轴的距离;
轴的距离;
(2)已知点 的“
的“ 级牵挂点”为
级牵挂点”为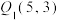 ,求
,求 点的坐标及所在象限;
点的坐标及所在象限;
(3)如果点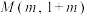 的“
的“ 级牵挂点”
级牵挂点” 在
在 轴上,求点
轴上,求点 的坐标;
的坐标;
(4)如果点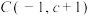 的“
的“ 级牵挂点”
级牵挂点” 在第二象限,
在第二象限,
①求 的取值范围;
的取值范围;
②在①中,当 取最大整数时,过点
取最大整数时,过点 作
作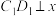 轴于点
轴于点 ,连接
,连接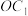 ,将
,将 平移得到
平移得到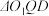 ,其中
,其中 、
、 、
、 的对应点分别为
的对应点分别为 、
、 、
、 ,连接
,连接 ,直接写出四边形
,直接写出四边形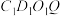 的面积为______.
的面积为______.
在平面直角坐标系中,对于点
 若点
若点 的坐标为
的坐标为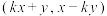 ,则称点
,则称点 为点
为点 的“
的“ 级牵挂点”,如点
级牵挂点”,如点 的“
的“ 级牵挂点”为
级牵挂点”为 ,即
,即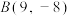 .
.
(1)已知点
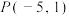 的“
的“ 级牵挂点”为
级牵挂点”为 求点
求点 的坐标,并求出点
的坐标,并求出点 到
到 轴的距离;
轴的距离;(2)已知点
 的“
的“ 级牵挂点”为
级牵挂点”为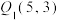 ,求
,求 点的坐标及所在象限;
点的坐标及所在象限;(3)如果点
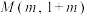 的“
的“ 级牵挂点”
级牵挂点” 在
在 轴上,求点
轴上,求点 的坐标;
的坐标;(4)如果点
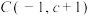 的“
的“ 级牵挂点”
级牵挂点” 在第二象限,
在第二象限,①求
 的取值范围;
的取值范围;②在①中,当
 取最大整数时,过点
取最大整数时,过点 作
作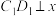 轴于点
轴于点 ,连接
,连接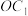 ,将
,将 平移得到
平移得到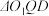 ,其中
,其中 、
、 、
、 的对应点分别为
的对应点分别为 、
、 、
、 ,连接
,连接 ,直接写出四边形
,直接写出四边形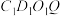 的面积为______.
的面积为______.
您最近一年使用:0次

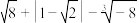 .
.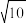 的整数部分,B是它的小数部分,求
的整数部分,B是它的小数部分,求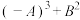 的值.
的值.
 的最大或最小值时,通过利用公式
的最大或最小值时,通过利用公式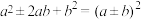 对式子作如下变形:
对式子作如下变形: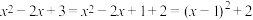 ,
,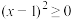 ,
,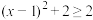 ,
,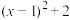 有最小值2,
有最小值2,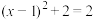 ,
, 的最大值为7.
的最大值为7.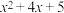 的最小值为______________;代数式
的最小值为______________;代数式 的最大值为______________;
的最大值为______________;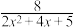 的最大或最小值,并写出对应的
的最大或最小值,并写出对应的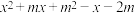 的最大或最小值,并写出对应的
的最大或最小值,并写出对应的

