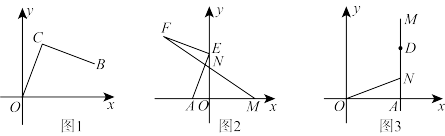
如图,Rt△ABC,∠ACB=90°,AC=BC,已知点A和点C的坐标分别为(0,2)和(﹣1,0),过点A、B的直线关系式为y=kx+b.
(1)求点B的坐标和直线AB的函数关系式;
(2)在第二象限y=kx+b的图象上是否存在点P,使△ACP的面积为4?若存在;请求出符合条件的点P的坐标;若不存在,请说明理由.
(1)求点B的坐标和直线AB的函数关系式;
(2)在第二象限y=kx+b的图象上是否存在点P,使△ACP的面积为4?若存在;请求出符合条件的点P的坐标;若不存在,请说明理由.

更新时间:2021/08/22 12:43:08
|
相似题推荐
解答题-问答题
|
较难
(0.4)
【推荐1】如图,在平面直角坐标系 中,矩形
中,矩形 的顶点
的顶点 、
、 在坐标轴上,点
在坐标轴上,点 的坐标为
的坐标为 点
点 从点
从点 出发,在折线段
出发,在折线段 上以每秒3个单位长度向终点
上以每秒3个单位长度向终点 匀速运动,点
匀速运动,点 从点
从点 出发,在折线段
出发,在折线段 上以每秒4个单位长度向终点
上以每秒4个单位长度向终点 匀速运动.两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接
匀速运动.两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接 .设两点的运动时间为
.设两点的运动时间为 ,线段
,线段 的长度的平方为
的长度的平方为 ,即
,即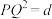 (单位长度2).
(单位长度2).
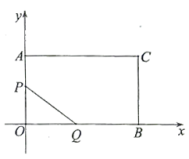
(1)当点 运动到点
运动到点 时,
时, __________
__________ ,当点
,当点 运动到点
运动到点 时,
时, __________
__________ ;
;
(2)求 关于
关于 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量 的取值范围.
的取值范围.
 中,矩形
中,矩形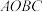 的顶点
的顶点 、
、 在坐标轴上,点
在坐标轴上,点 的坐标为
的坐标为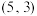 点
点 从点
从点 出发,在折线段
出发,在折线段 上以每秒3个单位长度向终点
上以每秒3个单位长度向终点 匀速运动,点
匀速运动,点 从点
从点 出发,在折线段
出发,在折线段 上以每秒4个单位长度向终点
上以每秒4个单位长度向终点 匀速运动.两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接
匀速运动.两点同时出发,当其中一个点到达终点时,另一个点也停止运动,连接 .设两点的运动时间为
.设两点的运动时间为 ,线段
,线段 的长度的平方为
的长度的平方为 ,即
,即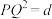 (单位长度2).
(单位长度2).
(1)当点
 运动到点
运动到点 时,
时, __________
__________ ,当点
,当点 运动到点
运动到点 时,
时, __________
__________ ;
;(2)求
 关于
关于 的函数解析式,并直接写出自变量
的函数解析式,并直接写出自变量 的取值范围.
的取值范围.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】如图①,四边形ABCD中,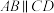 ,
,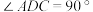 .
.
(1)动点M从A出发,以每秒1个单位的速度沿路线A→B→C→D运动到D停止.设运动时间为t,△AMD的面积为S,S关于t的函数图象如图②所示,则AD= ,CD= ;
(2)在(1)的条件下,当点M在线段BC上运动时,请写出S与t的关系式;
(3)在(1)的条件下,当S=52时,t等于多少?
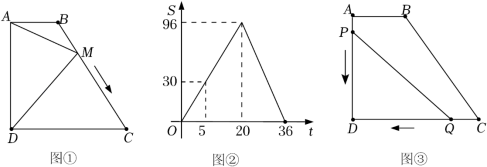
(4)如图③,动点P从点A出发,以每秒2个单位的速度沿路线A→D→C运动到点C停止,同时,动点Q从点C出发,以每秒5个单位的速度沿路线C→D→A运动到点A停止.设运动时间为t,当Q点运动到AD边上时,连接CP、CQ、PQ,当△CPQ的面积为8时,直接写出t的值.
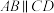 ,
,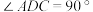 .
.
(1)动点M从A出发,以每秒1个单位的速度沿路线A→B→C→D运动到D停止.设运动时间为t,△AMD的面积为S,S关于t的函数图象如图②所示,则AD= ,CD= ;
(2)在(1)的条件下,当点M在线段BC上运动时,请写出S与t的关系式;
(3)在(1)的条件下,当S=52时,t等于多少?
(4)如图③,动点P从点A出发,以每秒2个单位的速度沿路线A→D→C运动到点C停止,同时,动点Q从点C出发,以每秒5个单位的速度沿路线C→D→A运动到点A停止.设运动时间为t,当Q点运动到AD边上时,连接CP、CQ、PQ,当△CPQ的面积为8时,直接写出t的值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐3】如图①②③,平面内三点O,M,N.如果将线段OM绕点O旋转90°得ON,称点N是点M关于点O的“等直点”,如果OM绕点O顺时针旋转90°得ON,称点N是点M关于点0的“正等直点”,如图②.

(1)如图2,在平面直角坐标系中,已知点P(2,1).
①在 (-1,2),
(-1,2), (2,-1),
(2,-1),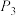 (1,-2)三点中, _________ 是点P关于原点O的“等直点”:
(1,-2)三点中, _________ 是点P关于原点O的“等直点”:
②若直线 :
: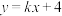 交
交 轴于点M,若点N是直线
轴于点M,若点N是直线 上一点,且点N是点M关于点P的“等直点”,求直线
上一点,且点N是点M关于点P的“等直点”,求直线 的解析式:
的解析式:
(2)如图3,已知点A的坐标为(2,0),点B在直线 :
: 上,若点B关于点A的“正等直点”C在坐标轴上,D是平面内一点,若四边形ABCD是平行四边形,直接写出点D的坐标.
上,若点B关于点A的“正等直点”C在坐标轴上,D是平面内一点,若四边形ABCD是平行四边形,直接写出点D的坐标.
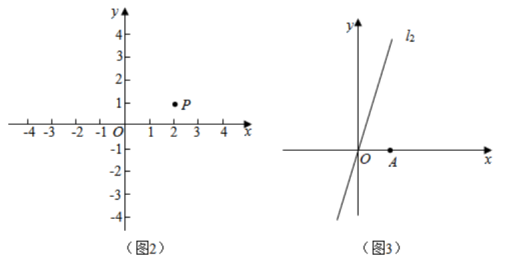

(1)如图2,在平面直角坐标系中,已知点P(2,1).
①在
 (-1,2),
(-1,2), (2,-1),
(2,-1), (1,-2)三点中, _________ 是点P关于原点O的“等直点”:
(1,-2)三点中, _________ 是点P关于原点O的“等直点”:②若直线
 :
: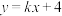 交
交 轴于点M,若点N是直线
轴于点M,若点N是直线 上一点,且点N是点M关于点P的“等直点”,求直线
上一点,且点N是点M关于点P的“等直点”,求直线 的解析式:
的解析式:(2)如图3,已知点A的坐标为(2,0),点B在直线
 :
: 上,若点B关于点A的“正等直点”C在坐标轴上,D是平面内一点,若四边形ABCD是平行四边形,直接写出点D的坐标.
上,若点B关于点A的“正等直点”C在坐标轴上,D是平面内一点,若四边形ABCD是平行四边形,直接写出点D的坐标.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
【推荐1】综合与实践:
在 中,
中, ,
, ,点C在直线l上,点A、B在直线l的同侧,过点A作
,点C在直线l上,点A、B在直线l的同侧,过点A作 于点D.
于点D. .则
.则 与
与 的数量关系是_________________,此时
的数量关系是_________________,此时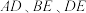 之间的数量关系是_________________.
之间的数量关系是_________________.
(2)探究证明:如图2,在直线l上取点F,使 ,猜想
,猜想 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)拓展延伸:在直线l上任取一点P,连接 ,以点P为直角顶点作等腰直角三角形
,以点P为直角顶点作等腰直角三角形 ,作
,作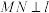 于点N,请直接写出在图3、图4中
于点N,请直接写出在图3、图4中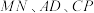 之间的数量关系.
之间的数量关系.
在
 中,
中, ,
, ,点C在直线l上,点A、B在直线l的同侧,过点A作
,点C在直线l上,点A、B在直线l的同侧,过点A作 于点D.
于点D.
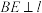 .则
.则 与
与 的数量关系是_________________,此时
的数量关系是_________________,此时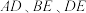 之间的数量关系是_________________.
之间的数量关系是_________________.(2)探究证明:如图2,在直线l上取点F,使
 ,猜想
,猜想 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.(3)拓展延伸:在直线l上任取一点P,连接
 ,以点P为直角顶点作等腰直角三角形
,以点P为直角顶点作等腰直角三角形 ,作
,作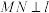 于点N,请直接写出在图3、图4中
于点N,请直接写出在图3、图4中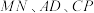 之间的数量关系.
之间的数量关系.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
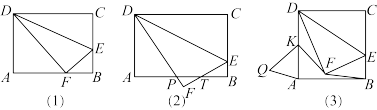
【推荐2】在矩形 中,
中,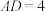 ,E为
,E为 边上一点,将
边上一点,将 沿
沿 折叠得
折叠得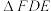 ,
,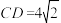 ,点F在
,点F在 边上,求
边上,求 长度;
长度;
(2)如图(2),若点F在矩形 外部,
外部,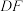 ,
, 分别与
分别与 于点P、T,且
于点P、T,且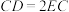 ,
, ,求
,求 长度;
长度;
(3)如图(3),若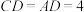 ,取
,取 中点K,作
中点K,作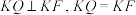 ,当
,当 取最小值时,直接写出
取最小值时,直接写出 长度.
长度.
 中,
中,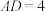 ,E为
,E为 边上一点,将
边上一点,将 沿
沿 折叠得
折叠得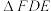 ,
,
 ,点F在
,点F在 边上,求
边上,求 长度;
长度;(2)如图(2),若点F在矩形
 外部,
外部,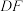 ,
, 分别与
分别与 于点P、T,且
于点P、T,且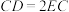 ,
, ,求
,求 长度;
长度;(3)如图(3),若
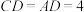 ,取
,取 中点K,作
中点K,作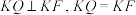 ,当
,当 取最小值时,直接写出
取最小值时,直接写出 长度.
长度.
您最近一年使用:0次

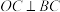 且
且 ,
, ,点C、B按顺时针顺序排列,求B点坐标;
,点C、B按顺时针顺序排列,求B点坐标; ,点A在x轴负半轴上,连
,点A在x轴负半轴上,连 ,作
,作 且
且 ,连
,连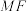 交y轴于N,则ON与AM的数量关系,并证明;
交y轴于N,则ON与AM的数量关系,并证明;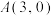 ,
,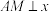 轴,在直线
轴,在直线 上一动点N,连接
上一动点N,连接 并在x轴下方作
并在x轴下方作 且
且 ,连接点
,连接点 与点Q的线段交x轴于点E,当
与点Q的线段交x轴于点E,当 ,则Q点坐标为__________(请同学们自己画图,并直接写出结果)
,则Q点坐标为__________(请同学们自己画图,并直接写出结果)