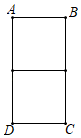
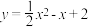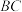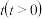如图,某公司用一根长为6m的铝合金型材制作一个“日”字形窗户的框架 ,并且恰好用完整条铝合金型材.设
,并且恰好用完整条铝合金型材.设 的长为xm,矩形
的长为xm,矩形 的面积为ym2.
的面积为ym2.
(1)写出 与
与 的关系式,并指出
的关系式,并指出 的取值范围;
的取值范围;
(2)公司决定将该窗户安装中空玻璃(铝合金型材的宽度忽略不计),已知铝合金型材的价格为80元/m,中空玻璃的价格为110元/m2,当 为多少米时,窗户的造价最大?最大造价是多少?
为多少米时,窗户的造价最大?最大造价是多少?
 ,并且恰好用完整条铝合金型材.设
,并且恰好用完整条铝合金型材.设 的长为xm,矩形
的长为xm,矩形 的面积为ym2.
的面积为ym2.
(1)写出
 与
与 的关系式,并指出
的关系式,并指出 的取值范围;
的取值范围;(2)公司决定将该窗户安装中空玻璃(铝合金型材的宽度忽略不计),已知铝合金型材的价格为80元/m,中空玻璃的价格为110元/m2,当
 为多少米时,窗户的造价最大?最大造价是多少?
为多少米时,窗户的造价最大?最大造价是多少?
更新时间:2022/02/23 09:35:37
|
【知识点】 图形问题(实际问题与二次函数)
相似题推荐
解答题-问答题
|
适中
(0.65)
【推荐1】根据以下素材,探索完成任务
| 如何设计纸盒 | ||
| 素材1 | 利用一边长为40cm的正方形纸板可能设计成如图1和图2所示的两种纸盒,图1是无盖的纸盒,图2是一个有盖的纸盒. |  |
| 素材2 | 如图,若在正方形硬纸板的四角各剪掉一个同样大小的小正方形,将剩余部分折成一个无盖的长方体盒子。 | 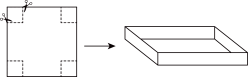 |
问题解决 | ||
| 任务1 | 初步探究:折一个底面积为 无盖长方体盒子 无盖长方体盒子 | 求剪掉的小正方形的边长为多少? |
| 任务2 | 探究折成的无盖长方体盒子的侧面积是否有最大值? | 如果有,求出这个最大值和此时剪掉的小正方形的边长;如果没有,说明理由 |
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐2】如图,下面是某同学在平面直角坐标系中设计的一动画示意图,点A,N在x轴上,在 上方有五个水平台阶
上方有五个水平台阶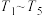 (各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶
(各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶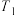 到x轴的距离为10.从点A处向右上方沿抛物线
到x轴的距离为10.从点A处向右上方沿抛物线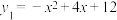 发出一个带光的点P.
发出一个带光的点P.
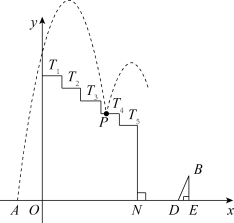
(1)点P恰好落在台阶 上,求此时落点P的坐标;
上,求此时落点P的坐标;
(2)当点P落到台阶 上后立即向右弹起,又形成了另一条与原抛物线形状相同的新抛物线
上后立即向右弹起,又形成了另一条与原抛物线形状相同的新抛物线 ,且最大高度为11,求新抛物线
,且最大高度为11,求新抛物线 的表达式;
的表达式;
(3)如图,在x轴上摆放一个可以左右平移的 ,且直角边
,且直角边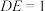 ,
, .若保证(2)中沿抛物线
.若保证(2)中沿抛物线 下落的点P必须落在斜边
下落的点P必须落在斜边 (包括端点)上,则点B横坐标的最大值比最小值大多少?
(包括端点)上,则点B横坐标的最大值比最小值大多少?
 上方有五个水平台阶
上方有五个水平台阶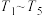 (各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶
(各拐角均为90°),每个台阶的高、宽分别是1和1.5,台阶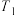 到x轴的距离为10.从点A处向右上方沿抛物线
到x轴的距离为10.从点A处向右上方沿抛物线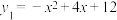 发出一个带光的点P.
发出一个带光的点P.
(1)点P恰好落在台阶
 上,求此时落点P的坐标;
上,求此时落点P的坐标;(2)当点P落到台阶
 上后立即向右弹起,又形成了另一条与原抛物线形状相同的新抛物线
上后立即向右弹起,又形成了另一条与原抛物线形状相同的新抛物线 ,且最大高度为11,求新抛物线
,且最大高度为11,求新抛物线 的表达式;
的表达式;(3)如图,在x轴上摆放一个可以左右平移的
 ,且直角边
,且直角边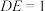 ,
, .若保证(2)中沿抛物线
.若保证(2)中沿抛物线 下落的点P必须落在斜边
下落的点P必须落在斜边 (包括端点)上,则点B横坐标的最大值比最小值大多少?
(包括端点)上,则点B横坐标的最大值比最小值大多少?
您最近一年使用:0次