名校
解题方法
1 . 通过研究,已知对任意平面向量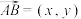 ,把
,把 绕其起点A沿逆时针方向旋转
绕其起点A沿逆时针方向旋转 角得到向量
角得到向量 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 角得到点P,
角得到点P,
(1)已知平面内点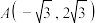 ,点
,点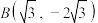 ,把点B绕点A逆时针旋转
,把点B绕点A逆时针旋转 得到点P,求点P的坐标:
得到点P,求点P的坐标:
(2)已知二次方程 的图像是由平面直角坐标系下某标准椭圆
的图像是由平面直角坐标系下某标准椭圆 绕原点O逆时针旋转
绕原点O逆时针旋转 所得的斜椭圆C,
所得的斜椭圆C,
(i)求斜椭圆C的离心率;
(ⅱ)过点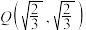 作与两坐标轴都不平行的直线
作与两坐标轴都不平行的直线 交斜椭圆C于点M、N,过原点O作直线
交斜椭圆C于点M、N,过原点O作直线 与直线
与直线 垂直,直线
垂直,直线 交斜椭圆C于点G、H,判断
交斜椭圆C于点G、H,判断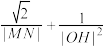 是否为定值,若是,请求出定值,若不是,请说明理由.
是否为定值,若是,请求出定值,若不是,请说明理由.
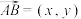 ,把
,把 绕其起点A沿逆时针方向旋转
绕其起点A沿逆时针方向旋转 角得到向量
角得到向量 ,叫做把点B绕点A逆时针方向旋转
,叫做把点B绕点A逆时针方向旋转 角得到点P,
角得到点P,(1)已知平面内点
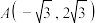 ,点
,点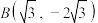 ,把点B绕点A逆时针旋转
,把点B绕点A逆时针旋转 得到点P,求点P的坐标:
得到点P,求点P的坐标:(2)已知二次方程
 的图像是由平面直角坐标系下某标准椭圆
的图像是由平面直角坐标系下某标准椭圆 绕原点O逆时针旋转
绕原点O逆时针旋转 所得的斜椭圆C,
所得的斜椭圆C,(i)求斜椭圆C的离心率;
(ⅱ)过点
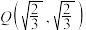 作与两坐标轴都不平行的直线
作与两坐标轴都不平行的直线 交斜椭圆C于点M、N,过原点O作直线
交斜椭圆C于点M、N,过原点O作直线 与直线
与直线 垂直,直线
垂直,直线 交斜椭圆C于点G、H,判断
交斜椭圆C于点G、H,判断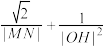 是否为定值,若是,请求出定值,若不是,请说明理由.
是否为定值,若是,请求出定值,若不是,请说明理由.
您最近一年使用:0次
2024-07-02更新
|
1036次组卷
|
11卷引用:四川省新高考联盟校级2025届高三九月适应考数学试题
四川省新高考联盟校级2025届高三九月适应考数学试题江西省新余市2023-2024学年高三第二次模拟考试数学试题(已下线)专题11 解析几何中的定值问题【练】(压轴大全)(已下线)专题20 创新定义题型(2大考向真题解读)(已下线)椭圆01-一轮复习考点专练(已下线)专题5 解析几何中的新定义压轴大题(二)【讲】重庆市鲁能巴蜀中学校2024-2025学年高二(荣耀班)上学期入学考试数学试题A卷(已下线)拔高点突破03 圆锥曲线背景下的新定义问题(八大题型)(已下线)专题3 函数思想 确定定值(经典好题母题)【练】(已下线)第8题 斜椭圆求离心率(高三备考10月刊)福建省厦门双十中学2024-2025学年高二上学期期中考试数学试题
2 . 已知抛物线 :
: 的焦点为
的焦点为 ,过点
,过点 的直线与
的直线与 相交于点
相交于点 ,
, ,
, 面积的最小值为
面积的最小值为 (
( 为坐标原点).按照如下方式依次构造点
为坐标原点).按照如下方式依次构造点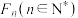 :
: 的坐标为
的坐标为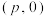 ,直线
,直线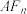 ,
,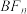 与
与 的另一个交点分别为
的另一个交点分别为 ,
, ,直线
,直线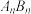 与
与 轴的交点为
轴的交点为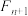 ,设点
,设点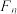 的横坐标为
的横坐标为 .
.
(1)求 的值;
的值;
(2)求数列 的通项公式;
的通项公式;
(3)数列 中,是否存在连续三项(按原顺序)构成等差数列?若存在,指出所有这样的连续三项;若不存在,请说明理由.
中,是否存在连续三项(按原顺序)构成等差数列?若存在,指出所有这样的连续三项;若不存在,请说明理由.
 :
: 的焦点为
的焦点为 ,过点
,过点 的直线与
的直线与 相交于点
相交于点 ,
, ,
, 面积的最小值为
面积的最小值为 (
( 为坐标原点).按照如下方式依次构造点
为坐标原点).按照如下方式依次构造点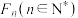 :
: 的坐标为
的坐标为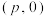 ,直线
,直线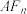 ,
,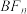 与
与 的另一个交点分别为
的另一个交点分别为 ,
, ,直线
,直线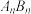 与
与 轴的交点为
轴的交点为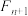 ,设点
,设点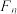 的横坐标为
的横坐标为 .
.(1)求
 的值;
的值;(2)求数列
 的通项公式;
的通项公式;(3)数列
 中,是否存在连续三项(按原顺序)构成等差数列?若存在,指出所有这样的连续三项;若不存在,请说明理由.
中,是否存在连续三项(按原顺序)构成等差数列?若存在,指出所有这样的连续三项;若不存在,请说明理由.
您最近一年使用:0次
2024-09-05更新
|
647次组卷
|
3卷引用:四川省大数据精准教学联盟2025届高三上学期一模考试数学试题
名校
解题方法
3 . 已知双曲线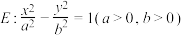 的实轴长为2,顶点到渐近线的距离为
的实轴长为2,顶点到渐近线的距离为 .
.
(1)求双曲线 的标准方程;
的标准方程;
(2)若直线 与
与 的右支及渐近线的交点自上而下依次为
的右支及渐近线的交点自上而下依次为 ,证明:
,证明: ;
;
(3)求二元二次方程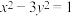 的正整数解
的正整数解 ,可先找到初始解
,可先找到初始解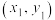 ,其中
,其中 为所有解
为所有解 中的最小值,因为
中的最小值,因为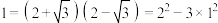 ,所以
,所以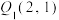 ;因为
;因为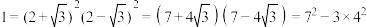 ,所以
,所以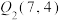 ;重复上述过程,因为
;重复上述过程,因为 与
与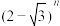 的展开式中,不含
的展开式中,不含 的部分相等,含
的部分相等,含 的部分互为相反数,故可设
的部分互为相反数,故可设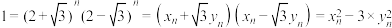 ,所以
,所以 .若方程
.若方程 的正整数解为
的正整数解为 ,且初始解
,且初始解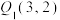 ,则
,则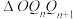 的面积是否为定值?若是,请求出该定值,并说明理由.
的面积是否为定值?若是,请求出该定值,并说明理由.
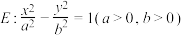 的实轴长为2,顶点到渐近线的距离为
的实轴长为2,顶点到渐近线的距离为 .
.(1)求双曲线
 的标准方程;
的标准方程;(2)若直线
 与
与 的右支及渐近线的交点自上而下依次为
的右支及渐近线的交点自上而下依次为 ,证明:
,证明: ;
;(3)求二元二次方程
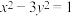 的正整数解
的正整数解 ,可先找到初始解
,可先找到初始解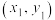 ,其中
,其中 为所有解
为所有解 中的最小值,因为
中的最小值,因为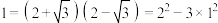 ,所以
,所以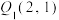 ;因为
;因为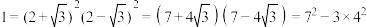 ,所以
,所以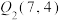 ;重复上述过程,因为
;重复上述过程,因为 与
与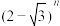 的展开式中,不含
的展开式中,不含 的部分相等,含
的部分相等,含 的部分互为相反数,故可设
的部分互为相反数,故可设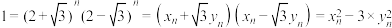 ,所以
,所以 .若方程
.若方程 的正整数解为
的正整数解为 ,且初始解
,且初始解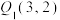 ,则
,则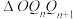 的面积是否为定值?若是,请求出该定值,并说明理由.
的面积是否为定值?若是,请求出该定值,并说明理由.
您最近一年使用:0次
2024-09-17更新
|
526次组卷
|
4卷引用:四川省成都列五中学2024-2025学年高三上学期9月月考数学试题
四川省成都列五中学2024-2025学年高三上学期9月月考数学试题广西南宁市第三中学2025届高三上学期9月适应性测试数学试题(已下线)阶段测6周测14-周测18【实战演练】提升卷安徽省蚌埠市五河第一中学2024-2025学年高二上学期期中考试数学试题
名校
解题方法
4 . 定义:由椭圆的两个焦点和短轴的一个端点组成的三角形称为该椭圆的“特征三角形”.若两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将“特征三角形”的相似比称为椭圆的相似比.已知椭圆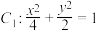 ,椭圆
,椭圆 与
与 是“相似椭圆”,已知椭圆
是“相似椭圆”,已知椭圆 的短半轴长为
的短半轴长为 .
.
(1)写出椭圆 的方程(用
的方程(用 表示);
表示);
(2)若椭圆 的焦点在
的焦点在 轴上,且
轴上,且 上存在两点
上存在两点 ,
, 关于直线
关于直线 对称,求实数
对称,求实数 的取值范围.
的取值范围.
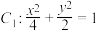 ,椭圆
,椭圆 与
与 是“相似椭圆”,已知椭圆
是“相似椭圆”,已知椭圆 的短半轴长为
的短半轴长为 .
.(1)写出椭圆
 的方程(用
的方程(用 表示);
表示);(2)若椭圆
 的焦点在
的焦点在 轴上,且
轴上,且 上存在两点
上存在两点 ,
, 关于直线
关于直线 对称,求实数
对称,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2021-05-21更新
|
627次组卷
|
2卷引用:四川省绵阳市南山中学2021届高三高考适应性考试(二)数学(文)试题



