名校
解题方法
1 . 设m,n是两条不同的直线,α,β是两个不同的平面( )
A.若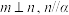 ,则 ,则 | B.若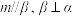 ,则 ,则 |
C.若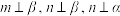 ,则 ,则 | D.若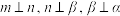 ,则 ,则 . . |
您最近一年使用:0次
7日内更新
|
313次组卷
|
67卷引用:【全国百强校】陕西省西安市长安区第一中学2017-2018学年高一下学期期末考试数学试题1
【全国百强校】陕西省西安市长安区第一中学2017-2018学年高一下学期期末考试数学试题1【全国百强校】陕西省西安市长安区第一中学2017-2018学年高一下学期期末考试数学试题2陕西省西安工业大学附属中学2022-2023学年高一下学期第二次月考数学试题陕西省西安市大联考2022-2023学年高一下学期期中数学试题2015届甘肃省天水市一中高三5月中旬仿真考试文科数学试卷2015-2016学年江西省上高县二中高二上学期第一次月考数学试卷2015-2016学年内蒙古赤峰市宁城县高一上学期期末考试数学试卷2015-2016学年西藏日喀则一中高一4月月考数学试卷2016-2017学年广东清远三中高二文上学期月考三数学试卷四川省三台中学2016-2017学年高一下学期第三次月考(6月)数学试题人教A版高中数学必修二模块质量评估(A卷)【全国百强校】北京市人大附中2018届高三5月考前热身练习(三模)数学文科试题【全国百强校】黑龙江省大庆实验中学2017-2018学年高一6月月考数学(文)试题北京市人大附中2018届高三下学期三模考试数学(文科)试题【市级联考】安徽省蚌埠市2018-2019学年高二上学期期末学业水平检测数学(理)试题内蒙古赤峰市2018-2019学年高一下学期期末数学(理)试题河北省承德市第一中学2019-2020学年高三上学期12月月考数学(理)试题(已下线)【新东方】杭州高二数学试卷246浙江省“七彩阳光”新高考研究联盟2019-2020学年高二上学期期中联考数学试题(已下线)【新东方】杭州高二数学试卷247(已下线)2020届高三12月第02期(考点07)(理科)-《新题速递·数学》安徽省芜湖市2019-2020学年高二上学期期末数学(文)试题2020届北京市第十一中学高三一模数学试题2019年浙江省普通高中学业水平冲A卷(一)(已下线)专题23 空间点线面的位置关系-十年(2011-2020)高考真题数学分项北京市首都师范大学附属中学2020-2021学年高二上学期数学期中考试试题(已下线)专题8.5 直线、平面垂直的判定及性质 (精练)-2021年高考数学(文)一轮复习讲练测福建省2021届普通高中学业水平合格性考试(会考 )适应性练习数学试卷三试题浙江省宁波市慈溪市2020-2021学年高二上学期期末数学试题浙江省金华市磐安县第二中学2020-2021学年高二上学期期中数学试题山西省运城市东康一中2019-2020学年高二上学期中段考试数学试题安徽省滁州市定远县育才学校2020-2021学年高一下学期期末数学试题(已下线)专题07 空间向量与立体几何-十年(2012-2021)高考数学真题分项汇编(浙江专用)黑龙江省大庆铁人中学2021-2022学年高三上学期期中考试理科数学试题黑龙江省大庆铁人中学2021-2022学年高三上学期期中考试文科数学试题(已下线)8.6.4空间直线、平面的垂直(4)(课后作业)【师说智慧课堂】新教材人教A(2019)必修(第二册)山西省运城市2021~2022学年高一下学期5月阶段性检测数学试题河北省唐山市2021-2022学年高一下学期期末数学试题(已下线)专题23 空间中的垂直关系(讲义)-2023年高考数学一轮复习精讲精练宝典(新高考专用)(已下线)专题31 直线、平面垂直的判定与性质-1内蒙古自治区赤峰市红山区2022-2023学年高二上学期期末数学文科试题甘肃省兰州市第五十八中学2022-2023学年高三下学期第二次模拟考试数学(理科)试卷(已下线)高一下数学期中模拟卷02(必修二前三章)-【单元测试】2022-2023学年高一数学分层训练AB卷(人教A版2019必修第二册)湖北省武汉市第一中学2022-2023学年高一下学期5月月考数学试题(已下线)高一下学期期末考点大通关真题精选100题(2)-期中期末考点大串讲湖南省长沙市长郡中学2022-2023学年高二下学期期末数学试题安徽省蚌埠市2022-2023学年高一下学期期末学业水平监测数学试题四川省宜宾市宜宾市第四中学校2022-2023学年高一下学期期末数学试题江西省萍乡市安源中学2022-2023学年高一下学期期末质量检测数学试题江西省宜春市第十中学2024届高二上学期开学检测数学试题四川省泸县第四中学2023-2024学年高二上学期开学数学试题江苏省常州高级中学2024届高三上学期期初检测数学试题四川省蓬溪中学校2023-2024学年高二上学期第一次质量检测数学试题北京市第五中学2024届高三上学期10月月考数学试题贵州省贵阳市观山湖区第一高级中学2023-2024学年高二上学期9月月考数学试题(已下线)第04讲 直线、平面垂直的判定与性质(五大题型)(讲义)(已下线)第七章 综合测试A(基础卷)河南省三门峡市陕州中学2024届高三上学期第三次月清数学试题(已下线)2024年全国高考名校名师联席命制数学(理)信息卷(八)北京市第八十中学2023-2024学年高三上学期10月月考数学试卷广西部分学校2024届高三下学期开学考试数学试题(已下线)专题13 立体几何选择题(文科)-2(已下线)第八章:立体几何初步章末重点题型复习(1)-同步精品课堂(人教A版2019必修第二册)(已下线)专题04空间点、直线、平面的位置关系与空间直线、平面的平行-期末真题分类汇编(新高考专用)上海市实验学校2024-2025学年高二上学期10月月考数学试卷(已下线)阶段测6 周测14-周测18 (一轮好卷北京专版 )北京市海淀区北京交通大学附属中学2024-2025学年高二上学期11月期中练习数学试题
2 . 已知 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
 、
、 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )A.若 , , ,则 ,则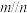 | B.若 , , ,则 ,则 |
C.若 , ,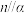 ,则 ,则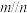 | D.若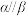 , , ,则 ,则 |
您最近一年使用:0次
2024-11-01更新
|
548次组卷
|
5卷引用:陕西省榆林市第十中学2022-2023学年高三第五次模拟考试理科数学试题
陕西省榆林市第十中学2022-2023学年高三第五次模拟考试理科数学试题陕西省榆林市第十中学2022-2023学年高三第五次模拟考试文科数学试题贵州省铜仁市松桃苗族自治县第三高级中学2024-2025学年高二上学期10月月考数学试题(已下线)第五节直线、平面垂直的判定与性质【同步课时】提升卷(已下线)第三节 直线、平面平行的判定与性质【同步课时】北京专项
解题方法
3 . 在正方体 中,E,F分别为
中,E,F分别为 ,
, 的中点,则直线
的中点,则直线 与
与 所成的角为( )
所成的角为( )
 中,E,F分别为
中,E,F分别为 ,
, 的中点,则直线
的中点,则直线 与
与 所成的角为( )
所成的角为( )A. | B. | C. | D. |
您最近一年使用:0次
2024-11-01更新
|
234次组卷
|
3卷引用:陕西省榆林市第十中学2022-2023学年高三第五次模拟考试理科数学试题
陕西省榆林市第十中学2022-2023学年高三第五次模拟考试理科数学试题云南省昆明市西南联大研究院附属学校2024-2025学年高二上学期10月月考数学试卷(已下线)第二节 空间点、直线、平面之间的位置关系【讲】北京专版
4 . 下列命题:①若直线在 轴,
轴, 轴上的截距分别为
轴上的截距分别为 ,则方程可记为
,则方程可记为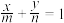 ;②若直线
;②若直线 与直线
与直线 垂直,则它们的斜率乘积为
垂直,则它们的斜率乘积为 ;③若
;③若 表示不同的直线,
表示不同的直线, 表示平面,满足
表示平面,满足 则
则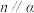 ;④若
;④若 表示不同的直线,
表示不同的直线, 表示不同平面,高足
表示不同平面,高足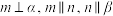 ,则
,则 .以上命题正面的个数为( )
.以上命题正面的个数为( )
 轴,
轴, 轴上的截距分别为
轴上的截距分别为 ,则方程可记为
,则方程可记为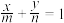 ;②若直线
;②若直线 与直线
与直线 垂直,则它们的斜率乘积为
垂直,则它们的斜率乘积为 ;③若
;③若 表示不同的直线,
表示不同的直线, 表示平面,满足
表示平面,满足 则
则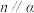 ;④若
;④若 表示不同的直线,
表示不同的直线, 表示不同平面,高足
表示不同平面,高足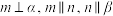 ,则
,则 .以上命题正面的个数为( )
.以上命题正面的个数为( )| A.0 | B.1 | C.2 | D.3 |
您最近一年使用:0次
解题方法
5 . 如图,正方体 的棱长为2,线段
的棱长为2,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,以下结论错误的是( )
,以下结论错误的是( )
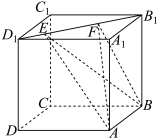
 的棱长为2,线段
的棱长为2,线段 上有两个动点E,F,且
上有两个动点E,F,且 ,以下结论错误的是( )
,以下结论错误的是( )
A.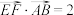 |
B.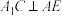 |
C.异面直线 , , 所成的角为定值 所成的角为定值 |
D.正方体 的体积是三棱锥 的体积是三棱锥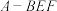 的体积的12倍 的体积的12倍 |
您最近一年使用:0次
名校
6 . 以下四个命题正确的有( )
| A.三个平面最多可以把空间分成八部分 |
B.若直线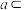 平面 平面 ,直线 ,直线 平面 平面 ,则“ ,则“ 与 与 相交”等价于“ 相交”等价于“ 与 与 相交” 相交” |
C.若直线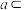 平面 平面 ,直线 ,直线 平面 平面 ,且 ,且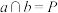 , , ,则 ,则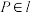 |
| D.若四条直线中任意两条共面,则这四条直线共面 |
您最近一年使用:0次
2024-10-23更新
|
153次组卷
|
3卷引用:陕西省咸阳市乾县晨光中学2024-2025学年高二上学期10月阶段检测数学试卷
名校
解题方法
7 . 设 是不同的直线,
是不同的直线, 是不同的平面,下列说法正确的是( )
是不同的平面,下列说法正确的是( )
 是不同的直线,
是不同的直线, 是不同的平面,下列说法正确的是( )
是不同的平面,下列说法正确的是( )A.若 ,则 ,则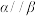 | B.若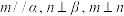 ,则 ,则 |
C.若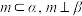 ,则 ,则 | D.若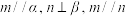 ,则 ,则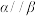 |
您最近一年使用:0次
2024-10-23更新
|
286次组卷
|
8卷引用:陕西省宝鸡市宝鸡中学2024-2025学年高二上学期阶段考试(一)(10月)数学试题
陕西省宝鸡市宝鸡中学2024-2025学年高二上学期阶段考试(一)(10月)数学试题安徽省宿州市泗县第一中学2020届高三下学期最后一卷数学(文)试题(已下线)练习15+直线、平面平行的判定与性质-2020-2021学年【补习教材·寒假作业】高一数学(北师大版)(已下线)【新东方】高中数学20210429—004【2020】【高二上】(已下线)13.2.4平面与平面位置关系(3)面面垂直判定与性质(备作业)-【上好课】2021-2022学年高一数学同步备课系列(苏教版2019必修第二册)(已下线)8.5.3 平面与平面平行 (第1课时) 平面与平面平行的判定(分层作业)-【上好课】(已下线)数学(广东专用)-新高二上学期数学开学摸底考试卷(已下线)第三节空间点、直线、平面的位置关系【同步课时】基础卷
解题方法
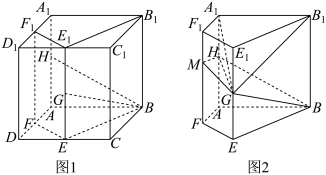
8 . 图1是棱长为2的正方体 ,
, ,
, ,
, ,
, 分别是
分别是 ,
, ,
, ,
, 的中点,截去三棱柱
的中点,截去三棱柱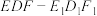 和三棱柱
和三棱柱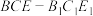 得到如图2的四棱柱
得到如图2的四棱柱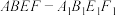 ,
, ,
, 分别是
分别是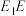 ,
,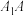 的中点,过点
的中点,过点 ,
, ,
, 的平面
的平面 交
交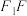 于点
于点 .
. 的长;
的长;
(2)求平面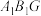 与平面
与平面 夹角的余弦值.
夹角的余弦值.
 ,
, ,
, ,
, ,
, 分别是
分别是 ,
, ,
, ,
, 的中点,截去三棱柱
的中点,截去三棱柱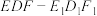 和三棱柱
和三棱柱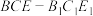 得到如图2的四棱柱
得到如图2的四棱柱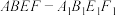 ,
, ,
, 分别是
分别是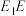 ,
,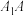 的中点,过点
的中点,过点 ,
, ,
, 的平面
的平面 交
交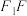 于点
于点 .
.
 的长;
的长;(2)求平面
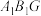 与平面
与平面 夹角的余弦值.
夹角的余弦值.
您最近一年使用:0次
2024-10-15更新
|
71次组卷
|
2卷引用:陕西省咸阳市乾县第二中学2024-2025学年高二上学期10月阶段检测数学试卷
解题方法
9 . 如图,将正方形 沿对角线
沿对角线 折起,并使得平面
折起,并使得平面 垂直于平面
垂直于平面 ,若取图中相关线段的中点进行转化,则可求得直线
,若取图中相关线段的中点进行转化,则可求得直线 与
与 所成的角为( )
所成的角为( )
 沿对角线
沿对角线 折起,并使得平面
折起,并使得平面 垂直于平面
垂直于平面 ,若取图中相关线段的中点进行转化,则可求得直线
,若取图中相关线段的中点进行转化,则可求得直线 与
与 所成的角为( )
所成的角为( ) 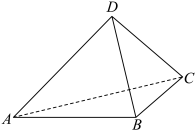
| A.90° | B.60° | C.45° | D.30° |
您最近一年使用:0次
名校
解题方法
10 . 如图,在正方形 中,异面直线
中,异面直线 与
与 所成的角是( )
所成的角是( )
 中,异面直线
中,异面直线 与
与 所成的角是( )
所成的角是( )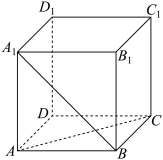
| A.120° | B.90° | C.60° | D.30° |
您最近一年使用:0次



