解题方法
1 . 已知椭圆C: 的焦点和上顶点分别为
的焦点和上顶点分别为 、
、 、B,我们称
、B,我们称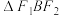 为椭圆C的特征三角形,如果两个椭圆的特征三角形是相似三角形,则称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为“相似椭圆”的相似比.已知椭圆
为椭圆C的特征三角形,如果两个椭圆的特征三角形是相似三角形,则称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为“相似椭圆”的相似比.已知椭圆 :
: 以抛物线
以抛物线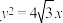 的焦点为一个焦点,且椭圆上任意一点到两焦点的距离之和为4.
的焦点为一个焦点,且椭圆上任意一点到两焦点的距离之和为4.
(1)若椭圆 与椭圆
与椭圆 相似,且相似比为2,求椭圆
相似,且相似比为2,求椭圆 的方程;
的方程;
(2)已知点 ,点A是椭圆
,点A是椭圆 上的任意一点,点B是点A关于原点的对称点.记
上的任意一点,点B是点A关于原点的对称点.记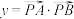 ,求y的取值范围;
,求y的取值范围;
(3)已知直线l:y=x+1,与椭圆 相似且短半轴长为b的椭圆为
相似且短半轴长为b的椭圆为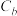 ,是否存在这样的b,使得椭圆
,是否存在这样的b,使得椭圆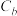 上存在两点M、N关于直线l对称,若存在,请求出b的范围;若不存在,请说明理由.
上存在两点M、N关于直线l对称,若存在,请求出b的范围;若不存在,请说明理由.
 的焦点和上顶点分别为
的焦点和上顶点分别为 、
、 、B,我们称
、B,我们称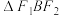 为椭圆C的特征三角形,如果两个椭圆的特征三角形是相似三角形,则称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为“相似椭圆”的相似比.已知椭圆
为椭圆C的特征三角形,如果两个椭圆的特征三角形是相似三角形,则称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为“相似椭圆”的相似比.已知椭圆 :
: 以抛物线
以抛物线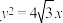 的焦点为一个焦点,且椭圆上任意一点到两焦点的距离之和为4.
的焦点为一个焦点,且椭圆上任意一点到两焦点的距离之和为4.(1)若椭圆
 与椭圆
与椭圆 相似,且相似比为2,求椭圆
相似,且相似比为2,求椭圆 的方程;
的方程;(2)已知点
 ,点A是椭圆
,点A是椭圆 上的任意一点,点B是点A关于原点的对称点.记
上的任意一点,点B是点A关于原点的对称点.记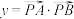 ,求y的取值范围;
,求y的取值范围;(3)已知直线l:y=x+1,与椭圆
 相似且短半轴长为b的椭圆为
相似且短半轴长为b的椭圆为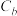 ,是否存在这样的b,使得椭圆
,是否存在这样的b,使得椭圆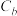 上存在两点M、N关于直线l对称,若存在,请求出b的范围;若不存在,请说明理由.
上存在两点M、N关于直线l对称,若存在,请求出b的范围;若不存在,请说明理由.
您最近一年使用:0次



