1 . 如图所示,两个不同的平面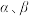 ,A、B两点在两平面的交线上,
,A、B两点在两平面的交线上, ,以AB为直径的圆
,以AB为直径的圆 在平面
在平面 内,以AB为长轴,F、
内,以AB为长轴,F、 为焦点的椭圆
为焦点的椭圆 在平面
在平面 内.过圆
内.过圆 上一点P向平面
上一点P向平面 作垂线,垂足为H,已知
作垂线,垂足为H,已知 ,且
,且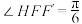 .若射线FH与椭圆相交于点Q,且
.若射线FH与椭圆相交于点Q,且 ,在平面
,在平面 内,以点H为圆心,半径为4的圆经过点Q,且圆H与直线AB相切.则平面
内,以点H为圆心,半径为4的圆经过点Q,且圆H与直线AB相切.则平面 所成的角的余弦值为( )
所成的角的余弦值为( )
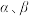 ,A、B两点在两平面的交线上,
,A、B两点在两平面的交线上, ,以AB为直径的圆
,以AB为直径的圆 在平面
在平面 内,以AB为长轴,F、
内,以AB为长轴,F、 为焦点的椭圆
为焦点的椭圆 在平面
在平面 内.过圆
内.过圆 上一点P向平面
上一点P向平面 作垂线,垂足为H,已知
作垂线,垂足为H,已知 ,且
,且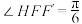 .若射线FH与椭圆相交于点Q,且
.若射线FH与椭圆相交于点Q,且 ,在平面
,在平面 内,以点H为圆心,半径为4的圆经过点Q,且圆H与直线AB相切.则平面
内,以点H为圆心,半径为4的圆经过点Q,且圆H与直线AB相切.则平面 所成的角的余弦值为( )
所成的角的余弦值为( )
A. | B.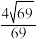 |
C. | D.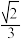 |
您最近一年使用:0次
2023-12-21更新
|
298次组卷
|
3卷引用:湖北省云学名校联盟2023-2024学年高二上学期12月联考数学试题
名校
2 . 已知点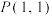 为椭圆
为椭圆 :
: (
( )内一点,过点
)内一点,过点 的直线
的直线 与
与 交于
交于 两点.当直线
两点.当直线 经过
经过 的右焦点
的右焦点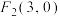 时,点
时,点 恰好为线段
恰好为线段 的中点.
的中点.
(1)求椭圆 的方程;
的方程;
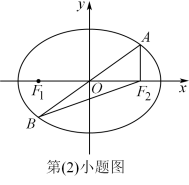
(2)椭圆的光学性质是指:从椭圆的一个焦点出发的一束光线经椭圆反射后会经过椭圆的另一个焦点.设从椭圆 的左焦点
的左焦点 出发的一束光线经过点
出发的一束光线经过点 ,被直线
,被直线 反射,反射后的光线经过椭圆二次反射后恰好经过点
反射,反射后的光线经过椭圆二次反射后恰好经过点 ,由此形成的三角形称之为“光线三角形”.求此时直线
,由此形成的三角形称之为“光线三角形”.求此时直线 的方程,并计算“光线三角形”的周长.
的方程,并计算“光线三角形”的周长.
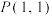 为椭圆
为椭圆 :
: (
( )内一点,过点
)内一点,过点 的直线
的直线 与
与 交于
交于 两点.当直线
两点.当直线 经过
经过 的右焦点
的右焦点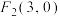 时,点
时,点 恰好为线段
恰好为线段 的中点.
的中点.(1)求椭圆
 的方程;
的方程;(2)椭圆的光学性质是指:从椭圆的一个焦点出发的一束光线经椭圆反射后会经过椭圆的另一个焦点.设从椭圆
 的左焦点
的左焦点 出发的一束光线经过点
出发的一束光线经过点 ,被直线
,被直线 反射,反射后的光线经过椭圆二次反射后恰好经过点
反射,反射后的光线经过椭圆二次反射后恰好经过点 ,由此形成的三角形称之为“光线三角形”.求此时直线
,由此形成的三角形称之为“光线三角形”.求此时直线 的方程,并计算“光线三角形”的周长.
的方程,并计算“光线三角形”的周长.
您最近一年使用:0次
2023-11-06更新
|
580次组卷
|
4卷引用:湖北省部分县市重点中学温德克英名校联盟2023-2024学年高二上学期11月期中综合性质量监测数学试卷
湖北省部分县市重点中学温德克英名校联盟2023-2024学年高二上学期11月期中综合性质量监测数学试卷广东省佛山市顺德区普通高中2024届高三上学期教学质量检测(一)数学试题重庆市九龙坡区重庆外国语学校2024届高三上学期12月月考数学试题(已下线)拔高点突破02 圆锥曲线中的仿射变换、非对称韦达、光学性质问题(五大题型)
名校
解题方法
3 . 在xoy坐标平面内,已知椭圆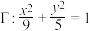 的左、右焦点分别为
的左、右焦点分别为 、
、 ,直线
,直线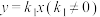 与
与 相交于A、B两点.
相交于A、B两点.
(1)记d为A到直线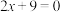 的距离,当
的距离,当 变化时,求证:
变化时,求证: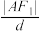 为定值;
为定值;
(2)当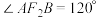 时,求
时,求 的值;
的值;
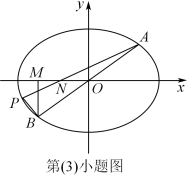
(3)过B作BM⊥x轴,垂足为M,OM的中点为N,延长AN交 于另一点P,记直线PB的斜率为
于另一点P,记直线PB的斜率为 ,当
,当 取何值时,
取何值时,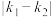 有最小值?并求出此最小值.
有最小值?并求出此最小值.
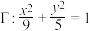 的左、右焦点分别为
的左、右焦点分别为 、
、 ,直线
,直线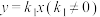 与
与 相交于A、B两点.
相交于A、B两点.

(1)记d为A到直线
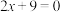 的距离,当
的距离,当 变化时,求证:
变化时,求证: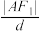 为定值;
为定值;(2)当
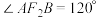 时,求
时,求 的值;
的值;(3)过B作BM⊥x轴,垂足为M,OM的中点为N,延长AN交
 于另一点P,记直线PB的斜率为
于另一点P,记直线PB的斜率为 ,当
,当 取何值时,
取何值时,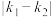 有最小值?并求出此最小值.
有最小值?并求出此最小值.
您最近一年使用:0次
2022-12-15更新
|
870次组卷
|
2卷引用:湖北省襄阳市第四中学2022-2023学年高二上学期第三次月考数学试题
名校
解题方法
4 . 下列说法错误的是( )
A.“ ”是“直线 ”是“直线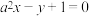 与直线 与直线 互相垂直”的充要条件 互相垂直”的充要条件 |
B.若点 是曲线 是曲线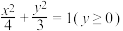 上的动点,则 上的动点,则 的取值范围是 的取值范围是 |
C.已知双曲线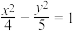 左焦点为 左焦点为 , , 是左支上一动点,则 是左支上一动点,则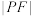 的最小值是 的最小值是 |
D.已知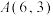 , , , , 是椭圆 是椭圆 : :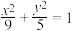 的左右焦点, 的左右焦点, 是椭圆 是椭圆 上的一动点,则 上的一动点,则 的最小值是 的最小值是 |
您最近一年使用:0次
2022-11-24更新
|
561次组卷
|
3卷引用:湖北省襄阳市第五中学2022-2023学年高二上学期12月月考数学试题
名校
5 . (多选)已知在平面直角坐标系中,点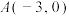 ,
,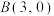 ,点P为一动点,且
,点P为一动点,且 ,则下列说法中正确的是( )
,则下列说法中正确的是( )
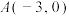 ,
,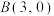 ,点P为一动点,且
,点P为一动点,且 ,则下列说法中正确的是( )
,则下列说法中正确的是( )A.当 时,点P的轨迹不存在 时,点P的轨迹不存在 |
B.当 时,点P的轨迹是椭圆,且焦距为3 时,点P的轨迹是椭圆,且焦距为3 |
C.当 时,点P的轨迹是椭圆,且焦距为6 时,点P的轨迹是椭圆,且焦距为6 |
D.当 时,点P的轨迹是以AB为直径的圆 时,点P的轨迹是以AB为直径的圆 |
您最近一年使用:0次
2022-08-08更新
|
1082次组卷
|
8卷引用:湖北省武汉市武钢三中2022-2023学年高二上学期10月月考数学试题
湖北省武汉市武钢三中2022-2023学年高二上学期10月月考数学试题湘教版(2019) 选修第一册 突围者 第3章 第一节 课时1 椭圆的标准方程2023版 北师大版(2019) 选修第一册 突围者 第二章 第一节 课时1 椭圆及其标准方程2023版 苏教版(2019) 选修第一册 突围者 第3章 第一节 课时1 椭圆的标准方程(已下线)3.1.1 椭圆的标准方程(3)3.1.1 椭圆的标准方程(同步练习基础版)(已下线)3.1.1椭圆及其标准方程 (分层作业)(3种题型分类基础练+能力提升练)-【上好课】高二数学同步备课系列(人教A版2019选择性必修第一册)(已下线)第3章 圆锥曲线的方程(基础、典型、易错、新文化、压轴)(1)
名校
解题方法
6 . 生活中,椭圆有很多光学性质,如从椭圆的一个焦点出发的光线射到椭圆镜面后反射,反射光线经过另一个焦点.现椭圆C的焦点在y轴上,中心在坐标原点,从下焦点 射出的光线经过椭圆镜面反射到上焦点
射出的光线经过椭圆镜面反射到上焦点 ,这束光线的总长度为4,且反射点与焦点构成的三角形面积最大值为
,这束光线的总长度为4,且反射点与焦点构成的三角形面积最大值为 ,已知椭圆的离心率e
,已知椭圆的离心率e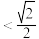 .
.
(1)求椭圆C的标准方程;
(2)若从椭圆C中心O出发的两束光线OM、ON,分别穿过椭圆上的A、B点后射到直线 上的M、N两点,若AB连线过椭圆的上焦点
上的M、N两点,若AB连线过椭圆的上焦点 ,试问,直线BM与直线AN能交于一定点吗?若能,求出此定点:若不能,请说明理由.
,试问,直线BM与直线AN能交于一定点吗?若能,求出此定点:若不能,请说明理由.
 射出的光线经过椭圆镜面反射到上焦点
射出的光线经过椭圆镜面反射到上焦点 ,这束光线的总长度为4,且反射点与焦点构成的三角形面积最大值为
,这束光线的总长度为4,且反射点与焦点构成的三角形面积最大值为 ,已知椭圆的离心率e
,已知椭圆的离心率e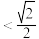 .
.(1)求椭圆C的标准方程;
(2)若从椭圆C中心O出发的两束光线OM、ON,分别穿过椭圆上的A、B点后射到直线
 上的M、N两点,若AB连线过椭圆的上焦点
上的M、N两点,若AB连线过椭圆的上焦点 ,试问,直线BM与直线AN能交于一定点吗?若能,求出此定点:若不能,请说明理由.
,试问,直线BM与直线AN能交于一定点吗?若能,求出此定点:若不能,请说明理由.
您最近一年使用:0次
2022-06-05更新
|
3796次组卷
|
11卷引用:湖北省部分高中联考协作体2023-2024学年高二上学期期中联考数学试题
湖北省部分高中联考协作体2023-2024学年高二上学期期中联考数学试题河南省焦作市博爱县第一中学2023-2024学年高二上学期9月月考数学试题河南省洛阳市第一高级中学2023-2024学年高二上学期期中达标数学测评卷(A卷)广东省汕头市潮阳实验学校2023-2024学年高二上学期期中数学试题(已下线)第3章 圆锥曲线的方程单元测试能力卷-2023-2024学年高二上学期数学人教A版(2019)选择性必修第一册(已下线)重组3 高二期中真题重组卷(广东卷)B提升卷安徽省合肥市第八中学2022届高三下学期高考最后一卷文科数学试题(已下线)专题24 圆锥曲线中的存在性、探索性问题 微点2 圆锥曲线中的探索性问题(已下线)专题25 圆锥曲线的光学性质及其应用 微点1 椭圆的光学性质及其应用(已下线)考向36 圆锥曲线中的定点、定值问题(重点)(已下线)专题43 圆锥曲线中的仿射变换、非对称韦达、光学性质问题-2
名校
解题方法
7 . 已知曲线 :
: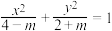 ,则( )
,则( )
 :
: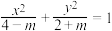 ,则( )
,则( )A. 时,则 时,则 的焦点是 的焦点是 , , |
B.当 时,则 时,则 的渐近线方程为 的渐近线方程为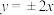 |
C.当 表示双曲线时,则 表示双曲线时,则 的取值范围为 的取值范围为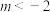 |
D.存在 ,使 ,使 表示圆 表示圆 |
您最近一年使用:0次
2021-12-10更新
|
1906次组卷
|
11卷引用:湖北省武汉市第十四中学2021-2022学年高二上学期12月月考数学试题
湖北省武汉市第十四中学2021-2022学年高二上学期12月月考数学试题黑龙江省哈尔滨工业大学附属中学校2021-2022学年高二上学期期末考试数学(理)试题重庆市第十一中学2021-2022学年高二下学期质量抽测(二)数学试题湖南省长沙市长郡中学2022-2023学年高二上学期期末数学试题第3章 双曲线与抛物线的方程及性质(培优卷)-【满分计划】2022-2023学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)(已下线)期末测试卷01(培优卷)-【满分计划】2022-2023学年高二数学阶段性复习测试卷(苏教版2019选择性必修第一册)江西省乐平中学2022-2023学年高二下学期3月月考数学试题江苏省扬州市邗江区邗江中学2023-2024学年高二上学期期中数学试题江苏省南京市中华中学2021-2022学年高三上学期期中数学试题(已下线)热点09 解析几何-2022年高考数学【热点·重点·难点】专练(新高考专用)(已下线)押全国卷(文科)第10,15题 平面解析几何-备战2022年高考数学(文)临考题号押题(全国卷)
名校
解题方法
8 . 如图所示,在平面直角坐标系中,椭圆 :
: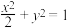 的左,右焦点外别为
的左,右焦点外别为 ,
, ,设P是第一象限内
,设P是第一象限内 上的一点,
上的一点,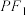 、
、 的延长线分别交
的延长线分别交 于点
于点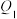 、
、 .
. 的周长;
的周长;
(2)求 面积的取值范围;
面积的取值范围;
(3)设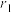 、
、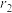 分别为
分别为 、
、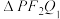 的内切圆半径,求
的内切圆半径,求 的最大值.
的最大值.
 :
: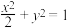 的左,右焦点外别为
的左,右焦点外别为 ,
, ,设P是第一象限内
,设P是第一象限内 上的一点,
上的一点,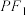 、
、 的延长线分别交
的延长线分别交 于点
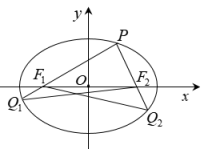
于点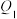 、
、 .
.
 的周长;
的周长;(2)求
 面积的取值范围;
面积的取值范围;(3)设
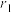 、
、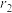 分别为
分别为 、
、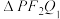 的内切圆半径,求
的内切圆半径,求 的最大值.
的最大值.
您最近一年使用:0次
2021-10-22更新
|
2286次组卷
|
10卷引用:湖北省黄石市有色第一中学2021-2022学年高二上学期期中数学试题
湖北省黄石市有色第一中学2021-2022学年高二上学期期中数学试题海南省海口中学2021-2022学年高二上学期期中考试数学试题上海市建平中学2022届高三上学期10月月考数学试题(已下线)第十一章 圆锥曲线专练13—椭圆大题(范围最值问题)-2022届高三数学一轮复习上海市嘉定区第一中学2023届高三三模数学试题上海市进才中学2024届高三上学期开学考试数学试题上海市育才中学2024届高三下学期第一次调研(3月)数学试题上海市嘉定区育才中学2024届高三下学期(3月份)一调数学试卷(已下线)信息必刷卷03(上海专用)湖南省长沙市第一中学2024届高三下学期高考适应性演练(二)数学试卷



