解题方法
1 . 已知等轴双曲线的顶点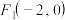 ,
,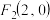 分别是椭圆
分别是椭圆 的左、右焦点,且
的左、右焦点,且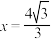 是椭圆与双曲线某个交点的横坐标.
是椭圆与双曲线某个交点的横坐标.
(1)求椭圆 的方程;
的方程;
(2)设直线 与椭圆
与椭圆 相交于
相交于 ,
, 两点,以线段
两点,以线段 为直径的圆过椭圆的上顶点
为直径的圆过椭圆的上顶点 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
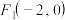 ,
,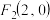 分别是椭圆
分别是椭圆 的左、右焦点,且
的左、右焦点,且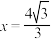 是椭圆与双曲线某个交点的横坐标.
是椭圆与双曲线某个交点的横坐标.(1)求椭圆
 的方程;
的方程;(2)设直线
 与椭圆
与椭圆 相交于
相交于 ,
, 两点,以线段
两点,以线段 为直径的圆过椭圆的上顶点
为直径的圆过椭圆的上顶点 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
您最近一年使用:0次
2021-04-15更新
|
1088次组卷
|
5卷引用:吉林省松原市长岭县第二中学2021届高三下学期三模考试数学试题
吉林省松原市长岭县第二中学2021届高三下学期三模考试数学试题2021届新高考同一套题信息原创卷(六)山东省(新高考)2021届数学学科仿真模拟标准卷试题(一)湖北省荆门市钟祥市实验中学2020-2021学年高二下学期4月阶段检测(3)数学试题(已下线)专题2.11 圆锥曲线-定点、定值、定直线问题-2021年高考数学解答题挑战满分专项训练(新高考地区专用)
名校
解题方法
2 . 椭圆 与
与 的中心在原点,焦点分别在
的中心在原点,焦点分别在 轴与
轴与 轴上,它们有相同的离心率
轴上,它们有相同的离心率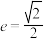 ,并且
,并且 的短轴为
的短轴为 的长轴,
的长轴, 与
与 的四个焦点构成的四边形面积是
的四个焦点构成的四边形面积是 .
.
(1)求椭圆 与
与 的方程;
的方程;
(2)设 是椭圆
是椭圆 上非顶点的动点,
上非顶点的动点, 与椭圆
与椭圆 长轴两个顶点
长轴两个顶点 ,
, 的连线
的连线 ,
, 分别与椭圆
分别与椭圆 交于
交于 ,
, 点.
点.
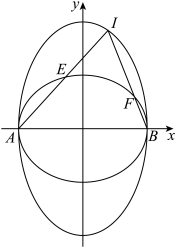
(i)求证:直线 ,
, 斜率之积为常数;
斜率之积为常数;
(ii)直线 与直线
与直线 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
 与
与 的中心在原点,焦点分别在
的中心在原点,焦点分别在 轴与
轴与 轴上,它们有相同的离心率
轴上,它们有相同的离心率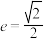 ,并且
,并且 的短轴为
的短轴为 的长轴,
的长轴, 与
与 的四个焦点构成的四边形面积是
的四个焦点构成的四边形面积是 .
.(1)求椭圆
 与
与 的方程;
的方程;(2)设
 是椭圆
是椭圆 上非顶点的动点,
上非顶点的动点, 与椭圆
与椭圆 长轴两个顶点
长轴两个顶点 ,
, 的连线
的连线 ,
, 分别与椭圆
分别与椭圆 交于
交于 ,
, 点.
点.(i)求证:直线
 ,
, 斜率之积为常数;
斜率之积为常数;(ii)直线
 与直线
与直线 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
您最近一年使用:0次
2017-08-17更新
|
231次组卷
|
6卷引用:吉林省松原市实验高级中学等三校2016届高三下学期联合模拟考试文数试题



