名校
解题方法
1 . 《文心雕龙》中说“造化赋形,支体必双,神理为用,事不孤立”,意思是自然界的事物都是成双成对的.已知动点 与定点
与定点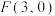 的距离和它到定直线
的距离和它到定直线 :
: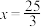 的距离的比是常数
的距离的比是常数 .若某条直线上存在这样的点
.若某条直线上存在这样的点 ,则称该直线为“成双直线”.则下列结论正确的是( )
,则称该直线为“成双直线”.则下列结论正确的是( )
 与定点
与定点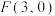 的距离和它到定直线
的距离和它到定直线 :
: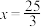 的距离的比是常数
的距离的比是常数 .若某条直线上存在这样的点
.若某条直线上存在这样的点 ,则称该直线为“成双直线”.则下列结论正确的是( )
,则称该直线为“成双直线”.则下列结论正确的是( )A.动点 的轨迹方程为 的轨迹方程为 |
B.动点 的轨迹与圆 的轨迹与圆 : :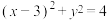 没有公共点 没有公共点 |
C.直线 : : 为成双直线 为成双直线 |
D.若直线 与点 与点 的轨迹相交于 的轨迹相交于 , , 两点,点 两点,点 为点 为点 的轨迹上不同于 的轨迹上不同于 , , 的一点,且直线 的一点,且直线 , , 的斜率分别为 的斜率分别为 , , ,则 ,则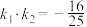 |
您最近一年使用:0次
2022-12-11更新
|
1189次组卷
|
9卷引用:吉林省长春市博硕学校(原北京师范大学长春附属学校)2022-2023学年高二上学期期中数学试题
吉林省长春市博硕学校(原北京师范大学长春附属学校)2022-2023学年高二上学期期中数学试题浙江省A9协作体2022-2023学年高二上学期期中联考数学试题四川省眉山中学校2022-2023学年高二上学期期中考试数学(理)试题四川省仁寿一中北校区2019-2020学年高二上学期期中考试理科数学试题广西玉林市北流市实验中学等四校2023-2024学年高二上学期期中联考质量评价检测数学试题山东省东营市2022-2023学年高二上学期期末考试数学试题黑龙江省哈尔滨师范大学附属中学2022-2023学年高二上学期期末考试数学试题(已下线)专题21 圆锥曲线中的轨迹方程的求法-2黑龙江省哈尔滨市第九中学校2023-2024学年高二上学期12月月考数学试题
名校
解题方法
2 . 阿基米德在他的著作《关于圆锥体和球体》中计算了一个椭圆的面积.当我们垂直地缩小一个圆时,我们得到一个椭圆,椭圆的面积等于圆周率 与椭圆的长半轴长与短半轴长的乘积,已知椭圆
与椭圆的长半轴长与短半轴长的乘积,已知椭圆 的面积为
的面积为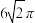 ,两个焦点分别为
,两个焦点分别为 ,点P为椭圆C的上顶点.直线
,点P为椭圆C的上顶点.直线 与椭圆C交于A,B两点,若
与椭圆C交于A,B两点,若 的斜率之积为
的斜率之积为 ,则椭圆C的长轴长为( )
,则椭圆C的长轴长为( )
 与椭圆的长半轴长与短半轴长的乘积,已知椭圆
与椭圆的长半轴长与短半轴长的乘积,已知椭圆 的面积为
的面积为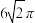 ,两个焦点分别为
,两个焦点分别为 ,点P为椭圆C的上顶点.直线
,点P为椭圆C的上顶点.直线 与椭圆C交于A,B两点,若
与椭圆C交于A,B两点,若 的斜率之积为
的斜率之积为 ,则椭圆C的长轴长为( )
,则椭圆C的长轴长为( )| A.3 | B.6 | C. | D. |
您最近一年使用:0次
2022-05-20更新
|
2127次组卷
|
8卷引用:吉林省延边市第二中学2023-2024学年高二上学期期中考试数学试卷
吉林省延边市第二中学2023-2024学年高二上学期期中考试数学试卷新疆维吾尔自治区伊犁哈萨克自治州霍尔果斯市苏港中学2022-2023学年高二下学期期中数学试题河北省唐山市2022届高三三模数学试题四川省内江市第六中学2021-2022学年高二下学期第2次月考数学(文科)试题 (已下线)专题5 阿基米德(已下线)重难点12五种椭圆解题方法-1四川省内江市高中2023届高三第三次模拟考试题数学(文科)试题(已下线)圆锥曲线新定义
名校
解题方法
3 . 阿基米德(公元前287年---公元前212年,古希腊)不仅是著名的哲学家、物理学家,也是著名的数学家,他利用“逼近法”得到椭圆面积除以圆周率 等于椭圆的长半轴长与短半轴长的乘积.在平面直角坐标系中,椭圆
等于椭圆的长半轴长与短半轴长的乘积.在平面直角坐标系中,椭圆 的面积等于
的面积等于 ,且椭圆
,且椭圆 的焦距为
的焦距为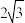 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)点 是
是 轴上的定点,直线
轴上的定点,直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,已知A关于
,已知A关于 轴的对称点为
轴的对称点为 ,
, 点关于原点的对称点为
点关于原点的对称点为 ,已知
,已知 三点共线,试探究直线
三点共线,试探究直线 是否过定点.若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点.若过定点,求出定点坐标;若不过定点,请说明理由.
 等于椭圆的长半轴长与短半轴长的乘积.在平面直角坐标系中,椭圆
等于椭圆的长半轴长与短半轴长的乘积.在平面直角坐标系中,椭圆 的面积等于
的面积等于 ,且椭圆
,且椭圆 的焦距为
的焦距为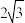 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)点
 是
是 轴上的定点,直线
轴上的定点,直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,已知A关于
,已知A关于 轴的对称点为
轴的对称点为 ,
, 点关于原点的对称点为
点关于原点的对称点为 ,已知
,已知 三点共线,试探究直线
三点共线,试探究直线 是否过定点.若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点.若过定点,求出定点坐标;若不过定点,请说明理由.
您最近一年使用:0次
2021-10-08更新
|
1499次组卷
|
10卷引用:吉林省通化市梅河口市第五中学2021-2022学年高二上学期期中数学试题
吉林省通化市梅河口市第五中学2021-2022学年高二上学期期中数学试题广东省广州市广州大学附属中学、铁一中学、广州外国语学校2021-2022学年高二上学期期中三校联考数学试题宁夏银川市景博中学2022届高三上学期期中考试数学(文)试题广东省深圳市富源学校2023-2024学年高二上学期期中数学试题重庆市育才中学2022届高三上学期高考适应性考试(三)数学试题(已下线)数学与数学家(已下线)9.6 三定问题及最值(精讲)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)福建省莆田第二十五中学2021-2022学年高二上学期期末考试数学试题(已下线)卷13 高二上学期第二次阶段测试卷01 -【重难点突破】2021-2022学年高二数学名校好题汇编同步测试卷(人教A版选择性必修第二册)浙江省杭州第四中学吴山校区2022-2023学年高二上学期期末数学试题



