名校
解题方法
1 . 已知抛物线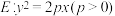 的焦点为F,点P在抛物线E上,点P的横坐标为1,且
的焦点为F,点P在抛物线E上,点P的横坐标为1,且 是抛物线E上异于O的两点.
是抛物线E上异于O的两点.
(1)求抛物线E的标准方程;
(2)若直线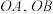 的斜率之积为
的斜率之积为 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
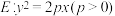 的焦点为F,点P在抛物线E上,点P的横坐标为1,且
的焦点为F,点P在抛物线E上,点P的横坐标为1,且 是抛物线E上异于O的两点.
是抛物线E上异于O的两点.(1)求抛物线E的标准方程;
(2)若直线
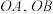 的斜率之积为
的斜率之积为 ,求证:直线
,求证:直线 恒过定点.
恒过定点.
您最近一年使用:0次
2023-02-14更新
|
823次组卷
|
2卷引用:宁夏吴忠市青铜峡市宁朔中学2023-2024学年高二上学期期末数学试卷
名校
解题方法
2 . 在平面直角坐标系 中,已知抛物线
中,已知抛物线 上一点
上一点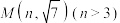 到其焦点
到其焦点 的距离为
的距离为 .
.
(1)求抛物线的方程与准线方程;
(2)直线 与抛物线相交于
与抛物线相交于 两点(
两点( 位于
位于 轴的两侧),若
轴的两侧),若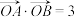 ,求证直线
,求证直线 恒过定点.
恒过定点.
 中,已知抛物线
中,已知抛物线 上一点
上一点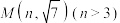 到其焦点
到其焦点 的距离为
的距离为 .
.(1)求抛物线的方程与准线方程;
(2)直线
 与抛物线相交于
与抛物线相交于 两点(
两点( 位于
位于 轴的两侧),若
轴的两侧),若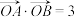 ,求证直线
,求证直线 恒过定点.
恒过定点.
您最近一年使用:0次
2020-02-27更新
|
414次组卷
|
3卷引用:宁夏青铜峡市宁朔中学2023-2024学年高二上学期第二次月考数学试题
3 . 已知抛物线的顶点在原点,准线方程为 ,
, 是焦点,过点
是焦点,过点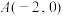 的直线与抛物线交于
的直线与抛物线交于 两点,直线
两点,直线 分别交抛物线于点
分别交抛物线于点 .
.
(1)求抛物线的方程及 的值;
的值;
(2)记直线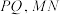 的斜率分别为
的斜率分别为 ,证明:
,证明: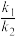 为定值.
为定值.
 ,
, 是焦点,过点
是焦点,过点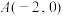 的直线与抛物线交于
的直线与抛物线交于 两点,直线
两点,直线 分别交抛物线于点
分别交抛物线于点 .
.(1)求抛物线的方程及
 的值;
的值;(2)记直线
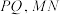 的斜率分别为
的斜率分别为 ,证明:
,证明: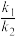 为定值.
为定值.
您最近一年使用:0次
2016-12-04更新
|
446次组卷
|
2卷引用:2016届宁夏六盘山高中高三第三次模拟考试文科数学试卷



