1 . 魔方,又叫鲁比可方块,最早是由匈牙利布达佩斯建筑学院厄尔诺·鲁比克教授于1974年发明的机械益智玩具.魔方拥有竞速、盲拧、单拧等多种玩法,风靡程度经久未衰,每年都会举办大小赛事,是最受欢迎的智力游戏之一.通常意义下的魔方,是指狭义的三阶魔方.三阶魔方形状通常是正方体,由有弹性的硬塑料制成.常规竞速玩法是将魔方打乱,然后在最短的时间内复原.广义的魔方,指各类可以通过转动打乱和复原的几何体.魔方与华容道、法国的单身贵族(独立钻石棋)并称为智力游戏界的三大不可思议.在2018WCA世界魔方芜湖公开赛上,杜宇生以3.47秒的成绩打破了三阶魔方复原的世界纪录,勇夺世界魔方运动的冠军,并成为世界上第一个三阶魔方速拧进入4秒的选手.
(1)小王和小吴同学比赛三阶魔方,已知小王每局比赛获胜的概率均为 ,小吴每局比赛获胜的概率均为
,小吴每局比赛获胜的概率均为 ,若采用三局两胜制,两人共进行了
,若采用三局两胜制,两人共进行了 局比赛,求
局比赛,求 的分布列和数学期望;
的分布列和数学期望;
(2)小王和小吴同学比赛四阶魔方,首局比赛小吴获胜的概率为0.5,若小王本局胜利,则他赢得下一局比赛的概率为0.6,若小王本局失败,则他赢得下一局比赛的概率为0.5,为了赢得比赛,小王应选择“五局三胜制”还是“三局两胜制”?
(1)小王和小吴同学比赛三阶魔方,已知小王每局比赛获胜的概率均为
 ,小吴每局比赛获胜的概率均为
,小吴每局比赛获胜的概率均为 ,若采用三局两胜制,两人共进行了
,若采用三局两胜制,两人共进行了 局比赛,求
局比赛,求 的分布列和数学期望;
的分布列和数学期望;(2)小王和小吴同学比赛四阶魔方,首局比赛小吴获胜的概率为0.5,若小王本局胜利,则他赢得下一局比赛的概率为0.6,若小王本局失败,则他赢得下一局比赛的概率为0.5,为了赢得比赛,小王应选择“五局三胜制”还是“三局两胜制”?
您最近一年使用:0次
2023-12-18更新
|
1136次组卷
|
5卷引用:7.3.1 离散型随机变量的均值——课后作业(巩固版)
(已下线)7.3.1 离散型随机变量的均值——课后作业(巩固版)山西省临汾市同盛实验中学2024届高三核心模拟(中)数学试题(四)江西省新余市2023-2024学年高三上学期期末质量检测数学试卷(已下线)第04讲 7.3.1离散型随机变量的均值-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)专题7.10 随机变量及其分布全章综合测试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
解题方法
2 . 第19届亚运会将于2023年9月23日至10月8日举办,本届亚运会共设40个竞赛大项.其中首次增设了电子竞技项目.与传统的淘汰赛不同,近年来一个新型的赛制“双败赛制”赢得了许多赛事的青睐.传统的淘汰赛失败一场就丧失了冠军争夺的权利,而在双败赛制下,每人或者每个队伍只有失败了两场才会淘汰出局,因此更有容错率.假设最终进入到半决赛有四支队伍,淘汰赛制下会将他们四支队伍两两分组进行比赛,胜者进入到总决赛,总决赛的胜者即为最终的冠军.双败赛制下,两两分组,胜者进入到胜者组,败者进入到败者组,胜者组两个队伍对决的胜者将进入到总决赛,败者进入到败者组.之前进入到败者组的两个队伍对决的败者将直接淘汰,胜者将跟胜者组的败者对决,其中的胜者进入总决赛,最后总决赛的胜者即为冠军,双败赛制下会发现一个有意思的事情,在胜者组中的胜者只要输一场比赛即总决赛就无法拿到冠军,但是其它的队伍却有一次失败的机会,近年来从败者组杀上来拿到冠军的不在少数,因此很多人戏谑这个赛制对强者不公平,是否真的如此呢?

这里我们简单研究一下两个赛制,假设四支队伍分别为A、B、C、D,其中A对阵其他三个队伍获胜概率均为p,另外三支队伍彼此之间对阵时获胜概率均为 .最初分组时AB同组,CD同组.
.最初分组时AB同组,CD同组.
(1)若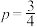 ,在淘汰赛赛制下,A、C获得冠军的概率分别为多少?
,在淘汰赛赛制下,A、C获得冠军的概率分别为多少?
(2)分别计算两种赛制下A获得冠军的概率(用 表示),并据此简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?
表示),并据此简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?

这里我们简单研究一下两个赛制,假设四支队伍分别为A、B、C、D,其中A对阵其他三个队伍获胜概率均为p,另外三支队伍彼此之间对阵时获胜概率均为
 .最初分组时AB同组,CD同组.
.最初分组时AB同组,CD同组.(1)若
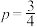 ,在淘汰赛赛制下,A、C获得冠军的概率分别为多少?
,在淘汰赛赛制下,A、C获得冠军的概率分别为多少?(2)分别计算两种赛制下A获得冠军的概率(用
 表示),并据此简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?
表示),并据此简单分析一下双败赛制下对队伍的影响,是否如很多人质疑的“对强者不公平”?
您最近一年使用:0次
2023-10-10更新
|
1118次组卷
|
9卷引用:12.4 随机事件的独立性(四大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)
(已下线)12.4 随机事件的独立性(四大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)湖北省黄冈市黄州中学(黄冈外校)2023-2024学年高二实验朝阳班上学期9月阶段性测试数学试题安徽省合肥市长丰县第一中学2023-2024学年高二上学期第一次月考数学考试试题(已下线)专题03 条件概率与全概率公式(2)(已下线)专题10.6 概率全章八大压轴题型归纳(拔尖篇-举一反三系列(人教A版2019必修第二册)单元测试B卷——第十章?概率(已下线)专题25 互斥事件和独立事件-《重难点题型·高分突破》(苏教版2019必修第二册)(已下线)高一下学期期末复习解答题压轴题二十四大题型专练(2)-举一反三系列(人教A版2019必修第二册)(已下线)专题10.8 概率全章综合测试卷(提高篇)-举一反三系列(人教A版2019必修第二册)
名校
解题方法
3 . 如图,甲乙做游戏,两人通过划拳(剪刀、石头、布)比赛决胜谁首先登上第3个台阶,并规定从平地开始,每次划拳赢的一方登上一级台阶,输的一方原地不动,平局时两人都上一个台阶.如果一方连续赢两次,那么他将额外获得上一级台阶的奖励,除非已经登上第3个台阶,当有任何一方登上第3个台阶时游戏结束,则游戏结束时恰好划拳3次的概率为______ .

您最近一年使用:0次
2023-09-24更新
|
1095次组卷
|
7卷引用:12.4 随机事件的独立性(四大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)
(已下线)12.4 随机事件的独立性(四大题型)(分层练习)-2023-2024学年高二数学同步精品课堂(沪教版2020必修第三册)(已下线)4.1.2 乘法公式与全概率公式(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)吉林省东北师范大学附属中学2023-2024学年高二上学期第一次月考数学试题(已下线)第12章 概率初步(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(沪教版2020必修第三册)浙江省绍兴市第一中学2023-2024学年高一下学期创新班期中考试数学试卷(已下线)高一下学期期末复习填空题压轴题二十三大题型专练(2)-举一反三系列(人教A版2019必修第二册)(已下线)第06讲 第十章 概率 章末题型大总结-【帮课堂】(人教A版2019必修第二册)
4 . 已知共15张卡牌由5张红卡、10张其它颜色卡组成,混合后分3轮发出,每轮随机发出5张卡.
(1)求事件“第1轮无红色卡牌”的概率 ;
;
(2)求事件“第1轮有至少3张红色卡牌”的概率 ;
;
(3)求事件“每轮均有红色卡牌”的概率 .
.
(1)求事件“第1轮无红色卡牌”的概率
 ;
;(2)求事件“第1轮有至少3张红色卡牌”的概率
 ;
;(3)求事件“每轮均有红色卡牌”的概率
 .
.
您最近一年使用:0次
2022-11-05更新
|
1173次组卷
|
7卷引用:7.4.2 超几何分布 (精练)-【精讲精练】2022-2023学年高二数学下学期同步精讲精练(人教A版2019选择性必修第三册)
(已下线)7.4.2 超几何分布 (精练)-【精讲精练】2022-2023学年高二数学下学期同步精讲精练(人教A版2019选择性必修第三册)(已下线)4.2.3二项分布与超几何分布(2)上海市嘉定区安亭高级中学2022-2023学年高二上学期期中数学试题(已下线)第七章 随机变量及其分布(A卷·知识通关练)(3)(已下线)第四章 概率与统计(A卷·知识通关练)(2)(已下线)7.4.2超几何分布(分层作业)-【上好课】2022-2023学年高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)高二下期中真题精选(压轴40题专练)-【满分全攻略】2022-2023学年高二数学下学期核心考点+重难点讲练与测试(沪教版2020选修一+选修二)
名校
5 . 甲,乙两人进行围棋比赛,采取积分制,规则如下:每胜1局得1分,负1局或平局都不得分,积分先达到2分者获胜;若第四局结束,没有人积分达到2分,则积分多的一方获胜;若第四局结束,没有人积分达到2分,且积分相等,则比赛最终打平.假设在每局比赛中,甲胜的概率为 ,负的概率为
,负的概率为 ,且每局比赛之间的胜负相互独立.
,且每局比赛之间的胜负相互独立.
(1)求第三局结束时乙获胜的概率;
(2)求甲获胜的概率.
 ,负的概率为
,负的概率为 ,且每局比赛之间的胜负相互独立.
,且每局比赛之间的胜负相互独立.(1)求第三局结束时乙获胜的概率;
(2)求甲获胜的概率.
您最近一年使用:0次
2022-07-07更新
|
4438次组卷
|
18卷引用:专题10.4 事件的相互独立性(重难点题型检测)-2022-2023学年高一数学举一反三系列(人教A版2019必修第二册)
(已下线)专题10.4 事件的相互独立性(重难点题型检测)-2022-2023学年高一数学举一反三系列(人教A版2019必修第二册)河北省邢台市2021-2022学年高一下学期期末数学试题河北省承德市2021-2022学年高一下学期期末数学试题湖南省衡阳市祁东县2021-2022学年高一下学期期末数学试题河南省安阳市第一中学2022-2023学年高一下学期5月月考数学试题(已下线)模块三 专题8 (统计与概率)(拔高能力练)(人教A版)(已下线)模块三 专题9 大题分类连(统计与概率)(拔高能力练)(苏教版)河北省石家庄市辛集市2022-2023学年高一下学期期末数学试题福建省宁德第一中学2022-2023学年高一下学期期末质量检测数学试题湖南省湘潭市湘乡市名民实验学校2023-2024学年高二上学期入学考试数学试题湖北省宜昌市部分省级示范高中2023-2024学年高二上学期11月月考数学试卷(已下线)第七章 概率章末测试--同步精品课堂(北师大版2019必修第一册)广东省韶关市广东北江实验学校2023-2024学年高二上学期第二次月考(12月)数学试题河北省石家庄市2023-2024学年高二上学期期末教学质量检测数学试题(已下线)概 率专题14概率(已下线)高一下学期期末复习解答题压轴题二十四大题型专练(2)-举一反三系列(人教A版2019必修第二册)(已下线)第06讲 第十章 概率 章末题型大总结-【帮课堂】(人教A版2019必修第二册)
名校
解题方法
6 . 某学校组织校园安全知识竞赛.在初赛中有两轮答题,第一轮从A类的5个问题中任选两题作答,若两题都答对,则得40分,否则得0分;第二轮从B类的5个问题中任选两题作答,每答对1题得30分,答错得0分若两轮总积分不低于60分则晋级复赛.
小芳和小明同时参赛,已知小芳每个问题答对的概率都为0.5.在A类的5个问题中,小明只能答对4个问题;在B类的5个问题中,小明每个问题答对的概率都为0.4.他们回答任一问题正确与否互不影响.
(1)求小明在第一轮得40分的概率;
(2)以晋级复赛的概率大小为依据,小芳和小明谁更容易晋级复赛?
小芳和小明同时参赛,已知小芳每个问题答对的概率都为0.5.在A类的5个问题中,小明只能答对4个问题;在B类的5个问题中,小明每个问题答对的概率都为0.4.他们回答任一问题正确与否互不影响.
(1)求小明在第一轮得40分的概率;
(2)以晋级复赛的概率大小为依据,小芳和小明谁更容易晋级复赛?
您最近一年使用:0次
2022-07-05更新
|
3647次组卷
|
22卷引用:4.1.3独立性与条件概率的关系(2)
(已下线)4.1.3独立性与条件概率的关系(2)福建省厦门市2021-2022学年高一下学期质量检测(期末)数学试题山东省威海市乳山市银滩高级中学2022-2023学年高二下学期4月月考数学试题(已下线)10.2 事件的相互独立性(精练)-2022-2023学年高一数学一隅三反系列(人教A版2019必修第二册)(已下线)专题强化 事件、古典概率各类问题一遍过-《考点·题型·技巧》(已下线)高一下学期期末考点大通关真题精选100题(3)-期中期末考点大串讲(已下线)模块三 专题8 (统计与概率)(拔高能力练)(人教A版)(已下线)模块三 专题9 大题分类连(统计与概率)(拔高能力练)(苏教版)河南省信阳市信阳高级中学2022-2023学年高一下学期期末数学试题甘肃省天水市第一中学2023-2024学年高二上学期开学考试数学试题黑龙江省大庆市大庆实验中学2023-2024学年高二上学期10月月考数学试题广东省博罗县2023-2024学年高二上学期期中数学试题广东省惠州市大亚湾区第一中学2023-2024学年高二上学期期中检测数学试卷(已下线)第12章 概率初步(压轴题专练)-2023-2024学年高二数学单元速记·巧练(沪教版2020必修第三册)专题14概率(已下线)第十章 概率(压轴题专练)-单元速记·巧练(人教A版2019必修第二册)(已下线)第15章 概率单元综合能力测试卷-【帮课堂】(苏教版2019必修第二册)(已下线)专题10.2 事件的相互独立性-举一反三系列(人教A版2019必修第二册)(已下线)第15章 概率章末题型归纳总结-【帮课堂】(苏教版2019必修第二册)(已下线)专题02 事件的相互独立性(题型专练)-《知识解读·题型专练》(人教A版2019必修第二册)(已下线)高一下学期期末数学试卷(提高篇)-举一反三系列(人教A版2019必修第二册)(已下线)高一下学期期末复习解答题压轴题二十四大题型专练(2)-举一反三系列(人教A版2019必修第二册)
名校
解题方法
7 . 甲罐中有5个红球,2个白球和3个黑球, 乙罐中有4个红球,3个白球和3个黑球(球除颜色外,大小质地均相同).先从甲罐中随机取出一球放入乙罐,分别以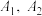 和
和 表示由甲罐中取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B表示由乙罐中取出的球是红球的事件.下列结论正确的个数是( )
表示由甲罐中取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B表示由乙罐中取出的球是红球的事件.下列结论正确的个数是( )
①事件 与
与 相互独立;
相互独立;
② ,
, ,
, 是两两互斥的事件;
是两两互斥的事件;
③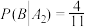 ;
;
④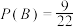 ;
;
⑤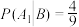
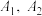 和
和 表示由甲罐中取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B表示由乙罐中取出的球是红球的事件.下列结论正确的个数是( )
表示由甲罐中取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以B表示由乙罐中取出的球是红球的事件.下列结论正确的个数是( )①事件
 与
与 相互独立;
相互独立;②
 ,
, ,
, 是两两互斥的事件;
是两两互斥的事件; ③
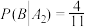 ;
;④
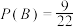 ;
;⑤
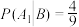
| A.5 | B.4 | C.3 | D.2 |
您最近一年使用:0次
2022-03-25更新
|
5543次组卷
|
11卷引用:4.1.3独立性与条件概率的关系(1)
(已下线)4.1.3独立性与条件概率的关系(1)山西省长治市第二中学校2021-2022学年高二下学期第一次月考数学试题(已下线)专题11 条件概率公式、全概率公式、贝叶斯公式、乘法公式-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)(已下线)7.1.2 全概率公式(分层作业)-【上好课】2022-2023学年高二数学同步备课系列(人教A版2019选择性必修第三册)黑龙江省哈尔滨市哈工大附中2024届高三上学期期中数学试题陕西省西安市2024年高三第一次质量检测理科数学试题(已下线)概 率(已下线)大招1 条件概率与全概率公式&贝叶斯公式专题14条件概率与全概率公式(已下线)专题05 统计与概率-【常考压轴题】(已下线)高二下学期期中复习选择题压轴题十五大题型专练-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
名校
解题方法
8 . 一个不透明的口袋中有8个大小相同的球,其中红球5个,白球1个,黑球2个,则下列选项正确的有( )
A.从该口袋中任取3个球,设取出的红球个数为 ,则数学期望 ,则数学期望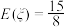 |
B.每次从该口袋中任取一个球,记录下颜色后放回口袋,先后取了3次,设取出的黑球次数为 ,则数学期望 ,则数学期望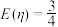 |
C.从该口袋中任取3个球,设取出的球的颜色有X种,则数学期望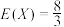 |
D.每次从该口袋中任取一个球,不放回,拿出红球即停,设拿出的黑球的个数为Y,则数学期望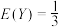 |
您最近一年使用:0次
2022-02-28更新
|
2959次组卷
|
7卷引用:3.2.3 离散型随机变量的数学期望(同步练习)-【素养提升—课时练】2022-2023学年高二数学湘教版选择性必修第二册检测 (基础篇)
(已下线)3.2.3 离散型随机变量的数学期望(同步练习)-【素养提升—课时练】2022-2023学年高二数学湘教版选择性必修第二册检测 (基础篇)辽宁省大连市瓦房店市高级中学2021-2022学年高二上学期期末数学试题山东省学情联考2021-2022学年高二下学期3月阶段性质量检测数学试题(A)(已下线)第07讲 二项分布与超几何分布及正态分布(核心考点讲与练)(2)辽宁省重点高中协作校2021-2022学年高二上学期期末数学试题(已下线)第八章 概率(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)重庆市南开中学校2023-2024学年高二下学期阶段测试数学试题
名校
解题方法
9 . 某新型双轴承电动机需要装配两个轴承才能正常工作,且两个轴承互不影响.现计划购置甲,乙两个品牌的轴承,两个品牌轴承的使用寿命及价格情况如下表:
已知甲品牌使用 个月或
个月或 个月的概率均为
个月的概率均为 ,乙品牌使用
,乙品牌使用 个月或
个月或 个月的概率均为
个月的概率均为 .
.
(1)若从 件甲品牌和
件甲品牌和 件乙品牌共
件乙品牌共 件轴承中,任选
件轴承中,任选 件装入电动机内,求电动机可工作时间不少于
件装入电动机内,求电动机可工作时间不少于 个月的概率;
个月的概率;
(2)现有两种购置方案,方案一:购置 件甲品牌;方案二:购置
件甲品牌;方案二:购置 件甲品牌和
件甲品牌和 件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
品牌 | 价格(元/件) | 使用寿命(月) |
甲 |
|
|
乙 |
|
|
 个月或
个月或 个月的概率均为
个月的概率均为 ,乙品牌使用
,乙品牌使用 个月或
个月或 个月的概率均为
个月的概率均为 .
.(1)若从
 件甲品牌和
件甲品牌和 件乙品牌共
件乙品牌共 件轴承中,任选
件轴承中,任选 件装入电动机内,求电动机可工作时间不少于
件装入电动机内,求电动机可工作时间不少于 个月的概率;
个月的概率;(2)现有两种购置方案,方案一:购置
 件甲品牌;方案二:购置
件甲品牌;方案二:购置 件甲品牌和
件甲品牌和 件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
您最近一年使用:0次
2021-04-29更新
|
2670次组卷
|
6卷引用:人教A版(2019) 选修第三册 过关斩将 第七章 7.3.1 离散型随机变量的均值
人教A版(2019) 选修第三册 过关斩将 第七章 7.3.1 离散型随机变量的均值山东省泰安市2021届高三二模数学试题湖南省长沙市雅礼中学2021-2022学年高三上学期入学考试数学试题(已下线)第51讲 概率与统计综合问题-2022年新高考数学二轮专题突破精练山西省运城市芮城中学2021-2022学年高二下学期第一次月考数学试题(已下线)专题13 概率综合问题-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)
2021·全国·模拟预测
名校
10 . 受新冠肺炎疫情的影响,2020年一些企业改变了针对应届毕业生的校园招聘方式,将线下招聘改为线上招聘.某世界五百强企业 的线上招聘方式分资料初审、笔试、面试这三个环节进行,资料初审通过后才能进行笔试,笔试合格后才能参加面试,面试合格后便正式录取,且这几个环节能否通过相互独立.现有甲、乙、丙三名大学生报名参加了企业
的线上招聘方式分资料初审、笔试、面试这三个环节进行,资料初审通过后才能进行笔试,笔试合格后才能参加面试,面试合格后便正式录取,且这几个环节能否通过相互独立.现有甲、乙、丙三名大学生报名参加了企业 的线上招聘,并均已通过了资料初审环节.假设甲通过笔试、面试的概率分别为
的线上招聘,并均已通过了资料初审环节.假设甲通过笔试、面试的概率分别为  ,
, ;乙通过笔试、面试的概率分别为
;乙通过笔试、面试的概率分别为 ,
, ;丙通过笔试、面试的概率与乙相同.
;丙通过笔试、面试的概率与乙相同.
(1)求甲、乙、丙三人中恰有一人被企业 正式录取的概率;
正式录取的概率;
(2)求甲、乙、丙三人中至少有一人被企业 正式录取的概率;
正式录取的概率;
(3)为鼓励优秀大学生积极参与企业的招聘工作,企业 决定给报名参加应聘且通过资料初审的大学生一定的补贴,补贴标准如下表:
决定给报名参加应聘且通过资料初审的大学生一定的补贴,补贴标准如下表:
记甲、乙、丙三人获得的所有补贴之和为 元,求
元,求 的分布列和数学期望.
的分布列和数学期望.
 的线上招聘方式分资料初审、笔试、面试这三个环节进行,资料初审通过后才能进行笔试,笔试合格后才能参加面试,面试合格后便正式录取,且这几个环节能否通过相互独立.现有甲、乙、丙三名大学生报名参加了企业
的线上招聘方式分资料初审、笔试、面试这三个环节进行,资料初审通过后才能进行笔试,笔试合格后才能参加面试,面试合格后便正式录取,且这几个环节能否通过相互独立.现有甲、乙、丙三名大学生报名参加了企业 的线上招聘,并均已通过了资料初审环节.假设甲通过笔试、面试的概率分别为
的线上招聘,并均已通过了资料初审环节.假设甲通过笔试、面试的概率分别为  ,
, ;乙通过笔试、面试的概率分别为
;乙通过笔试、面试的概率分别为 ,
, ;丙通过笔试、面试的概率与乙相同.
;丙通过笔试、面试的概率与乙相同.(1)求甲、乙、丙三人中恰有一人被企业
 正式录取的概率;
正式录取的概率;(2)求甲、乙、丙三人中至少有一人被企业
 正式录取的概率;
正式录取的概率;(3)为鼓励优秀大学生积极参与企业的招聘工作,企业
 决定给报名参加应聘且通过资料初审的大学生一定的补贴,补贴标准如下表:
决定给报名参加应聘且通过资料初审的大学生一定的补贴,补贴标准如下表:| 参与环节 | 笔试 | 面试 |
| 补贴(元) | 100 | 200 |
 元,求
元,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
2021-03-03更新
|
4834次组卷
|
11卷引用:专题7.3离散型随机变量的数字特征(B卷提升篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)
(已下线)专题7.3离散型随机变量的数字特征(B卷提升篇)-2020-2021学年高二下学期数学选择性必修第三册同步单元AB卷(新教材人教A版,浙江专用)(已下线)2021新高考普通高等学校招生全国统一考试数学考向卷(一)(已下线)专题34 随机变量及其分布(解答题)-2021年高考数学(理)二轮复习热点题型精选精练(已下线)专题32 随机变量及其分布(解答题)-2021年高考数学二轮复习热点题型精选精练(新高考地区专用)(已下线)专题11 随机变量及其应用-备战2021年高考数学二轮复习题型专练(新高考专用)福建省三明第一中学2021届高三5月校模拟考数学试题江苏省扬州中学2020-2021学年高二下学期5月月考数学试题(已下线)第七章 随机变量及其分布单元测试(提升卷)-2020-2021学年高二数学新教材单元双测卷(人教A版2019选择性必修第三册)福建省上杭一中、永定一中2022届高三上学期第一次联考数学试题(已下线)8.2.2 离散型随机变量的数字特征(练习)-2022-2023学年高二数学同步精品课堂(苏教版2019选择性必修第二册)(已下线)第7章 随机变量及其分布 单元综合检测-2022-2023学年高二数学同步精品课堂(人教A版2019选择性必修第三册)





