名校
解题方法
1 . 一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯(卫生习惯分为良好和不够良好两类)的关系,在已患该疾病的病例中随机调查了100例(称为病例组),同时在未患该疾病的人群中随机调查了100人(称为对照组),得到如下数据:
从该地的人群中任选一人, 表示事件“选到的人卫生习惯不够良好”,
表示事件“选到的人卫生习惯不够良好”,  表示事件“选到的人患有该疾病”,
表示事件“选到的人患有该疾病”,  与
与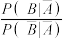 的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为
的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为 .
.
(1)证明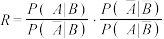 ;
;
(2)利用该调查数据,给出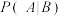 ,
,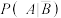 的估计值,并利用(1)的结果给出
的估计值,并利用(1)的结果给出 的估计值.
的估计值.
不够良好 | 良好 | |
病例组 | 40 | 60 |
对照组 | 10 | 90 |
 表示事件“选到的人卫生习惯不够良好”,
表示事件“选到的人卫生习惯不够良好”,  表示事件“选到的人患有该疾病”,
表示事件“选到的人患有该疾病”,  与
与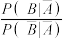 的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为
的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标,记该指标为 .
.(1)证明
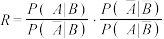 ;
;(2)利用该调查数据,给出
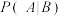 ,
,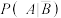 的估计值,并利用(1)的结果给出
的估计值,并利用(1)的结果给出 的估计值.
的估计值.
您最近一年使用:0次
2024-04-01更新
|
594次组卷
|
6卷引用:广东省佛山市南海区九江中学2021-2022学年高二下学期6月校内三检数学试题
广东省佛山市南海区九江中学2021-2022学年高二下学期6月校内三检数学试题河南省灵宝市第一高级中学2022-2023学年高二下学期月清考试数学试题(已下线)第06讲 条件概率和全概率公式及应用3种常考题型(已下线)7.1.1条件概率7.1.2全概率公式 第三课 知识扩展延伸(已下线)专题04 条件概率与全概率公式(6类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)(已下线)专题7 第1讲 概率、随机变量及其分布列
名校
2 . 在信道内传输0, 1信号,信号的传输相互独立.发送0时,收到1的概率为 ,收到0的概率为
,收到0的概率为 ;发送1时,收到0的概率为
;发送1时,收到0的概率为 , 收到1的概率为
, 收到1的概率为 .
.
(1)重复发送信号1三次,计算至少收到两次1的概率;
(2)依次发送1,1, 0, 判断以下两个事件:①事件A:至少收到一个正确信号; ②事件B:至少收到两个0,是否互相独立,并给出证明.
 ,收到0的概率为
,收到0的概率为 ;发送1时,收到0的概率为
;发送1时,收到0的概率为 , 收到1的概率为
, 收到1的概率为 .
.(1)重复发送信号1三次,计算至少收到两次1的概率;
(2)依次发送1,1, 0, 判断以下两个事件:①事件A:至少收到一个正确信号; ②事件B:至少收到两个0,是否互相独立,并给出证明.
您最近一年使用:0次
2023-11-07更新
|
2417次组卷
|
19卷引用:广东省佛山市石门中学2024-2025学年高二上学期第一次月考数学试题
广东省佛山市石门中学2024-2025学年高二上学期第一次月考数学试题广东省佛山市顺德区乐从中学2024-2025学年高二上学期第一次质量检测数学试题浙江省杭州第二中学2023-2024学年高二上学期期中数学试题上海市上海中学2023-2024学年高二上学期期末考试数学试题(已下线)专题07概率初步(续)--高二期末考点大串讲(沪教版2020选修)(已下线)专题20 随机事件的独立性- 【暑假自学课】(沪教版2020)四川省高县中学校2023-2024学年高二上学期期中考试数学试卷(已下线)专题05 统计与概率-【常考压轴题】(已下线)第十章 概率(压轴题专练)-单元速记·巧练(人教A版2019必修第二册)(已下线)专题10.2 事件的相互独立性-举一反三系列(人教A版2019必修第二册)河北省沧州市泊头市第一中学2023-2024学年高一下学期5月月考数学试题(已下线)第06讲 第十章 概率 章末题型大总结-【帮课堂】(人教A版2019必修第二册)(已下线)第04讲 10.2 事件的相互独立性-【帮课堂】(人教A版2019必修第二册)(已下线)10.2事件的相互独立性【第二练】“上好三节课,做好三套题“高中数学素养晋级之路(已下线)10.2 事件的相互独立性-同步题型分类归纳讲与练(人教A版2019必修第二册)(已下线)专题3 以复杂事件为背景的概率求解问题【练】(高一期末压轴专项)(已下线)模型2 事件相互独立的应用(第10章 概率)(已下线)专题1 概率压轴大题(过关集训)(已下线)第二章 概率 专题三 独立事件 微点2 独立事件综合训练【基础版】
3 . 设集合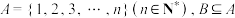 ,且
,且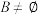 ,记集合
,记集合 中的最小元素和最大元素分别为随机变量
中的最小元素和最大元素分别为随机变量 .
.
(1)若 的概率为
的概率为 ,求
,求 ;
;
(2)若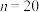 ,求
,求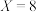 且
且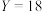 的概率;
的概率;
(3)记随机变量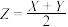 ,证明:
,证明: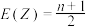 .
.
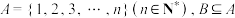 ,且
,且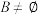 ,记集合
,记集合 中的最小元素和最大元素分别为随机变量
中的最小元素和最大元素分别为随机变量 .
.(1)若
 的概率为
的概率为 ,求
,求 ;
;(2)若
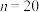 ,求
,求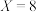 且
且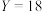 的概率;
的概率;(3)记随机变量
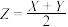 ,证明:
,证明: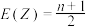 .
.
您最近一年使用:0次
名校
4 . 由 个小正方形构成长方形网格有
个小正方形构成长方形网格有 行和
行和 列.每次将一个小球放到一个小正方形内,放满为止,记为一轮.每次放白球的频率为
列.每次将一个小球放到一个小正方形内,放满为止,记为一轮.每次放白球的频率为 ,放红球的概率为q,
,放红球的概率为q, .
.
(1)若 ,
, ,记
,记 表示100轮放球试验中“每一列至少一个红球”的轮数,统计数据如表:
表示100轮放球试验中“每一列至少一个红球”的轮数,统计数据如表:
求y关于n的回归方程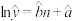 ,并预测
,并预测 时,y的值;(精确到1)
时,y的值;(精确到1)
(2)若 ,
, ,
, ,
,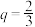 ,记在每列都有白球的条件下,含红球的行数为随机变量
,记在每列都有白球的条件下,含红球的行数为随机变量 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(3)求事件“不是每一列都至少一个红球”发生的概率,并证明: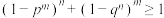 .
.
附:经验回归方程系数: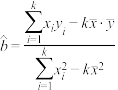 ,
, ,
,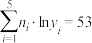 ,
, .
.
 个小正方形构成长方形网格有
个小正方形构成长方形网格有 行和
行和 列.每次将一个小球放到一个小正方形内,放满为止,记为一轮.每次放白球的频率为
列.每次将一个小球放到一个小正方形内,放满为止,记为一轮.每次放白球的频率为 ,放红球的概率为q,
,放红球的概率为q, .
.(1)若
 ,
, ,记
,记 表示100轮放球试验中“每一列至少一个红球”的轮数,统计数据如表:
表示100轮放球试验中“每一列至少一个红球”的轮数,统计数据如表:| n | 1 | 2 | 3 | 4 | 5 |
| y | 76 | 56 | 42 | 30 | 26 |
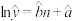 ,并预测
,并预测 时,y的值;(精确到1)
时,y的值;(精确到1)(2)若
 ,
, ,
, ,
,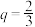 ,记在每列都有白球的条件下,含红球的行数为随机变量
,记在每列都有白球的条件下,含红球的行数为随机变量 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(3)求事件“不是每一列都至少一个红球”发生的概率,并证明:
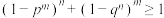 .
.附:经验回归方程系数:
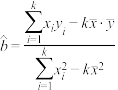 ,
, ,
,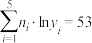 ,
, .
.
您最近一年使用:0次
2023-01-15更新
|
3048次组卷
|
11卷引用:广东省广州市第六中学2023-2024学年高二下学期期末考试数学试卷
广东省广州市第六中学2023-2024学年高二下学期期末考试数学试卷(已下线)第八章 成对数据的统计分析(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)专题8.8 成对数据的统计分析全章综合测试卷(提高篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)辽宁省丹东市敬业实验高级中学2023-2024学年高二下学期四月月考数学试卷山东省青岛市2022-2023学年高三上学期期末数学试题重庆市缙云教育联盟2023届高三二模数学试题(已下线)模块八 专题10 以概率与统计为背景的压轴大题江苏省无锡市南菁高级中学2024届高三上学期期末模拟数学试题江西省南昌市第十九中学2023-2024学年高三下学期第一次模拟考试数学试卷广西来宾市忻城县高级中学2024届高三下学期6月热身考试(桂柳压轴卷一)数学试卷(已下线)专题3 变量的相关性、回归分析压轴大题(过关集训)



