名校
解题方法
1 . 柜子里有3双不同的鞋,分别用 ,
, ;
; ,
, ;
;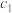 ,
, 表示6只鞋,其中
表示6只鞋,其中 ,
, ,
,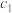 表示每双鞋的左脚,
表示每双鞋的左脚, ,
, ,
, 表示每双鞋的右脚.如果从中随机地取出2只,那么
表示每双鞋的右脚.如果从中随机地取出2只,那么
(1)写出试验的样本空间;
(2)求下列事件的概率:
①取出的鞋都是一只脚的;②取出的鞋子是一只左脚一只右脚的,但不是一双鞋.
(3)求取出的鞋不成双的概率.
 ,
, ;
; ,
, ;
;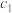 ,
, 表示6只鞋,其中
表示6只鞋,其中 ,
, ,
,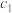 表示每双鞋的左脚,
表示每双鞋的左脚, ,
, ,
, 表示每双鞋的右脚.如果从中随机地取出2只,那么
表示每双鞋的右脚.如果从中随机地取出2只,那么(1)写出试验的样本空间;
(2)求下列事件的概率:
①取出的鞋都是一只脚的;②取出的鞋子是一只左脚一只右脚的,但不是一双鞋.
(3)求取出的鞋不成双的概率.
您最近一年使用:0次
7日内更新
|
124次组卷
|
2卷引用:四川省成都市简阳市成都市简阳实验学校(成都石室阳安学校)2024-2025学年高二上学期10月期中考试数学试题
解题方法
2 . 已知A,B,C三人同时参加对同一个问题竞答;游戏的规则为三人同答一道题,若其中至少一人答对此题,则视为闯过此关.已知此三人答对此题的概率分别为 ,
, ,
, .
.
(1)求此三人闯过此关的概率;
(2)若此三人闯此关时,答对试题的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
 ,
, ,
, .
.(1)求此三人闯过此关的概率;
(2)若此三人闯此关时,答对试题的人数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
您最近一年使用:0次
3 . 一个盒子中有编号为1,2,3,且质地均匀的三枚硬币,第一次取出1号硬币,掷出后记录其得到的是正面或反面.从第二次开始的游戏规则是:①从盒子中剩下的硬币中随机取出一枚,并将上一次取出的硬币放回盒子中;②投掷取出的硬币,记录得到的是正面或反面.
(1)求第三次取出的硬币是1号硬币的概率;
(2)求第三次取出的硬币是2号硬币的概率;
(3)求第五次取出的硬币是1号硬币并投掷得到正面的概率.
(1)求第三次取出的硬币是1号硬币的概率;
(2)求第三次取出的硬币是2号硬币的概率;
(3)求第五次取出的硬币是1号硬币并投掷得到正面的概率.
您最近一年使用:0次
解题方法
4 . 某企业生产手机加密芯片,有3台机器生产同一型号的芯片,质量合格的为正品,不合格的为次品,第1台生产的次品率为 ,第2,3台生产的次品率均为
,第2,3台生产的次品率均为 ,将生产出来的芯片混放在一起,已知第1,2,3台机器生产的芯片数分别占总数的
,将生产出来的芯片混放在一起,已知第1,2,3台机器生产的芯片数分别占总数的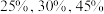 .
.
(1)任取一个芯片,求它是正品的概率;
(2)任取一个芯片,如果它是次品,求它分别是第1,2,3台机器生产的概率.
 ,第2,3台生产的次品率均为
,第2,3台生产的次品率均为 ,将生产出来的芯片混放在一起,已知第1,2,3台机器生产的芯片数分别占总数的
,将生产出来的芯片混放在一起,已知第1,2,3台机器生产的芯片数分别占总数的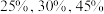 .
.(1)任取一个芯片,求它是正品的概率;
(2)任取一个芯片,如果它是次品,求它分别是第1,2,3台机器生产的概率.
您最近一年使用:0次
名校
5 . 在我校开展的文化节知识竞赛活动中,共有A、B、C三道必答题,答对A、B、C分别得10分,10分,20分,答错不得分.已知甲同学答对问题A、B、C的概率分别为 ,
, ,
, ,乙同学答对问题A、B、C的概率均为
,乙同学答对问题A、B、C的概率均为 ,甲、乙两位同学都回答了这三道题,且各题回答正确与否相互独立.
,甲、乙两位同学都回答了这三道题,且各题回答正确与否相互独立.
(1)求甲同学至少有一道题不能答对的概率;
(2)运用你学过的统计学知识判断,谁的得分能力更强.
 ,
, ,
, ,乙同学答对问题A、B、C的概率均为
,乙同学答对问题A、B、C的概率均为 ,甲、乙两位同学都回答了这三道题,且各题回答正确与否相互独立.
,甲、乙两位同学都回答了这三道题,且各题回答正确与否相互独立.(1)求甲同学至少有一道题不能答对的概率;
(2)运用你学过的统计学知识判断,谁的得分能力更强.
您最近一年使用:0次
名校
解题方法
6 . 目前不少网络媒体都引入了虚拟主播,某视频平台引入虚拟主播 ,在第一天的直播中有超过
,在第一天的直播中有超过 万人次的观看.
万人次的观看.
(1)已知小李第1天观看了虚拟主播 的直播,若小李前一天观看了虚拟主播
的直播,若小李前一天观看了虚拟主播 的直播,则当天观看虚拟主播
的直播,则当天观看虚拟主播 直播的概率为
直播的概率为 ,若前一天没有观看虚拟主播
,若前一天没有观看虚拟主播 的直播,则当天观看虚拟主播
的直播,则当天观看虚拟主播 直播的概率为
直播的概率为 ,求小李第
,求小李第 天和第
天和第 天至少有一天观看虚拟主播直播的概率;
天至少有一天观看虚拟主播直播的概率;
(2)若未来 天内虚拟主播
天内虚拟主播 的直播每天有超过
的直播每天有超过 万人次的观看的概率为
万人次的观看的概率为 ,记这
,记这 天中每天有超过
天中每天有超过 万人次观看的天数为
万人次观看的天数为 .
.
(i)比较 与
与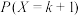 的大小,其中
的大小,其中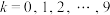 ;
;
(ii)记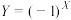 ,求
,求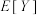 .
.
 ,在第一天的直播中有超过
,在第一天的直播中有超过 万人次的观看.
万人次的观看.(1)已知小李第1天观看了虚拟主播
 的直播,若小李前一天观看了虚拟主播
的直播,若小李前一天观看了虚拟主播 的直播,则当天观看虚拟主播
的直播,则当天观看虚拟主播 直播的概率为
直播的概率为 ,若前一天没有观看虚拟主播
,若前一天没有观看虚拟主播 的直播,则当天观看虚拟主播
的直播,则当天观看虚拟主播 直播的概率为
直播的概率为 ,求小李第
,求小李第 天和第
天和第 天至少有一天观看虚拟主播直播的概率;
天至少有一天观看虚拟主播直播的概率;(2)若未来
 天内虚拟主播
天内虚拟主播 的直播每天有超过
的直播每天有超过 万人次的观看的概率为
万人次的观看的概率为 ,记这
,记这 天中每天有超过
天中每天有超过 万人次观看的天数为
万人次观看的天数为 .
.(i)比较
 与
与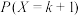 的大小,其中
的大小,其中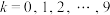 ;
;(ii)记
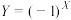 ,求
,求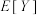 .
.
您最近一年使用:0次
名校
解题方法
7 . 在某抽奖活动中,初始时的袋子中有3个除颜色外其余都相同的小球,颜色为2白1红.每次随机抽取一个小球后放回.抽奖规则如下:设定抽中红球为中奖,抽中白球为未中奖;若抽到白球,放回后把袋中的一个白色小球替换为红色;若抽到红球,放回后把三个球的颜色重新变为2白1红的初始状态.记第n次抽奖中奖的概率为 .
.
(1)求 ,
,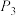 ;
;
(2)若存在实数a,b,c,对任意的不小于4的正整数n,都有 ,试确定a,b,c的值;
,试确定a,b,c的值;
(3)若累计中奖4次及以上可以获得一枚优胜者勋章,则从初始状态下连抽9次获得至少一枚勋章的概率为多少?
 .
.(1)求
 ,
,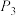 ;
;(2)若存在实数a,b,c,对任意的不小于4的正整数n,都有
 ,试确定a,b,c的值;
,试确定a,b,c的值;(3)若累计中奖4次及以上可以获得一枚优胜者勋章,则从初始状态下连抽9次获得至少一枚勋章的概率为多少?
您最近一年使用:0次
2024-05-22更新
|
192次组卷
|
2卷引用:山东省青岛第一中学2023-2024学年高二下学期第一次模块考试数学试题
名校
8 . 甲、乙、丙三人组队参加某知识问答团体比赛.该比赛共分两轮,第一轮回答错误就直接出局,两轮都回答正确称为“通关”,小组三人中至少有2人“通关”就可获得“团体奖”.根据平时训练和测试可知,甲、乙、丙分别正确回答两轮比赛的概率情况如下表:
若三人各自比赛时互不影响.
(1)求甲、乙两人至少有1人“通关”的概率;
(2)在该三人小组获得“团体奖”的条件下,求甲乙丙同时通关的概率.
| 甲 | 乙 | 丙 | |
| 第一轮回答正确的概率 |  |  |  |
| 第二轮回答正确的概率 |  |  |  |
(1)求甲、乙两人至少有1人“通关”的概率;
(2)在该三人小组获得“团体奖”的条件下,求甲乙丙同时通关的概率.
您最近一年使用:0次
名校
9 . 甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 与p,且乙投球2次均未命中的概率为
与p,且乙投球2次均未命中的概率为 .
.
(1)求乙投球 次的命中率;
次的命中率;
(2)若甲、乙两人各投球 次,求两人共命中
次,求两人共命中 次的概率.
次的概率.
 与p,且乙投球2次均未命中的概率为
与p,且乙投球2次均未命中的概率为 .
.(1)求乙投球
 次的命中率;
次的命中率;(2)若甲、乙两人各投球
 次,求两人共命中
次,求两人共命中 次的概率.
次的概率.
您最近一年使用:0次
名校
解题方法
10 . 将4个形状、大小、颜色均相同的排球随机放入4个编号为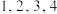 的排球筐内,每个排球筐最多可容纳5个排球,记编号为2的排球筐内最终的排球个数为
的排球筐内,每个排球筐最多可容纳5个排球,记编号为2的排球筐内最终的排球个数为 .
.
(1)求编号为2的排球筐内有球的概率;
(2)求 的分布列.
的分布列.
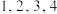 的排球筐内,每个排球筐最多可容纳5个排球,记编号为2的排球筐内最终的排球个数为
的排球筐内,每个排球筐最多可容纳5个排球,记编号为2的排球筐内最终的排球个数为 .
.(1)求编号为2的排球筐内有球的概率;
(2)求
 的分布列.
的分布列.
您最近一年使用:0次



