名校
1 . 某校高一年级设有羽毛球训练课,期末对学生进行羽毛球五项指标(正手发高远球、定点高远球、吊球、杀球以及半场计时往返跑)考核,满分100分.参加考核的学生有40人,考核得分的频率分布直方图如图所示. 的值,并估计考核得分的第60百分位数;
的值,并估计考核得分的第60百分位数;
(2)为了提升同学们的羽毛球技能,校方准备招聘高水平的教练.现采用分层抽样的方法(样本量按比例分配),从得分在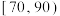 内的学生中抽取5人,再从中挑出两人进行试课,求两人得分分别来自
内的学生中抽取5人,再从中挑出两人进行试课,求两人得分分别来自 和
和 的概率;
的概率;
(3)若一个总体划分为两层,通过按样本量比例分配分层随机抽样,各层抽取的样本量、样本平均数和样本方差分别为: ,
, ,
, ;
; ,
,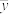 ,
, .记总的样本平均数为
.记总的样本平均数为 ,样本方差为
,样本方差为 ,证明:
,证明: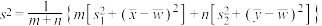 .
.
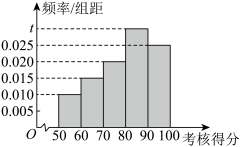
 的值,并估计考核得分的第60百分位数;
的值,并估计考核得分的第60百分位数;(2)为了提升同学们的羽毛球技能,校方准备招聘高水平的教练.现采用分层抽样的方法(样本量按比例分配),从得分在
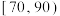 内的学生中抽取5人,再从中挑出两人进行试课,求两人得分分别来自
内的学生中抽取5人,再从中挑出两人进行试课,求两人得分分别来自 和
和 的概率;
的概率;(3)若一个总体划分为两层,通过按样本量比例分配分层随机抽样,各层抽取的样本量、样本平均数和样本方差分别为:
 ,
, ,
, ;
; ,
,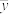 ,
, .记总的样本平均数为
.记总的样本平均数为 ,样本方差为
,样本方差为 ,证明:
,证明: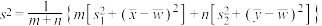 .
.
您最近一年使用:0次
7日内更新
|
424次组卷
|
3卷引用:湖北省恩施州来凤县第一中学2024-2025学年高二上学期10月月考数学试卷
名校
2 . 对于两个平面向量 ,
, ,如果有
,如果有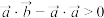 ,则称向量
,则称向量 是向量
是向量 的“迷你向量”.
的“迷你向量”.
(1)若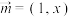 ,
,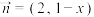 ,
,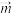 是
是 的“迷你向量”,求实数
的“迷你向量”,求实数 的取值范围;
的取值范围;
(2)一只蚂蚁从坐标原点 沿最短路径爬行到点
沿最短路径爬行到点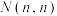 处(
处( 且
且 ).蚂蚁每次只能沿平行或垂直于坐标轴的方向爬行一个单位长度,爬完第
).蚂蚁每次只能沿平行或垂直于坐标轴的方向爬行一个单位长度,爬完第 次后停留的位置记为
次后停留的位置记为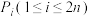 ,设
,设 .记事件
.记事件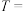 “蚂蚁经过的路径中至少有
“蚂蚁经过的路径中至少有 个
个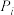 使得
使得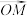 是
是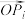 的迷你向量”.(假设蚂蚁选择每条路径都是等可能的)
的迷你向量”.(假设蚂蚁选择每条路径都是等可能的)
①当 时,求
时,求 ;
;
②证明: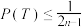 .
.
 ,
, ,如果有
,如果有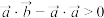 ,则称向量
,则称向量 是向量
是向量 的“迷你向量”.
的“迷你向量”.(1)若
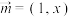 ,
,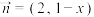 ,
,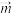 是
是 的“迷你向量”,求实数
的“迷你向量”,求实数 的取值范围;
的取值范围;(2)一只蚂蚁从坐标原点
 沿最短路径爬行到点
沿最短路径爬行到点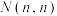 处(
处( 且
且 ).蚂蚁每次只能沿平行或垂直于坐标轴的方向爬行一个单位长度,爬完第
).蚂蚁每次只能沿平行或垂直于坐标轴的方向爬行一个单位长度,爬完第 次后停留的位置记为
次后停留的位置记为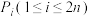 ,设
,设 .记事件
.记事件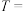 “蚂蚁经过的路径中至少有
“蚂蚁经过的路径中至少有 个
个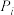 使得
使得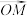 是
是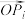 的迷你向量”.(假设蚂蚁选择每条路径都是等可能的)
的迷你向量”.(假设蚂蚁选择每条路径都是等可能的)①当
 时,求
时,求 ;
;②证明:
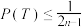 .
.
您最近一年使用:0次
2024-07-03更新
|
515次组卷
|
2卷引用:湖北省武汉市华中师范大学第一附属中学2023-2024学年高一下学期7月期末检测数学试题
名校
解题方法
3 . 某情报站有 .五种互不相同的密码,每周使用其中的一种密码,且每周都是从上周末使用的四种密码中等可能地随机选用一种.设第一周使用
.五种互不相同的密码,每周使用其中的一种密码,且每周都是从上周末使用的四种密码中等可能地随机选用一种.设第一周使用 密码,
密码,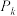 表示第
表示第 周使用
周使用 密码的概率.
密码的概率.
(1)求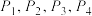 ;
;
(2)求证: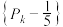 为等比数列,并求
为等比数列,并求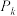 的表达式.
的表达式.
 .五种互不相同的密码,每周使用其中的一种密码,且每周都是从上周末使用的四种密码中等可能地随机选用一种.设第一周使用
.五种互不相同的密码,每周使用其中的一种密码,且每周都是从上周末使用的四种密码中等可能地随机选用一种.设第一周使用 密码,
密码,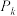 表示第
表示第 周使用
周使用 密码的概率.
密码的概率.(1)求
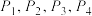 ;
;(2)求证:
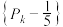 为等比数列,并求
为等比数列,并求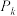 的表达式.
的表达式.
您最近一年使用:0次
2022-01-26更新
|
734次组卷
|
2卷引用:湖北省2021-2022学年高二上学期期末调考数学试题
真题
名校
4 . 近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下(单位:吨):
(Ⅰ)试估计厨余垃圾投放正确的概率
(Ⅱ)试估计生活垃圾投放错误的概率
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c,的方差 最大时,写出a,b,c的值(结论不要求证明),并求此时
最大时,写出a,b,c的值(结论不要求证明),并求此时 的值.
的值.
(注: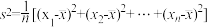 ,其中
,其中 为数据
为数据 的平均数)
的平均数)
| “厨余垃圾”箱 | “可回收物”箱 | “其他垃圾”箱 | |
| 厨余垃圾 | 400 | 100 | 100 |
| 可回收物 | 30 | 240 | 30 |
| 其他垃圾 | 20 | 20 | 60 |
(Ⅰ)试估计厨余垃圾投放正确的概率
(Ⅱ)试估计生活垃圾投放错误的概率
(Ⅲ)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c,的方差
 最大时,写出a,b,c的值(结论不要求证明),并求此时
最大时,写出a,b,c的值(结论不要求证明),并求此时 的值.
的值.(注:
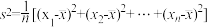 ,其中
,其中 为数据
为数据 的平均数)
的平均数)
您最近一年使用:0次
2019-01-30更新
|
2503次组卷
|
9卷引用:2012-2013学年湖北省黄冈中学高二上学期期中考试理科数学试卷
名校
解题方法
5 . 暑假期间小辉计划在8月11日至8月20日期间调研某商业中心周边停车场停车状况,根据停车场统计数据,该停车场在此期间“停车难易度”(即停车数量与核定的最大瞬时容量之比,40%以下为较易,40%~60%为一般,60%以上为较难),情况如图所示,小辉随机选择8月11日至8月19日中的某一天达到该商业中心,并连续调研2天.
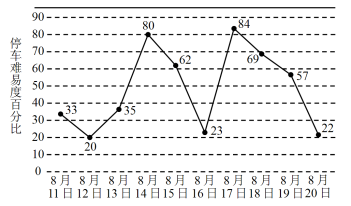
(1)求小辉连续两天都遇上停车场较难的概率;
(2)设 是小辉调研期间遇上停车较易的天数,求
是小辉调研期间遇上停车较易的天数,求 的分布列和数学期望;
的分布列和数学期望;
(3)由图判断从哪天开始连续三天停车难易度的方差最大?(结论不要求证明)

(1)求小辉连续两天都遇上停车场较难的概率;
(2)设
 是小辉调研期间遇上停车较易的天数,求
是小辉调研期间遇上停车较易的天数,求 的分布列和数学期望;
的分布列和数学期望;(3)由图判断从哪天开始连续三天停车难易度的方差最大?(结论不要求证明)
您最近一年使用:0次
2014·全国·一模
解题方法
6 . 如图是某市3月1日至14日的空气质量指数趋势图.空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
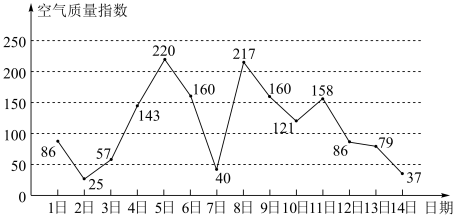
(1)求3月1日到14日空气质量指数的中位数;
(2)求此人到达当日空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)

(1)求3月1日到14日空气质量指数的中位数;
(2)求此人到达当日空气重度污染的概率;
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
您最近一年使用:0次
2016-12-03更新
|
1508次组卷
|
3卷引用:湖北省天门、仙桃、潜江2018届高三上学期期末联考数学(文)试题



