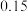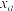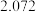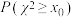名校
解题方法
1 . 某大学组织宣传小分队进行法律法规宣传,某宣传小分队记录了前9天每天普及的人数,得到下表:
(1)从这9天的数据中任选2天的数据,以X表示2天中普及人数不少于200人的天数,求X的分布列和数学期望;
(2)由于统计人员的疏忽,第5天的数据统计有误,如果去掉第5天的数据,试用剩下的数据求出每天普及的人数y关于天数x的线性回归方程.
参考数据: ,
, ,
, .附:对于一组数据(
.附:对于一组数据( ,
, ),(
),( ,
, ),……,(
),……,( ,
, ),其回归直线
),其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: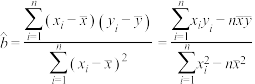 ,
, .
.
| 时间x(天) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 每天普及的人数y | 80 | 98 | 129 | 150 | 203 | 190 | 258 | 292 | 310 |
(2)由于统计人员的疏忽,第5天的数据统计有误,如果去掉第5天的数据,试用剩下的数据求出每天普及的人数y关于天数x的线性回归方程.
参考数据:
 ,
, ,
, .附:对于一组数据(
.附:对于一组数据( ,
, ),(
),( ,
, ),……,(
),……,( ,
, ),其回归直线
),其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: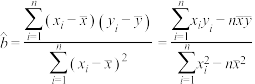 ,
, .
.
您最近一年使用:0次
2024-08-23更新
|
114次组卷
|
3卷引用:江苏省南通一中2023-2024学年高二年级数学下学期第二次月考(含答案)
江苏省南通一中2023-2024学年高二年级数学下学期第二次月考(含答案)黑龙江省哈尔滨市第四中学校2023-2024学年高二下学期期末考试数学试卷(已下线)专题2 回归方程 拟合效果(经典好题母题)【练】
名校
2 . 某学校为提高学生身体素质,号召全校学生参加体育锻炼,结合每日统计的运动情况,对每日平均运动10000步或以上的学生授予“运动达人”称号,低于10000步称为“参与者”,统计了200名学生在某月的运动数据,结果如下:
(1)完善 列联表并说明:是否有
列联表并说明:是否有 的把握认为获得“运动达人”称号与性别有关?
的把握认为获得“运动达人”称号与性别有关?
(2)从全校“运动达人”中按性别分层抽取8人,再从8人中选取3人参加特训,将特训的人中男生人数记为 ,求
,求 的分布列与均值
的分布列与均值 .
.
参考公式: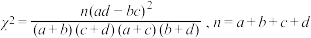
运动达人 | 参与者 | 合计 | |
男生 | 70 | ||
女生 | 80 | ||
合计 | 80 | 200 |
 列联表并说明:是否有
列联表并说明:是否有 的把握认为获得“运动达人”称号与性别有关?
的把握认为获得“运动达人”称号与性别有关?(2)从全校“运动达人”中按性别分层抽取8人,再从8人中选取3人参加特训,将特训的人中男生人数记为
 ,求
,求 的分布列与均值
的分布列与均值 .
.参考公式:
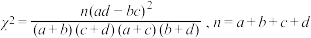
|
|
|
|
|
|
|
|
|
|
|
|
| 10.828 |
您最近一年使用:0次
解题方法
3 . 下列命题正确的是( )
A.若随机变量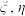 满足 满足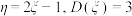 ,则 ,则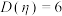 |
B.若 ,则 ,则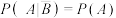 |
C.若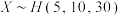 ,则 ,则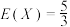 |
D.若 分布, 分布,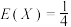 ,则 ,则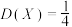 |
您最近一年使用:0次
解题方法
4 . 已知20条试题中有8条选择题,甲无放回地依次从中抽取5条题,乙有放回地依次从中抽取5条题,甲、乙每次均抽取一条试题,抽出的5条题中选择题的条数分别为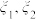 ,
,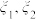 的期望分别为
的期望分别为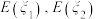 ,方差分别为
,方差分别为 ,则( )
,则( )
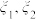 ,
,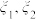 的期望分别为
的期望分别为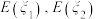 ,方差分别为
,方差分别为 ,则( )
,则( )A.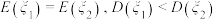 | B.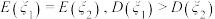 |
C.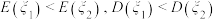 | D.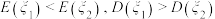 |
您最近一年使用:0次
名校
解题方法
5 . 袋中有6个大小相同的球,其中4个黑球,2个白球,现从中任取3个球,记随机变量 为其中白球的个数,随机变量
为其中白球的个数,随机变量 为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量
为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量 为取出3个球的总得分,则下列结论正确的是( )
为取出3个球的总得分,则下列结论正确的是( )
 为其中白球的个数,随机变量
为其中白球的个数,随机变量 为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量
为其中黑球的个数,若取出一个白球得2分,取出一个黑球得1分,随机变量 为取出3个球的总得分,则下列结论正确的是( )
为取出3个球的总得分,则下列结论正确的是( )A. | B. |
C. | D. |
您最近一年使用:0次
名校
解题方法
6 . 某社区为了推动全民健身,增加人们对体育运动的兴趣,随机抽取了男,女各 200 人做 统计调查. 统计显示,被调查的人中,喜欢运动的男性有 100 人,不喜欢运动的女性有 50 人.
(1)完成下面列联表,并判断能否在犯错误概率不超过 0.005的情况下认为人们喜欢运动与性别有关;
(2)为了鼓励全民运动,社区开展一次趣味体育比赛,并设置3个奖项,每个奖项有且仅有 一人获取,每人最多只能获得 1 个奖项; 现从这 400 人中选出男性4人,女性4人参加 比赛,记 为获奖的男性人数,求
为获奖的男性人数,求 的分布列和数学期望.
的分布列和数学期望.
附:
(1)完成下面列联表,并判断能否在犯错误概率不超过 0.005的情况下认为人们喜欢运动与性别有关;
喜欢 | 不喜欢 | 合计 | |
男性 | |||
女性 | |||
合计 |
 为获奖的男性人数,求
为获奖的男性人数,求 的分布列和数学期望.
的分布列和数学期望.附:

| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-05-27更新
|
416次组卷
|
2卷引用:江苏省如皋中学2023-2024学年高二下学期教学质量调研(二)数学试题
名校
7 . 某城市人口数量950万人左右,共900个社区.在实施垃圾分类之前,随机抽取300个社区,并对这300个社区某天产生的垃圾量(单位:吨)进行了调查,每个社区在这一天的垃圾量X大致服从正态分布 .将垃圾量超过32吨
.将垃圾量超过32吨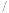 天的社区确定为“超标”社区.
天的社区确定为“超标”社区.
(1)请利用正态分布知识估计这900个社区中“超标”社区的个数;(结果取整数部分)
(2)通过研究样本原始数据发现,抽取的300个社区中这一天共有7个“超标”社区,市政府决定对7个“超标”社区的垃圾来源进行跟踪调查.现计划在这7个“超标”社区中任取4个进行跟踪调查,已知这7个社区中有3个社区在这一天的垃圾量超过35吨.设 为抽到的这一天的垃圾量超过35吨的社区个数,求
为抽到的这一天的垃圾量超过35吨的社区个数,求 的概率分布与数学期望;
的概率分布与数学期望;
(3)用样本的频率代替总体的概率,现从该市所有社区中随机抽取50个社区,记 为这一天垃圾量超过32吨的小区的个数,求
为这一天垃圾量超过32吨的小区的个数,求 的值.
的值.
(参考数据: ;
;  ;
; ;
; )
)
 .将垃圾量超过32吨
.将垃圾量超过32吨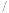 天的社区确定为“超标”社区.
天的社区确定为“超标”社区.(1)请利用正态分布知识估计这900个社区中“超标”社区的个数;(结果取整数部分)
(2)通过研究样本原始数据发现,抽取的300个社区中这一天共有7个“超标”社区,市政府决定对7个“超标”社区的垃圾来源进行跟踪调查.现计划在这7个“超标”社区中任取4个进行跟踪调查,已知这7个社区中有3个社区在这一天的垃圾量超过35吨.设
 为抽到的这一天的垃圾量超过35吨的社区个数,求
为抽到的这一天的垃圾量超过35吨的社区个数,求 的概率分布与数学期望;
的概率分布与数学期望;(3)用样本的频率代替总体的概率,现从该市所有社区中随机抽取50个社区,记
 为这一天垃圾量超过32吨的小区的个数,求
为这一天垃圾量超过32吨的小区的个数,求 的值.
的值.(参考数据:
 ;
;  ;
; ;
; )
)
您最近一年使用:0次
2024-05-25更新
|
1180次组卷
|
4卷引用:江苏省南京市六校联合体学校2023-2024学年高二下学期5月月考数学试题
江苏省南京市六校联合体学校2023-2024学年高二下学期5月月考数学试题(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)山东省菏泽市定陶区第一中学2023-2024学年高二下学期5月月考数学试题河北省唐县第一中学2023-2024学年高二下学期6月期末数学试题
名校
8 . 为深入推进传统制造业改造提升,依靠创新引领产业升级,某设备生产企业对现有生产设备进行技术攻坚突破.设备生产的零件的直径为X(单位:nm).
(1)现有旧设备生产的零件有10个,其中直径大于10nm的有2个.现从这10个零件中随机抽取3个.记 表示取出的零件中直径大于10nm的零件的个数,求
表示取出的零件中直径大于10nm的零件的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;
(2)技术攻坚突破后设备生产的零件的合格率为 ,每个零件是否合格相互独立.现任取4个零件进行检测,若合格的零件数
,每个零件是否合格相互独立.现任取4个零件进行检测,若合格的零件数 超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及
超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及 的方差;
的方差;
(3)若技术攻坚后新设备生产的零件直径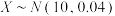 ,从生产的零件中随机取出10个,求至少有一个零件直径大于10.4nm的概率.
,从生产的零件中随机取出10个,求至少有一个零件直径大于10.4nm的概率.
参考数据:若 ,则
,则 ,
,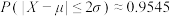 ,
,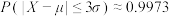 ,
,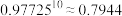 ,
,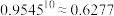 .
.
(1)现有旧设备生产的零件有10个,其中直径大于10nm的有2个.现从这10个零件中随机抽取3个.记
 表示取出的零件中直径大于10nm的零件的个数,求
表示取出的零件中直径大于10nm的零件的个数,求 的分布列及数学期望
的分布列及数学期望 ;
;(2)技术攻坚突破后设备生产的零件的合格率为
 ,每个零件是否合格相互独立.现任取4个零件进行检测,若合格的零件数
,每个零件是否合格相互独立.现任取4个零件进行检测,若合格的零件数 超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及
超过半数,则可认为技术攻坚成功.求技术攻坚成功的概率及 的方差;
的方差;(3)若技术攻坚后新设备生产的零件直径
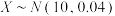 ,从生产的零件中随机取出10个,求至少有一个零件直径大于10.4nm的概率.
,从生产的零件中随机取出10个,求至少有一个零件直径大于10.4nm的概率.参考数据:若
 ,则
,则 ,
,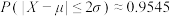 ,
,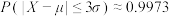 ,
,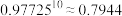 ,
,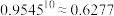 .
.
您最近一年使用:0次
2024-05-12更新
|
948次组卷
|
6卷引用:江苏省泰州中学2023-2024学年高二下学期期中考试数学试题
名校
9 . 某学校号召学生参加“每天锻炼1小时”活动,为了解学生参加活动的情况,统计了全校所有学生在假期每周锻炼的时间,现随机抽取了60名同学在某一周参加锻炼的数据,整理如下 列联表:
列联表:
注:将一周参加锻炼时间不小于3小时的称为“经常锻炼”,其余的称为“不经常锻炼”.
(1)请完成上面 列联表,并依据小概率值
列联表,并依据小概率值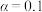 的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;
的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;
(2)将一周参加锻炼为0小时的称为“极度缺乏锻炼”.在抽取的60名同学中有5人“极度缺乏锻炼”.以样本频率估计概率.若在全校抽取20名同学,设“极度缺乏锻炼”的人数为X,求X的数学期望 和方差
和方差 ;
;
(3)将一周参加锻炼6小时以上的同学称为“运动爱好者”.在抽取的60名同学中有10名“运动爱好者”,其中有7名男生,3名女生.为进一步了解他们的生活习惯,在10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为Y,求Y的分布列和数学期望.
附: ,
,
 列联表:
列联表:性别 | 不经常锻炼 | 经常锻炼 | 合计 |
男生 | 7 | ||
女生 | 16 | 30 | |
合计 | 21 |
(1)请完成上面
 列联表,并依据小概率值
列联表,并依据小概率值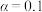 的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;
的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;(2)将一周参加锻炼为0小时的称为“极度缺乏锻炼”.在抽取的60名同学中有5人“极度缺乏锻炼”.以样本频率估计概率.若在全校抽取20名同学,设“极度缺乏锻炼”的人数为X,求X的数学期望
 和方差
和方差 ;
;(3)将一周参加锻炼6小时以上的同学称为“运动爱好者”.在抽取的60名同学中有10名“运动爱好者”,其中有7名男生,3名女生.为进一步了解他们的生活习惯,在10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为Y,求Y的分布列和数学期望.
附:
 ,
,
| 0.1 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2024-05-09更新
|
1767次组卷
|
12卷引用:江苏省盐城中学、南京二十九中联考2023-2024学年高二下学期4月期中数学试题
江苏省盐城中学、南京二十九中联考2023-2024学年高二下学期4月期中数学试题江苏省苏州实验中学2023-2024学年高二下学期5月月考数学试题江苏省淮安市洪泽中学,金湖中学,清河中学,清浦中学等学校2023-2024学年高二下学期5月月考数学试题(已下线)专题07 回归方程与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)湖北省部分重点中学2023-2024学年高二下学期五月联考数学试卷广东省江门市鹤山市第一中学2023-2024学年高二下学期第二阶段考试(5月)数学试题山东省滕州市第五中学2023-2024学年高二下学期第四次单元检测(第二次月考)数学试题福建省福州市闽侯县第一中学2023-2024学年高二下学期第二次月考(5月)数学试题辽宁省七校协作体2023-2024学年高二下学期6月月考数学试题江西省南昌市第十中学2023-2024学年高二下学期第二次月考数学试题黑龙江省哈尔滨市双城区兆麟中学2023-2024学年高二下学期第二次月考(6月)数学试题(已下线)第1套 期末全真模拟卷(高二期末中等卷)
名校
10 . 2024年1月4日,教育部在京召开全国“双减”工作视频调度会,会议要求进一步提高双减政治站位,将“双减”工作作为重中之重,坚定不移推进,成为受老师和家长关注的重要话题.某学校为了解家长对双减工作的满意程度进行问卷调查(评价结果仅有“满意”、“不满意”),从所有参与评价的对象中随机抽取120人进行调查,部分数据如表所示(单位:人):
(1)请将 列联表补充完整,试根据小概率值
列联表补充完整,试根据小概率值 的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
(2)若将频率视为概率,从所有给出“满意”的家长中随机抽取3人,用随机变量 表示被抽到的男性家长的人数,求
表示被抽到的男性家长的人数,求 的分布列;
的分布列;
(3)在抽出的120人中,从给出“满意”的家长中利用分层抽样的方法抽取10人,从给出“不满意”的对象中抽取 人.现从这
人.现从这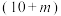 人中,随机抽出2人,用随机变量
人中,随机抽出2人,用随机变量 表示被抽到的给出“满意”的女性家长的人数.若随机变量
表示被抽到的给出“满意”的女性家长的人数.若随机变量 的数学期望不小于1,求
的数学期望不小于1,求 的最大值.
的最大值.
参考公式: ,其中
,其中 .
.
参考数据:
满意 | 不满意 | 合计 | |
男性 | 10 | 50 | |
女性 | 60 | ||
合计 | 120 |
 列联表补充完整,试根据小概率值
列联表补充完整,试根据小概率值 的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?
的独立性检验,能否认为“对双减工作满意程度的评价与性别有关”?(2)若将频率视为概率,从所有给出“满意”的家长中随机抽取3人,用随机变量
 表示被抽到的男性家长的人数,求
表示被抽到的男性家长的人数,求 的分布列;
的分布列;(3)在抽出的120人中,从给出“满意”的家长中利用分层抽样的方法抽取10人,从给出“不满意”的对象中抽取
 人.现从这
人.现从这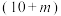 人中,随机抽出2人,用随机变量
人中,随机抽出2人,用随机变量 表示被抽到的给出“满意”的女性家长的人数.若随机变量
表示被抽到的给出“满意”的女性家长的人数.若随机变量 的数学期望不小于1,求
的数学期望不小于1,求 的最大值.
的最大值.参考公式:
 ,其中
,其中 .
.参考数据:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-05-08更新
|
738次组卷
|
5卷引用:专题07 回归方程与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)
(已下线)专题07 回归方程与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)吉林省长春市第八中学2023-2024学年高二下学期第一次月考数学试题(已下线)第八章:成对数据的统计分析章末综合检测卷(新题型)-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)河南省百师联盟联考2023-2024学年高二下学期6月联考数学试题吉林省长春市文理高中2023-2024学年高二下学期5月月考数学试题