名校
1 . 一个池塘里的鱼的数目记为N,从池塘里捞出200尾鱼,并给鱼作上标识,然后把鱼放回池塘里,过一小段时间后再从池塘里捞出500尾鱼, 表示捞出的500尾鱼中有标识的鱼的数目.
表示捞出的500尾鱼中有标识的鱼的数目.
(1)若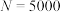 ,求
,求 的数学期望;
的数学期望;
(2)已知捞出的500尾鱼中15尾有标识,试给出N的估计值(以使得 最大的N的值作为N的估计值).
最大的N的值作为N的估计值).
 表示捞出的500尾鱼中有标识的鱼的数目.
表示捞出的500尾鱼中有标识的鱼的数目.(1)若
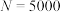 ,求
,求 的数学期望;
的数学期望;(2)已知捞出的500尾鱼中15尾有标识,试给出N的估计值(以使得
 最大的N的值作为N的估计值).
最大的N的值作为N的估计值).
您最近一年使用:0次
2023-02-23更新
|
6489次组卷
|
12卷引用:云南省2023届高三第一次高中毕业生复习统一检测数学试题
云南省2023届高三第一次高中毕业生复习统一检测数学试题2023届安徽省、云南省、吉林省、黑龙江省高三下学期2月适应性测试数学试题2023年安徽省、云南省、吉林省、黑龙江省联考数学试卷评价(已下线)2023年四省联考变试题17-22山西省大同市2023届高三阶段性模拟(2月联考)数学试题(A卷)(已下线)专题18计数原理与概率统计(解答题)陕西省宝鸡市千阳县中学2023届高三第十二次模考理科数学试题山西省大同市第一中学校等2校2023届高三一模理科数学试题(已下线)江西省九师联盟2024届高三上学期10月联考数学试题(已下线)微考点7-1 分布列概率中的三大最值问题(三大题型)山东师范大学附属中学2024届高三下学期考前适应性测试数学试题福建省漳州市龙文区2024届高三6月模拟预测数学试题
名校
2 . 在某校举办“青春献礼二十大,强国有我新征程”的知识能力测评中,随机抽查了100名学生,其中共有4名女生和3名男生的成绩在90分以上,从这7名同学中每次随机抽1人在全校作经验分享,每位同学最多分享一次,记第一次抽到女生为事件A,第二次抽到男生为事件B.
(1)求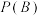 ,
, ,
,
(2)若把抽取学生的方式更改为:从这7名学生中随机抽取3人进行经验分享,记被抽取的3人中女生的人数为X,求X的分布列和数学期望.
(1)求
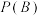 ,
, ,
,(2)若把抽取学生的方式更改为:从这7名学生中随机抽取3人进行经验分享,记被抽取的3人中女生的人数为X,求X的分布列和数学期望.
您最近一年使用:0次
2023-02-15更新
|
2597次组卷
|
13卷引用:云南省红河州2023届高三第一次复习统一检测(一模)数学试题
云南省红河州2023届高三第一次复习统一检测(一模)数学试题(已下线)模块十 计数原理与统计概率-1(已下线)7.4 二项分布与超几何分布(练习)(已下线)8.2.3-8.2.4二项分布 超几何分布(练习)(已下线)第8章 概率 单元综合检测(练习)(已下线)专题18计数原理与概率统计(解答题)黑龙江省大庆市大庆实验中学2022-2023学年高二下学期4月月考数学试题(已下线)随机变量及其分布章末检测卷(一)-【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第三册)(已下线)第6章 计数原理(A卷·知识通关练)(3)(已下线)第7章 概率初步(续)(A卷·知识通关练)(2)吉林省“BEST合作体”2022-2023学年高二下学期期末联考数学试题黑龙江省鸡西市鸡冠区鸡西实验中学2022-2023学年高二下学期期末数学试题湖北省荆州市松滋市第一中学2024届高三上学期12月月考模拟数学试题(二)
名校
解题方法
3 . 端午节吃粽子是我国的传统习俗,设一盘中装有10个粽子,其中豆沙粽2个,白粽8个,这两种粽子的外观完全相同,从中任意选取3个.
(1)求既有豆沙粽又有白粽的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
(1)求既有豆沙粽又有白粽的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
您最近一年使用:0次
2023-03-26更新
|
2517次组卷
|
9卷引用:云南省曲靖市兴教学校2022-2023学年高二下学期期中数学试题
云南省曲靖市兴教学校2022-2023学年高二下学期期中数学试题北京市朝阳区东北师范大学附属中学朝阳学校2022-2023学年高二下学期第一次质量监测与反馈数学试题吉林省长春市十一高中2022-2023学年高二下学期第一学程考试数学试题广西柳州地区民族高级中学2022-2023学年高二下学期期中考试数学试题湖南省怀化市第五中学2022-2023学年高二下学期期中数学试题广西钦州市灵山县那隆中学2022-2023学年高二下学期期中数学试题新疆哈密市第八中学2022-2023学年高二下学期期中考试数学试题(已下线)拓展三:二项分布和超几何分布辨析 -【帮课堂】2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第三册)新疆维吾尔自治区喀什地区喀什市2022-2023学年高二下学期期中质量监测数学试题
名校
4 . 某公司为监督检查下属的甲、乙两条生产线所生产产品的质量,分别从甲、乙两条生产线出库的产品中各随机抽取了100件产品,并对所抽取产品进行检验,检验后发现,甲生产线的合格品占八成、优等品占两成,乙生产线的合格品占九成、优等品占一成(合格品与优等品间无包含关系).
(1)用分层随机抽样的方法从样品的优等品中抽取6件产品,在这6件产品中随机抽取2件,记这2件产品中来自甲生产线的产品个数有 个,求
个,求 的分布列与数学期望;
的分布列与数学期望;
(2)消费者对该公司产品的满意率为 ,随机调研5位购买过该产品的消费者,记对该公司产品满意的人数有
,随机调研5位购买过该产品的消费者,记对该公司产品满意的人数有 人,求至少有3人满意的概率及
人,求至少有3人满意的概率及 的数学期望与方差.
的数学期望与方差.
(1)用分层随机抽样的方法从样品的优等品中抽取6件产品,在这6件产品中随机抽取2件,记这2件产品中来自甲生产线的产品个数有
 个,求
个,求 的分布列与数学期望;
的分布列与数学期望;(2)消费者对该公司产品的满意率为
 ,随机调研5位购买过该产品的消费者,记对该公司产品满意的人数有
,随机调研5位购买过该产品的消费者,记对该公司产品满意的人数有 人,求至少有3人满意的概率及
人,求至少有3人满意的概率及 的数学期望与方差.
的数学期望与方差.
您最近一年使用:0次
2024-05-28更新
|
847次组卷
|
8卷引用:云南省昭通市水富市第一中学2023-2024学年高二下学期第三次月考(5月)数学试题
云南省昭通市水富市第一中学2023-2024学年高二下学期第三次月考(5月)数学试题安徽省蒙城县第六中学2023-2024学年高二下学期阶段性考试数学试题(已下线)专题04 随机变量及其分布类常考题型归类--高二期末考点大串讲(人教B版2019选择性必修第二册)(已下线)核心考点7 二项分布与超几何分布、正态分布 B提升卷 (高二期末考试必考的10大核心考点)安徽省滁州市九校2023-2024学年高二下学期4月期中联考数学试题(已下线)第1套 考前押题卷(高二期末)福建省福州市六校2023-2024学年高二下学期期末联考数学试题(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点2 重要的概率分布模型(二)【基础版】
名校
5 . 2023年冬,甲型流感病毒来势汹汹.某科研小组经过研究发现,患病者与未患病者的某项医学指标有明显差异.在某地的两类人群中各随机抽取20人的该项医学指标作为样本,得到如下的患病者和未患病者该指标的频率分布直方图: ,将该指标小于
,将该指标小于 的人判定为阳性,大于或等于
的人判定为阳性,大于或等于 的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为
的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为 ;误诊率是将未患病者判定为阳性的概率,记为
;误诊率是将未患病者判定为阳性的概率,记为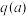 .假设数据在组内均匀分布,用频率估计概率.
.假设数据在组内均匀分布,用频率估计概率.
(1)当临界值 时,求漏诊率
时,求漏诊率 和误诊率
和误诊率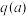 ;
;
(2)从指标在区间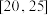 样本中随机抽取2人,记随机变量
样本中随机抽取2人,记随机变量 为未患病者的人数,求
为未患病者的人数,求 的分布列和数学期望;
的分布列和数学期望;
(3)在该地患病者占全部人口的5%的情况下,记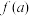 为该地诊断结果不符合真实情况的概率.当
为该地诊断结果不符合真实情况的概率.当 时,直接写出使得
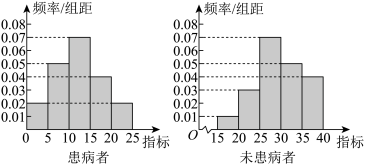
时,直接写出使得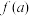 取最小值时的
取最小值时的 的值.
的值.
 ,将该指标小于
,将该指标小于 的人判定为阳性,大于或等于
的人判定为阳性,大于或等于 的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为
的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为 ;误诊率是将未患病者判定为阳性的概率,记为
;误诊率是将未患病者判定为阳性的概率,记为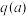 .假设数据在组内均匀分布,用频率估计概率.
.假设数据在组内均匀分布,用频率估计概率.(1)当临界值
 时,求漏诊率
时,求漏诊率 和误诊率
和误诊率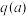 ;
;(2)从指标在区间
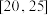 样本中随机抽取2人,记随机变量
样本中随机抽取2人,记随机变量 为未患病者的人数,求
为未患病者的人数,求 的分布列和数学期望;
的分布列和数学期望;(3)在该地患病者占全部人口的5%的情况下,记
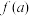 为该地诊断结果不符合真实情况的概率.当
为该地诊断结果不符合真实情况的概率.当 时,直接写出使得
时,直接写出使得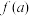 取最小值时的
取最小值时的 的值.
的值.
您最近一年使用:0次
2024-01-22更新
|
766次组卷
|
4卷引用:云南省大理白族自治州民族中学2023-2024学年高三下学期5月月考数学试卷
云南省大理白族自治州民族中学2023-2024学年高三下学期5月月考数学试卷北京市丰台区2023-2024学年高三上学期期末练习数学试卷(已下线)第七章 随机变量及其分布(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)四川省雅安市神州天立学校2024届高三下学期高考冲刺热身(四)数学(理)试题
6 . 甲、乙去某公司应聘面试.该公司的面试方案为:应聘者从6道备选题中一次性随机抽取3道题,按照答对题目的个数为标准进行筛选.已知6道备选题中应聘者甲有4道题能正确完成,2道题不能完成;应聘者乙每题正确完成的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大?
 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性较大?
您最近一年使用:0次
2019-09-18更新
|
3829次组卷
|
29卷引用:云南省名校2019-2020学年高考适应性月考统一考试数学(理)试题
云南省名校2019-2020学年高考适应性月考统一考试数学(理)试题(已下线)2014届北京市昌平区高三年级第二次统一练习数学试卷2015届甘肃省天水市一中高三高考信息卷一理科数学试卷广东省中山市2016-2017学年高二下学期期末统一考试数学(理)试题山东省枣庄市第八中学东校区2016-2017学年高二5月月考数学(理)试题【全国百强校】福建省上杭县第一中学2017-2018学年高二下学期第二次月考(6月)数学(理)试题甘肃省兰州市第一中学2018-2019学年高二下学期期末数学(理)试题江西省上高二中2018-2019学年高二下学期期末数学(理)试题湖南省长沙市长郡中学2018-2019学年高二下学期期末考试数学(理)试题广东省云浮市2019-2020学年高二下学期期末数学试题人教A版(2019) 必修第二册 第十章 概率 单元测试(已下线)7.4 二项分布与超几何分布(精讲)-2020-2021学年高二数学一隅三反系列(人教A版2019选择性必修第三册)(已下线)专题09 计数原理与概率统计-【备战高考】2021年高三数学高考复习刷题宝典(解答题专练)(已下线)专题11 随机变量及其应用-备战2021年高考数学二轮复习题型专练(新高考专用)辽宁省辽南协作校2020-2021学年高二上学期期末数学试题辽宁省抚顺二中、沈阳二中等2020-2021学年高二上学期期末考试数学试题新疆乌鲁木齐市第八中学2020-2021学年高二下学期第一阶段考试数学(理)试题人教A版(2019) 选修第三册 过关斩将 期末学业水平检测重庆市江津第五中学校2021-2022学年高二下学期期中数学试题安徽省滁州市定远县育才学校2021-2022学年高一下学期期末考试数学试题(已下线)专题22 二项分布、超几何分布(重点突围)-【学霸满分】2022-2023学年高二数学下学期重难点专题提优训练(苏教版2019选择性必修第二册)福建省石狮市永宁中学(厦外石分永宁校区)2022-2023学年高二下学期期末考试数学试题广东省深圳市云顶学校高中部2022-2023学年高二下学期期中数学试题(已下线)第11讲 二项分布与超几何分布-【寒假预科讲义】2024年高二数学寒假精品课(人教A版2019)(已下线)专题7.4 二项分布与超几何分布【八大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)7.4.2超几何分布 第三练 能力提升拔高【人教A版(2019)】专题15概率与统计(第五部分)-高二下学期名校期末好题汇编广东省东莞市光正实验学校2023-2024学年高三上学期第一次月考数学试题
名校
解题方法
7 . 春节期间某网络支付平台开展集“福”字活动:共有5种不同的“福”字电子卡,每完成一笔网络支付交易就能随机获赠一张“福”字卡,集齐5张不同的“福”字卡即可获奖.某网购平台上购买一袋脆干面,内随赠一张水浒传一百单八将的好汉卡,集齐完整一套好汉卡将获得生产商颁发的大奖(好汉卡一套共108张,每张上画有一将,每将都有很多张).
(1)若每完成一笔网络支付交易获赠每种“福”字卡的可能性相同.
①求获得第二种“福”字卡的概率;
②平均要完成多少笔交易才能集齐5个不同的“福”字卡?
(2)如果购买一袋脆干面随赠一张一百单八将的好汉卡中每一张的可能性是一样的,那么平均要购买多少袋脆干面才能获得生产商颁发的大奖?(结果保留到整数)
参考信息:
①.如果在一次试验中某事件发生的概率是p,那么在独立重复试验中,某事件第1次发生时所作试验的次数 的概率分本
的概率分本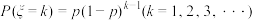 ,称
,称 服从几何分布,记作
服从几何分布,记作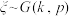 ;
; 的数学期望
的数学期望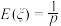 ;
;
②.若干个相互独立、且是按先后次序依次连续发生的随机变量之和的数学期望等于这些随机变量数学期望的之和;
③.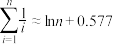 ,
, .
.
(1)若每完成一笔网络支付交易获赠每种“福”字卡的可能性相同.
①求获得第二种“福”字卡的概率;
②平均要完成多少笔交易才能集齐5个不同的“福”字卡?
(2)如果购买一袋脆干面随赠一张一百单八将的好汉卡中每一张的可能性是一样的,那么平均要购买多少袋脆干面才能获得生产商颁发的大奖?(结果保留到整数)
参考信息:
①.如果在一次试验中某事件发生的概率是p,那么在独立重复试验中,某事件第1次发生时所作试验的次数
 的概率分本
的概率分本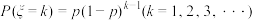 ,称
,称 服从几何分布,记作
服从几何分布,记作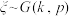 ;
; 的数学期望
的数学期望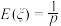 ;
;②.若干个相互独立、且是按先后次序依次连续发生的随机变量之和的数学期望等于这些随机变量数学期望的之和;
③.
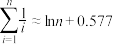 ,
, .
.
您最近一年使用:0次
2021-01-03更新
|
2081次组卷
|
7卷引用:云南省昆明市第一中学2021届高三年级12月月考理科数学试题
云南省昆明市第一中学2021届高三年级12月月考理科数学试题河南省新乡市辉县市一中2020-2021学年高二(培优班)下学期第一次阶段性考试数学理试题(已下线)7.4二项分布和超几何分布C卷(已下线)2023年四省联考变试题17-22(已下线)第四篇 概率与统计 专题7 常见分布 微点3 常见分布综合训练(已下线)第四篇 概率与统计 专题7 常见分布 微点2 其它分布(已下线)第三章 随机变量及其分布列 专题三 重要的概率分布模型 微点4 概率分布模型拓展【培优版】
名校
解题方法
8 . 某冰糖橙是甜橙的一种,以味甜皮薄著称.该橙按照等级可分为四类:珍品、特级、优级和一级.某采购商打算订购一批橙子销往省外,并从采购的这批橙子中随机抽取100箱(每箱有5kg),利用橙子的等级分类标准得到的数据如下表:
(1)若将频率作为概率,从这100箱橙子中有放回地随机抽取4箱,求恰好有2箱是一级品的概率;
(2)利用样本估计总体,果园老板提出两种方案供采购商参考:方案一:不分等级出售,价格为27元/kg;方案二:分等级出售,橙子价格如下表.
从采购商的角度考虑,应该采用哪种方案?
(3)用分层随机抽样的方法从这100箱橙子中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的珍品的箱数,求X的分布列及均值 .
.
| 等级 | 珍品 | 特级 | 优级 | 一级 |
| 箱数 | 40 | 30 | 10 | 20 |
(2)利用样本估计总体,果园老板提出两种方案供采购商参考:方案一:不分等级出售,价格为27元/kg;方案二:分等级出售,橙子价格如下表.
| 等级 | 珍品 | 特级 | 优级 | 一级 |
| 价格/(元∕kg) | 36 | 30 | 24 | 18 |
(3)用分层随机抽样的方法从这100箱橙子中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的珍品的箱数,求X的分布列及均值
 .
.
您最近一年使用:0次
2022-03-14更新
|
507次组卷
|
7卷引用:云南省昆明市师大附中高三上学期(二)数学试题
9 . 为了引导学生阅读世界经典文学名著,某学校举办“名著读书日”活动,每个月选择一天为“名著读书日”,并给出一些推荐书目.为了了解此活动促进学生阅读文学名著的情况,该校在此活动持续进行了一年之后,随机抽取了校内100名学生,调查他们在开始举办读书活动前后的一年时间内的名著阅读数量,所得数据如下表:
(1)依据小概率值 的独立性检验,分析举办该读书活动对学生阅读文学名著是否有促进作用;
的独立性检验,分析举办该读书活动对学生阅读文学名著是否有促进作用;
(2)已知某学生计划在接下来的一年内阅读6本文学名著,其中4本国外名著,2本国内名著,现从6本名著中随机抽取3本在上半年读完,求上半年读完的国内名著本数 的分布列及数学期望.
的分布列及数学期望.
附: ,其中
,其中 .
.
临界值表:
不少于5本 | 少于5本 | 合计 | |
活动前 | 35 | 65 | 100 |
活动后 | 60 | 40 | 100 |
合计 | 95 | 105 | 200 |
 的独立性检验,分析举办该读书活动对学生阅读文学名著是否有促进作用;
的独立性检验,分析举办该读书活动对学生阅读文学名著是否有促进作用;(2)已知某学生计划在接下来的一年内阅读6本文学名著,其中4本国外名著,2本国内名著,现从6本名著中随机抽取3本在上半年读完,求上半年读完的国内名著本数
 的分布列及数学期望.
的分布列及数学期望.附:
 ,其中
,其中 .
.临界值表:
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
10 . 为了研究学生的性别与是否喜欢运动的关联性,随机调查了某中学的50名学生,整理得到如下列联表:
(1)依据 的独立性检验,能否认为学生的性别与是否喜欢运动有关联?
的独立性检验,能否认为学生的性别与是否喜欢运动有关联?
(2)现从喜欢运动的学生中随机抽取3人进行进一步的检测,设随机变量 为男学生的人数,求
为男学生的人数,求 的分布列和数学期望.
的分布列和数学期望.
附:
参考公式: ,其中
,其中 .
.
| 男学生 | 女学生 | 合计 | |
| 喜欢运动 | 8 | 4 | 12 |
| 不喜欢运动 | 2 | 36 | 38 |
| 合计 | 10 | 40 | 50 |
 的独立性检验,能否认为学生的性别与是否喜欢运动有关联?
的独立性检验,能否认为学生的性别与是否喜欢运动有关联?(2)现从喜欢运动的学生中随机抽取3人进行进一步的检测,设随机变量
 为男学生的人数,求
为男学生的人数,求 的分布列和数学期望.
的分布列和数学期望.附:
 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 .
.
您最近一年使用:0次



