名校
1 . 若样本数据 的标准差为6,则数据
的标准差为6,则数据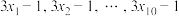 的标准差为( )
的标准差为( )
 的标准差为6,则数据
的标准差为6,则数据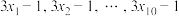 的标准差为( )
的标准差为( )| A.10 | B.14 | C.18 | D.22 |
您最近一年使用:0次
名校
2 . 已知某随机变量 的分布列如图表,则随机变量X的方差
的分布列如图表,则随机变量X的方差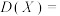 ( )
( )
 的分布列如图表,则随机变量X的方差
的分布列如图表,则随机变量X的方差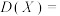 ( )
( ) |  |  |  |
 |  |  |  |
| A.120 | B.160 | C.200 | D.260 |
您最近一年使用:0次
2024-04-10更新
|
1597次组卷
|
5卷引用:陕西省西安市八校联考2023-2024学年高三下学期理科数学试题
陕西省西安市八校联考2023-2024学年高三下学期理科数学试题(已下线)第七章 随机变量及其分布(基础卷)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019选择性必修第三册)(已下线)8.4 离散型随机变量的分布列,期望与方差(高考真题素材之十年高考)重庆市杨家坪中学2023-2024学年高二下学期第二次月考数学试题河北省石家庄十二中2023-2024学年高二下学期期中数学试题
解题方法
3 . 陕西省从2022年秋季启动新高考,新高考“ ”模式中“3”为全国统一高考科目的语文、数学、外语,“1”为首选科目,要求从物理、历史2门科目中确定1门,“2”为再选科目,要求从思想政治、地理、化学、生物学4门科目中确定2门,共计产生12种组合.某班有学生50名,在选科时,首选科目选历史和物理的统计数据如下表所示:
”模式中“3”为全国统一高考科目的语文、数学、外语,“1”为首选科目,要求从物理、历史2门科目中确定1门,“2”为再选科目,要求从思想政治、地理、化学、生物学4门科目中确定2门,共计产生12种组合.某班有学生50名,在选科时,首选科目选历史和物理的统计数据如下表所示:
附: ,其中
,其中 .
.
(1)根据表中的数据,判断是否有 的把握认为学生选择历史与性别有关;
的把握认为学生选择历史与性别有关;
(2)从选择历史的10名学生中任意抽取3名同学参加学校“铭记历史,强国有我”演讲比赛,设 为抽取的三名学生中女生的人数,求
为抽取的三名学生中女生的人数,求 的分布列,并求数学期望和方差.
的分布列,并求数学期望和方差.
 ”模式中“3”为全国统一高考科目的语文、数学、外语,“1”为首选科目,要求从物理、历史2门科目中确定1门,“2”为再选科目,要求从思想政治、地理、化学、生物学4门科目中确定2门,共计产生12种组合.某班有学生50名,在选科时,首选科目选历史和物理的统计数据如下表所示:
”模式中“3”为全国统一高考科目的语文、数学、外语,“1”为首选科目,要求从物理、历史2门科目中确定1门,“2”为再选科目,要求从思想政治、地理、化学、生物学4门科目中确定2门,共计产生12种组合.某班有学生50名,在选科时,首选科目选历史和物理的统计数据如下表所示:| 历史 | 物理 | 合计 | |
| 男生 | 2 | 23 | 25 |
| 女生 | 8 | 17 | 25 |
| 合计 | 10 | 40 | 50 |
 ,其中
,其中 .
. | 0.100 | 0.050 | 0.010 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 的把握认为学生选择历史与性别有关;
的把握认为学生选择历史与性别有关;(2)从选择历史的10名学生中任意抽取3名同学参加学校“铭记历史,强国有我”演讲比赛,设
 为抽取的三名学生中女生的人数,求
为抽取的三名学生中女生的人数,求 的分布列,并求数学期望和方差.
的分布列,并求数学期望和方差.
您最近一年使用:0次
2024-03-24更新
|
455次组卷
|
2卷引用:陕西省咸阳市2024届高三下学期高考模拟检测(二)数学(理科)试题
名校
解题方法
4 . 概率论中有很多经典的不等式,其中最著名的两个当属由两位俄国数学家马尔科夫和切比雪夫分别提出的马尔科夫(Markov)不等式和切比雪夫(Chebyshev)不等式.马尔科夫不等式的形式如下:
设 为一个非负随机变量,其数学期望为
为一个非负随机变量,其数学期望为 ,则对任意
,则对任意 ,均有
,均有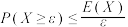 ,
,
马尔科夫不等式给出了随机变量取值不小于某正数的概率上界,阐释了随机变量尾部取值概率与其数学期望间的关系.当 为非负离散型随机变量时,马尔科夫不等式的证明如下:
为非负离散型随机变量时,马尔科夫不等式的证明如下:
设 的分布列为
的分布列为 其中
其中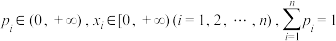 ,则对任意
,则对任意 ,
,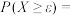
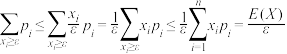 ,其中符号
,其中符号 表示对所有满足
表示对所有满足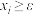 的指标
的指标 所对应的
所对应的 求和.
求和.
切比雪夫不等式的形式如下:
设随机变量 的期望为
的期望为 ,方差为
,方差为 ,则对任意
,则对任意 ,均有
,均有
(1)根据以上参考资料,证明切比雪夫不等式对离散型随机变量 成立.
成立.
(2)某药企研制出一种新药,宣称对治疗某种疾病的有效率为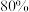 .现随机选择了100名患者,经过使用该药治疗后,治愈的人数为60人,请结合切比雪夫不等式通过计算说明药厂的宣传内容是否真实可信.
.现随机选择了100名患者,经过使用该药治疗后,治愈的人数为60人,请结合切比雪夫不等式通过计算说明药厂的宣传内容是否真实可信.
设
 为一个非负随机变量,其数学期望为
为一个非负随机变量,其数学期望为 ,则对任意
,则对任意 ,均有
,均有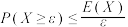 ,
,马尔科夫不等式给出了随机变量取值不小于某正数的概率上界,阐释了随机变量尾部取值概率与其数学期望间的关系.当
 为非负离散型随机变量时,马尔科夫不等式的证明如下:
为非负离散型随机变量时,马尔科夫不等式的证明如下:设
 的分布列为
的分布列为 其中
其中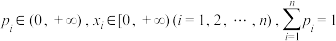 ,则对任意
,则对任意 ,
,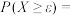
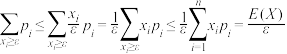 ,其中符号
,其中符号 表示对所有满足
表示对所有满足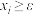 的指标
的指标 所对应的
所对应的 求和.
求和.切比雪夫不等式的形式如下:
设随机变量
 的期望为
的期望为 ,方差为
,方差为 ,则对任意
,则对任意 ,均有
,均有
(1)根据以上参考资料,证明切比雪夫不等式对离散型随机变量
 成立.
成立.(2)某药企研制出一种新药,宣称对治疗某种疾病的有效率为
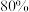 .现随机选择了100名患者,经过使用该药治疗后,治愈的人数为60人,请结合切比雪夫不等式通过计算说明药厂的宣传内容是否真实可信.
.现随机选择了100名患者,经过使用该药治疗后,治愈的人数为60人,请结合切比雪夫不等式通过计算说明药厂的宣传内容是否真实可信.
您最近一年使用:0次
2023-05-27更新
|
3353次组卷
|
13卷引用:陕西省铜川市2024届高三一模数学(理)试题
陕西省铜川市2024届高三一模数学(理)试题吉林省东北师范大学附中2023届高三下学期七模数学试题吉林省长春市东北师范大学附属中学2023届高三第七次模拟考试数学试题(已下线)第07讲 离散型随机变量的分布列与数字特征(六大题型)(讲义)广东省佛山市2024届高三上学期教育教学质量检测模拟(一)数学试题(已下线)随机变量及其分布专题15离散型随机变量的分布列(已下线)专题22 新高考新题型第19题新定义压轴解答题归纳(9大题型)(练习)(已下线)专题6 概率与统计中的新定义压轴大题(过关集训)(已下线)第四篇 概率与统计 专题4 分赌注问题 微点1 分赌注问题(已下线)高三开学收心考试模拟卷(已下线)重难点突破01 概率与统计的综合应用(十八大题型)-2(已下线)重难点突破03 高等背景下概率论新定义(七大题型)
名校
5 . 已知离散型随机变量 的取值为0,1,2,且
的取值为0,1,2,且 ,
, ,
,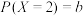 ;若
;若 ,则
,则
___________ .
 的取值为0,1,2,且
的取值为0,1,2,且 ,
, ,
,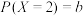 ;若
;若 ,则
,则
您最近一年使用:0次
2020-10-20更新
|
586次组卷
|
8卷引用:陕西省渭南市瑞泉中学2024届高三第六次质量检测数学(理科)试题
陕西省渭南市瑞泉中学2024届高三第六次质量检测数学(理科)试题广东省东莞市2017-2018学年高二(下)期末数学(理科)试题(已下线)4.2.4随机变量的数字特征(2)A基础练(已下线)专题4.6《随机变量》单元测试卷(B卷提升篇)-2020-2021学年高二数学选择性必修第二册同步单元AB卷(新教材人教B版)(已下线)专题15 随机变量的分布列与期望 -备战2021年新高考数学纠错笔记 (已下线)【新教材精创】7.3.2离散型随机变量的方差 -A基础练沪教版(2020) 选修第二册 堂堂清 第7章 单元复习七黑龙江省齐齐哈尔市恒昌中学校2022-2023学年高二下学期期中数学试题



