名校
解题方法
1 . 法国数学家庞加莱是个喜欢吃面包的人,他每天都会到同一家面包店购买一个面包.该面包店的面包师声称自己所出售的面包的平均质量是1 000 g,上下浮动不超过50 g.这句话用数学语言来表达就是:每个面包的质量服从期望为1 000 g,标准差为50 g的正态分布.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N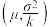 .利用该结论解决下面问题.
.利用该结论解决下面问题.
①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
(1)已知如下结论:若X~N(μ,σ2),从X的取值中随机抽取k(k∈N*,k≥2)个数据,记这k个数据的平均值为Y,则随机变量Y~N
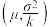 .利用该结论解决下面问题.
.利用该结论解决下面问题.①假设面包师的说法是真实的,随机购买25个面包,记随机购买25个面包的平均值为Y,求P(Y≤980);
②庞加莱每天都会将买来的面包称重并记录,25天后,得到的数据都落在区间(950,1 050)内,并得出计算25个面包的平均质量为978.72 g.庞加莱通过分析举报了该面包师,从概率角度说明庞加莱举报该面包师的理由;
(2)假设有两箱面包(面包除颜色外,其他都一样),已知第一箱中共装有6个面包,其中黑色面包2个;第二箱中共装有8个面包,其中黑色面包3个.现随机挑选一箱,然后从该箱中随机取出2个面包,求取出黑色面包个数的分布列及数学期望.
附:①若随机变量η服从正态分布N(μ,σ2),则P(μ-σ≤η≤μ+σ)≈0.682 7,P(μ-2σ≤η≤μ+2σ)≈0.954 5,P(μ-3σ≤η≤μ+3σ)≈0.997 3;②通常把发生概率小于0.05的事件称为小概率事件,小概率事件基本不会发生.
您最近一年使用:0次
2024-03-21更新
|
500次组卷
|
21卷引用:辽宁省锦州市某校2023-2024学年高三上学期第二次考试数学试题
辽宁省锦州市某校2023-2024学年高三上学期第二次考试数学试题山东省青岛市四区2021-2022学年高三上学期期末考试数学试题福建省尤溪第一中学2021~2022学年高二下学期数学期末模拟卷(三)试题湖南省长沙市雅礼中学2022-2023学年高三上学期月考(五)数学试题山东省青岛市4区县2021-2022学年高三上学期期末考试数学试题浙江省杭州第二中学2023届高三下学期3月月考数学试题江苏省常州市溧阳中学2022-2023学年高二下学期4月阶段性调研测试数学试题江苏省扬州中学2023届高三下学期阶段测试数学试题河北省保定市六校联盟2022-2023学年高二下学期4月联考数学试题江苏省盐城市伍佑中学2023届高三高考热身考试数学试题(已下线)8.3 正态分布辽宁省大连市第八中学2023届高考适应性测试数学试题福建省厦门第一中学2023届高三二模数学试题(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-3(已下线)专题04 超几何分布+二项分布+正态分布压轴题(3)(已下线)第八章 概率(单元重点综合测试)-2023-2024学年高二数学单元速记·巧练(苏教版2019选择性必修第二册)(已下线)8.3 正态分布(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第8章 概率单元综合能力测试卷-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第七章:随机变量及其分布章末重点题型复习-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)黑龙江省牡丹江市第一高级中学2023-2024学年高二下学期5月期中考试数学试题(已下线)专题06 离散型随机变量与正态分布--高二期末考点大串讲(苏教版2019选择性必修第二册)



