有 、
、 两种型号的货车,用
两种型号的货车,用 辆
辆 型货车和
型货车和 辆
辆 型货车装满货物一次可运货
型货车装满货物一次可运货 吨;用
吨;用 辆
辆 型货车和
型货车和 辆
辆 型货车装满货物一次可运货
型货车装满货物一次可运货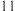 吨.请用学过的方程(组)知识解答下列问题:
吨.请用学过的方程(组)知识解答下列问题:
(1)求 型、
型、 型两种货车装满货物每辆分别能运货多少吨?
型两种货车装满货物每辆分别能运货多少吨?
(2)某物流公司有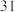 吨货物,计划同时租用
吨货物,计划同时租用 型车
型车 辆,
辆, 型车
型车 辆,一次运完,且恰好每辆车都装满货物.若
辆,一次运完,且恰好每辆车都装满货物.若 型货车每辆需租金
型货车每辆需租金 元/次,
元/次, 型货车每辆需租金
型货车每辆需租金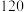 元/次.请直接写出该物流公司所有租车方案,并求出最少租车费用.
元/次.请直接写出该物流公司所有租车方案,并求出最少租车费用.
 、
、 两种型号的货车,用
两种型号的货车,用 辆
辆 型货车和
型货车和 辆
辆 型货车装满货物一次可运货
型货车装满货物一次可运货 吨;用
吨;用 辆
辆 型货车和
型货车和 辆
辆 型货车装满货物一次可运货
型货车装满货物一次可运货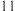 吨.请用学过的方程(组)知识解答下列问题:
吨.请用学过的方程(组)知识解答下列问题:(1)求
 型、
型、 型两种货车装满货物每辆分别能运货多少吨?
型两种货车装满货物每辆分别能运货多少吨?(2)某物流公司有
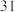 吨货物,计划同时租用
吨货物,计划同时租用 型车
型车 辆,
辆, 型车
型车 辆,一次运完,且恰好每辆车都装满货物.若
辆,一次运完,且恰好每辆车都装满货物.若 型货车每辆需租金
型货车每辆需租金 元/次,
元/次, 型货车每辆需租金
型货车每辆需租金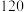 元/次.请直接写出该物流公司所有租车方案,并求出最少租车费用.
元/次.请直接写出该物流公司所有租车方案,并求出最少租车费用.
20-21七年级下·安徽芜湖·阶段练习 查看更多[7]
安徽省芜湖市无为市2020-2021学年七年级下学期第三次月考数学试题福建省福州市罗源县罗源第一中学2021-2022学年七年级下学期期中数学试题(已下线)专题5.1 二元一次方程组的应用题 十一大考点专项讲练-2022-2023学年八年级数学上册重难题型全归纳及技巧提升专项精练(北师大版)(已下线)专题5.2 二元一次方程组的应用题-【帮课堂】2022-2023学年八年级数学上册同步精品讲义(北师大版)(已下线)第19章 一次函数(A卷·知识通关练)-【单元测试】2022-2023学年八年级数学下册分层训练AB卷(人教版)陕西西安雁塔区西安电子科技大学附属中学2022-2023学年八年级上学期期中数学试题(已下线)专题6.20 用一次函数解决问题(分层练习)(提升练)-2023-2024学年八年级数学上册基础知识专项突破讲与练(苏科版)
更新时间:2023/09/29 22:25:51
|
相似题推荐
解答题-应用题
|
适中
(0.65)
【推荐1】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和1部乙型号手机,共需要资金8400元;若购进3部甲型号手机和2部乙型号手机,共需要资金13800元.
(1)求甲、乙型号手机每部进价各为多少元?
(2)该店计划购进甲乙两种型号的手机销售,预计用不多于5.52万元且不少于5.28万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)若甲型号手机的售价为4500元,乙型号手机的售价为4200元,为了促销,无论采取哪种进货方案,公司决定每售出一台乙型号手机,返还顾客相同现金a元,而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
(1)求甲、乙型号手机每部进价各为多少元?
(2)该店计划购进甲乙两种型号的手机销售,预计用不多于5.52万元且不少于5.28万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)若甲型号手机的售价为4500元,乙型号手机的售价为4200元,为了促销,无论采取哪种进货方案,公司决定每售出一台乙型号手机,返还顾客相同现金a元,而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐2】为了预防新冠肺炎,某药店销售甲、乙两种防护口罩,已知甲种口罩每袋的售价比乙种口罩多 元,小明从该药店购买了
元,小明从该药店购买了 袋甲口罩和
袋甲口罩和 袋乙口罩共花费
袋乙口罩共花费 元.
元.
(1)求该药店甲、乙两种口罩每袋的售价分别为多少元.
(2)根据消费者需求,该药店决定用不超过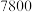 元购进甲、乙两种口罩共
元购进甲、乙两种口罩共 袋,已知甲种口罩每袋的进价为
袋,已知甲种口罩每袋的进价为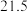 元,乙种口罩每袋的进价为
元,乙种口罩每袋的进价为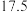 元.若所购进口罩均可全部售出,请求出该药店所获利润
元.若所购进口罩均可全部售出,请求出该药店所获利润 (元)与甲种口罩的进货量
(元)与甲种口罩的进货量 (袋)之间的函数关系式.
(袋)之间的函数关系式.
(3)在(2)的前提下,要使药店获利最大,应该购进甲、乙两种口罩各多少袋,并求出最大利润.
 元,小明从该药店购买了
元,小明从该药店购买了 袋甲口罩和
袋甲口罩和 袋乙口罩共花费
袋乙口罩共花费 元.
元.(1)求该药店甲、乙两种口罩每袋的售价分别为多少元.
(2)根据消费者需求,该药店决定用不超过
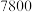 元购进甲、乙两种口罩共
元购进甲、乙两种口罩共 袋,已知甲种口罩每袋的进价为
袋,已知甲种口罩每袋的进价为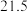 元,乙种口罩每袋的进价为
元,乙种口罩每袋的进价为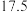 元.若所购进口罩均可全部售出,请求出该药店所获利润
元.若所购进口罩均可全部售出,请求出该药店所获利润 (元)与甲种口罩的进货量
(元)与甲种口罩的进货量 (袋)之间的函数关系式.
(袋)之间的函数关系式.(3)在(2)的前提下,要使药店获利最大,应该购进甲、乙两种口罩各多少袋,并求出最大利润.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
【推荐1】A市有某种型号的农用车50辆,B市有40辆,现要将这些农用车全部调往C、D两县,C县需要该种农用车42辆,D县需要48辆,从A市运往C、D两县农用车的费用分别为每辆300元和150元,从B市运往C、D两县农用车的费用分别为每辆200元和250元.
(1)设从A市运往C县的农用车为x辆,此次调运总费为y元,求y与x的函数关系式,并写出自变量x的取值范围;
(2)若此次调运的总费用不超过16000元,有哪几种调运方案?哪种方案的费用最小?并求出最小费用?
(1)设从A市运往C县的农用车为x辆,此次调运总费为y元,求y与x的函数关系式,并写出自变量x的取值范围;
(2)若此次调运的总费用不超过16000元,有哪几种调运方案?哪种方案的费用最小?并求出最小费用?
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
名校
【推荐2】为了帮助湖北省武汉市防控新冠肺炎,某爱心组织筹集了部分资金,计划购买甲、乙两种救灾物资共2000件送往灾区,已知每件甲种物资的价格比每件乙种物资的价格贵10元,用350元购买甲种物资的件数恰好与用300元购买乙种物资的件数相同.
(1)求甲、乙两种救灾物资每件的价格各是多少元?
(2)经调查,灾区对甲种物资的需求量不少于乙种物资的1.5倍,若该爱心组织如何购买这2000件物资,才能使得购买资金最少?
(1)求甲、乙两种救灾物资每件的价格各是多少元?
(2)经调查,灾区对甲种物资的需求量不少于乙种物资的1.5倍,若该爱心组织如何购买这2000件物资,才能使得购买资金最少?
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐3】某公司在甲、乙两个生产基地分别生产了同一种型号的检测设备15台、17台,现要把这些设备全部运往 、
、 两市.
两市. 市需要19台,
市需要19台, 市需要13台.且运往
市需要13台.且运往 、
、 两市的运费如下表:
两市的运费如下表:
设从甲基地运往 市的设备为
市的设备为 台,从甲基地运往两市的总运费为
台,从甲基地运往两市的总运费为 元,从乙基地运往两市的总运费为
元,从乙基地运往两市的总运费为 元.
元.
(1)分别写出 、
、 与
与 之间的函数关系式(不要求写自变量的取值范围);
之间的函数关系式(不要求写自变量的取值范围);
(2)试比较甲、乙两基地总运费的大小;
(3)若乙基地的总运费不得超过11300元,怎样调运,使两基地总运费的和最小?并求出最小值.
 、
、 两市.
两市. 市需要19台,
市需要19台, 市需要13台.且运往
市需要13台.且运往 、
、 两市的运费如下表:
两市的运费如下表:| 两市 两基地 |  市(元/台) 市(元/台) |  市(元/台) 市(元/台) |
| 甲 | 500 | 800 |
| 乙 | 600 | 700 |
 市的设备为
市的设备为 台,从甲基地运往两市的总运费为
台,从甲基地运往两市的总运费为 元,从乙基地运往两市的总运费为
元,从乙基地运往两市的总运费为 元.
元.(1)分别写出
 、
、 与
与 之间的函数关系式(不要求写自变量的取值范围);
之间的函数关系式(不要求写自变量的取值范围);(2)试比较甲、乙两基地总运费的大小;
(3)若乙基地的总运费不得超过11300元,怎样调运,使两基地总运费的和最小?并求出最小值.
您最近一年使用:0次



