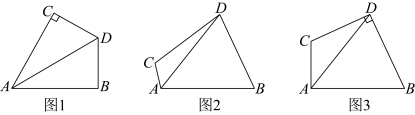
在四边形 中,
中, 平分
平分 ,并且
,并且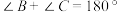 .
. 时,则
时,则 与
与 的数量关系是______;
的数量关系是______;
(2)如图2,当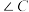 是钝角时,(1)中的结论是否仍然成立?请证明你的判断;
是钝角时,(1)中的结论是否仍然成立?请证明你的判断;
(3)如图3,若 ,
,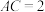 ,
, ,求
,求 的面积
的面积
 中,
中, 平分
平分 ,并且
,并且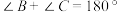 .
.
 时,则
时,则 与
与 的数量关系是______;
的数量关系是______;(2)如图2,当
 是钝角时,(1)中的结论是否仍然成立?请证明你的判断;
是钝角时,(1)中的结论是否仍然成立?请证明你的判断;(3)如图3,若
 ,
, ,
, ,求
,求 的面积
的面积
更新时间:2024/04/24 13:17:04
|
相似题推荐
解答题-证明题
|
适中
(0.65)
【推荐1】如图,在矩形ABCD中,AD=kAB(k>0),点E是线段CB延长线上的一个动点,连接AE,过点A作AF⊥AE交射线DC于点F.
(1)如图1,若k=1,则AF与AE之间的数量关系是 ;
(2)如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)
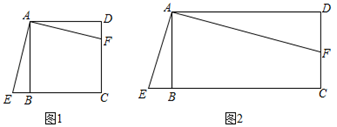
(1)如图1,若k=1,则AF与AE之间的数量关系是 ;
(2)如图2,若k≠1,试判断AF与AE之间的数量关系,写出结论并证明;(用含k的式子表示)

您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐2】已知抛物线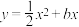 与直线
与直线 交于点
交于点 、
、
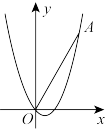
(1)求抛物线的解析式;
(2)将射线 绕原点逆时针旋转
绕原点逆时针旋转 后与抛物线交于点P,求P点的坐标.
后与抛物线交于点P,求P点的坐标.
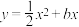 与直线
与直线 交于点
交于点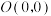 、
、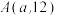

(1)求抛物线的解析式;
(2)将射线
 绕原点逆时针旋转
绕原点逆时针旋转 后与抛物线交于点P,求P点的坐标.
后与抛物线交于点P,求P点的坐标.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
名校
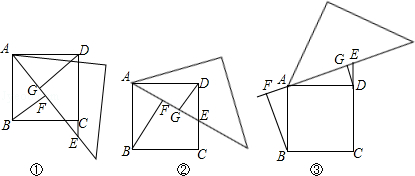
【推荐1】问题情境:在数学活动课上,老师出示了这样一个问题:如图①, 中,
中, 平分
平分 ,
, 垂直平分
垂直平分 .试判断
.试判断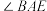 与
与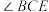 的数量关系;
的数量关系;
探究展示:智慧小组发现,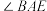 与
与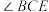 互为补角,并展示了如下的证明方法:
互为补角,并展示了如下的证明方法:
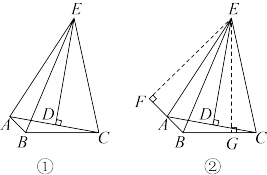
证明:如图②,作 交
交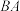 的延长线于点F,
的延长线于点F, 于点G,
于点G,
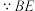 平分
平分 ,
,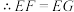 ,(依据1)
,(依据1)
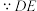 垂直平分
垂直平分 ,
, ,(依据2)
,(依据2)
……
反思交流:
(1)上述证明过程中的“依据1”“依据2”分别是指什么?
(2)请按照上面的证明思路,完整写出该题证明过程.
 中,
中, 平分
平分 ,
, 垂直平分
垂直平分 .试判断
.试判断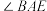 与
与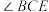 的数量关系;
的数量关系;探究展示:智慧小组发现,
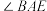 与
与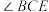 互为补角,并展示了如下的证明方法:
互为补角,并展示了如下的证明方法:证明:如图②,作
 交
交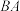 的延长线于点F,
的延长线于点F, 于点G,
于点G,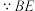 平分
平分 ,
,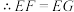 ,(依据1)
,(依据1)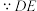 垂直平分
垂直平分 ,
, ,(依据2)
,(依据2)……

反思交流:
(1)上述证明过程中的“依据1”“依据2”分别是指什么?
(2)请按照上面的证明思路,完整写出该题证明过程.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐2】如图,P为 平分线上一点,
平分线上一点, 于A,
于A, 于B.
于B. ;
;
(2)求证: 垂直平分
垂直平分 .
.
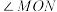 平分线上一点,
平分线上一点, 于A,
于A, 于B.
于B.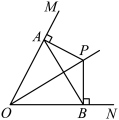
 ;
;(2)求证:
 垂直平分
垂直平分 .
.
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
【推荐1】如图,点D是△ABC的边BC上的中点,F,E分别是线段AD及其延长线上的点,CF∥BE,连结BF,CE.
(1)求证:四边形BECF是平行四边形;
(2)若AB=13,则AC的长为多少时,四边形BECF是菱形,请说明理由;
(3)若AB=13,BC=10且四边形BECF是正方形,则直接写出AF的长为 .
(1)求证:四边形BECF是平行四边形;
(2)若AB=13,则AC的长为多少时,四边形BECF是菱形,请说明理由;
(3)若AB=13,BC=10且四边形BECF是正方形,则直接写出AF的长为 .

您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
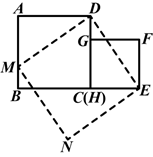
【推荐2】如图所示,已知正方形ABCD,直角三角形纸板的一个锐角顶点与点A重合,纸板绕点A旋转时,直角三角形纸板的一边与直线CD交于E,分别过B、D作直线AE的垂线,垂足分别为F、G.
(1)当点E在DC延长线时,如图①,求证:BF=DG﹣FG;
(2)将图①中的三角板绕点A逆时针旋转得图②、图③,此时BF、FG、DG之间又有怎样的数量关系?请直接写出结论(不必证明)

(1)当点E在DC延长线时,如图①,求证:BF=DG﹣FG;
(2)将图①中的三角板绕点A逆时针旋转得图②、图③,此时BF、FG、DG之间又有怎样的数量关系?请直接写出结论(不必证明)
您最近一年使用:0次
解答题-证明题
|
适中
(0.65)
解题方法
【推荐3】操作示例
对于边长为a的两个正方形ABCD和EFGH,按图1所示的方式摆放,沿虚线BD、EG剪开后,可以按图1所示的移动方式拼接为四边形BNED.从拼接的过程容易得到结论:

①四边形BNED是正方形;
②S正方形ABCD+S正方形EFGH=S正方形BNED.
实践与探究
(1)对于边长分别为a,b(a>b)的两个正方形ABCD和EFGH,按图2所示的方式摆放,连接DE,过点D作DM⊥DE,交AB于点M,过点M作MN⊥DM,过点E作EN⊥DE,MN与EN相交于点N.
①证明:四边形MNED是正方形,并用含a,b的代数式表示正方形MNED的面积;
②在图2中,将正方形ABCD和正方形EFGH沿虚线剪开后,能够拼接为正方形MNED,请简略说明你的拼接方法(类比图1,用数字表示对应的图形);
(2)对于n(n是大于2的自然数)个任意的正方形,能否通过若干次拼接,将其拼接成为一个正方形?请简要说明你的理由.
对于边长为a的两个正方形ABCD和EFGH,按图1所示的方式摆放,沿虚线BD、EG剪开后,可以按图1所示的移动方式拼接为四边形BNED.从拼接的过程容易得到结论:

①四边形BNED是正方形;
②S正方形ABCD+S正方形EFGH=S正方形BNED.
实践与探究
(1)对于边长分别为a,b(a>b)的两个正方形ABCD和EFGH,按图2所示的方式摆放,连接DE,过点D作DM⊥DE,交AB于点M,过点M作MN⊥DM,过点E作EN⊥DE,MN与EN相交于点N.
①证明:四边形MNED是正方形,并用含a,b的代数式表示正方形MNED的面积;
②在图2中,将正方形ABCD和正方形EFGH沿虚线剪开后,能够拼接为正方形MNED,请简略说明你的拼接方法(类比图1,用数字表示对应的图形);

(2)对于n(n是大于2的自然数)个任意的正方形,能否通过若干次拼接,将其拼接成为一个正方形?请简要说明你的理由.
您最近一年使用:0次

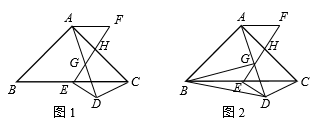
 中,
中, ,
,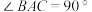 ,
, 为
为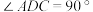 ,
, 为
为 中点,
中点,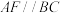 ,连接
,连接 交
交 ,且
,且 交
交 ,
, .
.
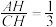 ,求
,求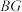 ,若
,若 ,求证:
,求证: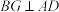 .
.

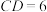
 .
.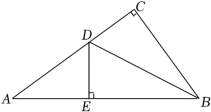
 的长;
的长;

