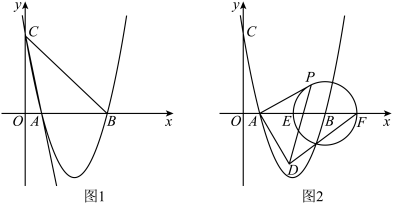
如图1,在平面直角坐标系中,直线 与
与 轴,
轴, 轴分别交于
轴分别交于 、
、 两点,抛物线
两点,抛物线 经过
经过 两点,与
两点,与 轴的另一交点为
轴的另一交点为 .
.
(1)求抛物线解析式;
(2)若点 为
为 轴下方抛物线上一动点,当点
轴下方抛物线上一动点,当点 运动到某一位置时,
运动到某一位置时, 的面积等于
的面积等于 面积的
面积的 .求此时点
.求此时点 的坐标;
的坐标;
(3)如图2,以 为圆心,2为半径的
为圆心,2为半径的 与
与 轴交于
轴交于 、
、 两点(
两点( 在
在 右侧),若
右侧),若 点是
点是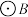 上一动点,连接
上一动点,连接 ,以
,以 为腰作等腰
为腰作等腰 ,使
,使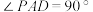 (
( 、
、 、
、 三点为逆时针顺序),连接
三点为逆时针顺序),连接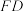 ,求
,求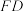 长度的取值范围.
长度的取值范围.
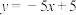 与
与 轴,
轴, 轴分别交于
轴分别交于 、
、 两点,抛物线
两点,抛物线 经过
经过 两点,与
两点,与 轴的另一交点为
轴的另一交点为 .
.
(1)求抛物线解析式;
(2)若点
 为
为 轴下方抛物线上一动点,当点
轴下方抛物线上一动点,当点 运动到某一位置时,
运动到某一位置时, 的面积等于
的面积等于 面积的
面积的 .求此时点
.求此时点 的坐标;
的坐标;(3)如图2,以
 为圆心,2为半径的
为圆心,2为半径的 与
与 轴交于
轴交于 、
、 两点(
两点( 在
在 右侧),若
右侧),若 点是
点是 上一动点,连接
上一动点,连接 ,以
,以 为腰作等腰
为腰作等腰 ,使
,使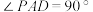 (
( 、
、 、
、 三点为逆时针顺序),连接
三点为逆时针顺序),连接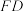 ,求
,求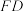 长度的取值范围.
长度的取值范围.
更新时间:2023/09/05 16:57:52
|
相似题推荐
解答题-问答题
|
较难
(0.4)
【推荐1】对任意一个三位自然数n,若各个数位上的数字均不为0,则称该自然数为“无零数”.将这个三位“无零数”的各数位上的数字两两组合,形成六个新的两位数,我们将这六个两位数的和,叫做该三位“无零数”的“二位总和”,将所得的“二位总和”除以44,得到的结果记为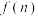 .例如“352”是一个三位“无零数”,六个新数为35,32,53,52,23,25,则
.例如“352”是一个三位“无零数”,六个新数为35,32,53,52,23,25,则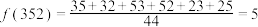 .
.
(1)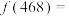 ________,证明:任意一个满足十位数字等于百位数字与个位数字之和的
________,证明:任意一个满足十位数字等于百位数字与个位数字之和的 的三位“无零数”,它的“二位总和”定能被33整除;
的三位“无零数”,它的“二位总和”定能被33整除;
(2)若一个“无零数”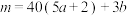 (其中
(其中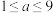 ,
, ,且a,b为整数)的十位数字为8,且满足十位数字等于百位数字与个位数字之和,求
,且a,b为整数)的十位数字为8,且满足十位数字等于百位数字与个位数字之和,求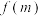 .
.
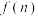 .例如“352”是一个三位“无零数”,六个新数为35,32,53,52,23,25,则
.例如“352”是一个三位“无零数”,六个新数为35,32,53,52,23,25,则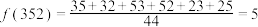 .
.(1)
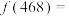 ________,证明:任意一个满足十位数字等于百位数字与个位数字之和的
________,证明:任意一个满足十位数字等于百位数字与个位数字之和的 的三位“无零数”,它的“二位总和”定能被33整除;
的三位“无零数”,它的“二位总和”定能被33整除;(2)若一个“无零数”
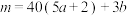 (其中
(其中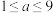 ,
, ,且a,b为整数)的十位数字为8,且满足十位数字等于百位数字与个位数字之和,求
,且a,b为整数)的十位数字为8,且满足十位数字等于百位数字与个位数字之和,求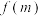 .
.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐2】已知:在平面直角坐标系中,点O为坐标原点,直线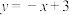 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线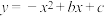 经过
经过 两点,与x轴的另一交点为点A.
两点,与x轴的另一交点为点A.
(2)如图2,点D为直线 上方抛物线上一动点,连接
上方抛物线上一动点,连接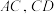 ,设直线
,设直线 交线段
交线段 于点E,
于点E, 的面积为
的面积为 的面积为
的面积为 ,当
,当 最大值时,求点D的坐标;
最大值时,求点D的坐标;
(3)如图3,在(2)的条件下,连接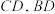 ,将
,将 沿
沿 翻折,得到
翻折,得到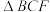 (点D和点F为对应点),直线
(点D和点F为对应点),直线 交y轴于点P,点S为
交y轴于点P,点S为 中点,连接
中点,连接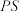 ,过点S作
,过点S作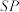 的垂线交x轴于点R,在对称轴
的垂线交x轴于点R,在对称轴 上有一点Q,使得
上有一点Q,使得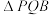 是以
是以 为直角边的直角三角形,求直线
为直角边的直角三角形,求直线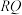 的解析式.
的解析式.
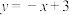 与x轴交于点B,与y轴交于点C,抛物线
与x轴交于点B,与y轴交于点C,抛物线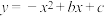 经过
经过 两点,与x轴的另一交点为点A.
两点,与x轴的另一交点为点A.
(2)如图2,点D为直线
 上方抛物线上一动点,连接
上方抛物线上一动点,连接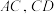 ,设直线
,设直线 交线段
交线段 于点E,
于点E, 的面积为
的面积为 的面积为
的面积为 ,当
,当 最大值时,求点D的坐标;
最大值时,求点D的坐标;(3)如图3,在(2)的条件下,连接
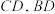 ,将
,将 沿
沿 翻折,得到
翻折,得到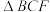 (点D和点F为对应点),直线
(点D和点F为对应点),直线 交y轴于点P,点S为
交y轴于点P,点S为 中点,连接
中点,连接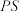 ,过点S作
,过点S作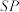 的垂线交x轴于点R,在对称轴
的垂线交x轴于点R,在对称轴 上有一点Q,使得
上有一点Q,使得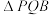 是以
是以 为直角边的直角三角形,求直线
为直角边的直角三角形,求直线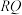 的解析式.
的解析式.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
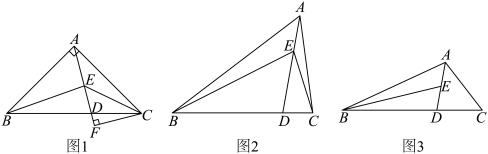
【推荐1】在 中,
中, ,
,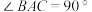 ,点
,点 为平面内一点,
为平面内一点,

(1)如图1,当点 在
在 边上,且
边上,且 时,求
时,求 的长度
的长度
(2)如图2,若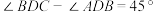 ,求证:
,求证: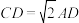
(3)如图3,当 时,连接
时,连接 ,将
,将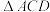 沿直线
沿直线 翻折至
翻折至 平面内得到
平面内得到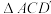 ,点
,点 、
、 分别为
分别为 、
、 中点,
中点, 为线段
为线段 上一动点,连接
上一动点,连接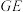 ,将线段
,将线段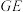 绕点
绕点 顺时针方向旋转90°,得到
顺时针方向旋转90°,得到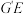 ,请直接写出
,请直接写出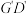 的最小值.
的最小值.
 中,
中, ,
,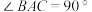 ,点
,点 为平面内一点,
为平面内一点,
(1)如图1,当点
 在
在 边上,且
边上,且 时,求
时,求 的长度
的长度(2)如图2,若
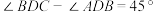 ,求证:
,求证: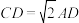
(3)如图3,当
 时,连接
时,连接 ,将
,将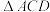 沿直线
沿直线 翻折至
翻折至 平面内得到
平面内得到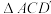 ,点
,点 、
、 分别为
分别为 、
、 中点,
中点, 为线段
为线段 上一动点,连接
上一动点,连接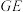 ,将线段
,将线段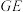 绕点
绕点 顺时针方向旋转90°,得到
顺时针方向旋转90°,得到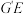 ,请直接写出
,请直接写出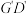 的最小值.
的最小值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐2】如图,在矩形ABCD中,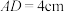 ,
,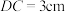 ,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿
,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿 运动.到点B停止,点Q沿
运动.到点B停止,点Q沿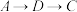 运动,到点C停止. 连接
运动,到点C停止. 连接 ,设
,设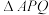 的面积为
的面积为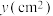 (这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).
(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s). 时,求x的值;
时,求x的值;
(2)当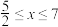 时,求y与x之间的函数关系式;
时,求y与x之间的函数关系式;
(3)直接写出在整个运动过程中,使 的所有
的所有 的值.
的值.
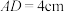 ,
,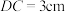 ,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿
,对角线AC、BD相交于点O,动点P、Q分别从点C、A同时出发,运动速度均为1cm/s,点P沿 运动.到点B停止,点Q沿
运动.到点B停止,点Q沿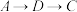 运动,到点C停止. 连接
运动,到点C停止. 连接 ,设
,设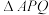 的面积为
的面积为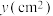 (这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).
(这里规定:线段是面积为0的几何图形),点Q的运动时间为x(s).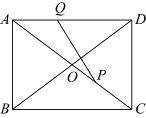
 时,求x的值;
时,求x的值;(2)当
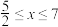 时,求y与x之间的函数关系式;
时,求y与x之间的函数关系式;(3)直接写出在整个运动过程中,使
 的所有
的所有 的值.
的值.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
名校
【推荐3】如图,在正方形ABCD中, .求证:
.求证: .
.
证明:设CE与DF交于点O,
∵四边形ABCD是正方形,
∴ ,
, .
.
∴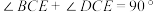 .
.
∵ ,∴
,∴ .
.
∴ .∴
.∴ .
.
∴ .∴
.∴ .
.
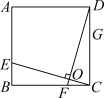
某数学兴趣小组在完成了以上解答后,决定对该问题进一步探究
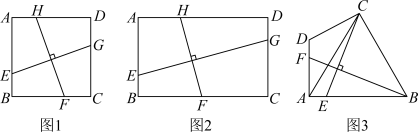
(1)【问题探究】如图1,在正方形ABCD中,点E、F、G、H分别在线段AB、BC、CD、DA上,且 .试猜想
.试猜想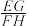 的值,并证明你的猜想.
的值,并证明你的猜想.
(2)【知识迁移】如图2,在矩形ABCD中,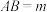 ,
, ,点E、F、G、H分别在线段AB、BC、CD、DA上,且
,点E、F、G、H分别在线段AB、BC、CD、DA上,且 .则
.则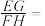 ___________.
___________.
(3)【拓展应用】如图3,在四边形ABCD中, ,
, ,
, ,点E、F分别在线段AB、AD上,且
,点E、F分别在线段AB、AD上,且 .求
.求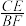 的值.
的值.
 .求证:
.求证: .
.证明:设CE与DF交于点O,
∵四边形ABCD是正方形,
∴
 ,
, .
.∴
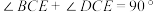 .
.∵
 ,∴
,∴ .
.∴
 .∴
.∴ .
.∴
 .∴
.∴ .
.
某数学兴趣小组在完成了以上解答后,决定对该问题进一步探究

(1)【问题探究】如图1,在正方形ABCD中,点E、F、G、H分别在线段AB、BC、CD、DA上,且
 .试猜想
.试猜想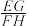 的值,并证明你的猜想.
的值,并证明你的猜想.(2)【知识迁移】如图2,在矩形ABCD中,
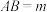 ,
, ,点E、F、G、H分别在线段AB、BC、CD、DA上,且
,点E、F、G、H分别在线段AB、BC、CD、DA上,且 .则
.则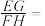 ___________.
___________.(3)【拓展应用】如图3,在四边形ABCD中,
 ,
, ,
, ,点E、F分别在线段AB、AD上,且
,点E、F分别在线段AB、AD上,且 .求
.求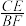 的值.
的值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
【推荐1】如图所示,已知抛物线 与
与 轴交于
轴交于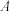 、
、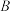 两点,与
两点,与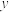 轴交于点
轴交于点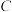 .
.
(1)求 、
、 、
、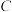 三点的坐标.
三点的坐标.
(2)过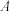 作
作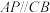 交抛物线于点
交抛物线于点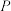 ,求四边形
,求四边形 的面积.
的面积.
(3)在 轴上方的抛物线上是否存在一点
轴上方的抛物线上是否存在一点 ,过
,过 作
作 轴点
轴点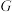 ,使以
,使以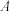 、
、 、
、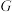 三点为顶点的三角形与
三点为顶点的三角形与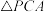 相似.若存在,请求出
相似.若存在,请求出 点的坐标;否则,请说明理由.
点的坐标;否则,请说明理由.
 与
与 轴交于
轴交于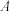 、
、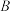 两点,与
两点,与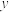 轴交于点
轴交于点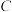 .
.
(1)求
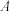 、
、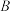 、
、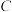 三点的坐标.
三点的坐标.(2)过
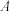 作
作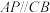 交抛物线于点
交抛物线于点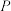 ,求四边形
,求四边形 的面积.
的面积.(3)在
 轴上方的抛物线上是否存在一点
轴上方的抛物线上是否存在一点 ,过
,过 作
作 轴点
轴点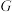 ,使以
,使以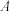 、
、 、
、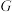 三点为顶点的三角形与
三点为顶点的三角形与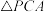 相似.若存在,请求出
相似.若存在,请求出 点的坐标;否则,请说明理由.
点的坐标;否则,请说明理由.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
【推荐2】在平面直角坐标系 中,拋物线
中,拋物线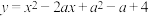 的顶点为
的顶点为 ,点
,点 为直线
为直线 上的两个动点(点
上的两个动点(点 在点
在点 的左侧),且
的左侧),且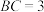 .
.
(1)求点 的坐标(用含
的坐标(用含 的代数式表示);
的代数式表示);
(2)若 是以
是以 为直角边的等腰直角三角形,求拋物线的解析式;
为直角边的等腰直角三角形,求拋物线的解析式;
(3)过点 作
作 轴的垂线,交直线
轴的垂线,交直线 于点
于点 ,点
,点 恰好是线段
恰好是线段 三等分点且满足
三等分点且满足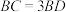 ,若抛物线与线段
,若抛物线与线段 只有一个公共点,结合函数的图象,直接写出
只有一个公共点,结合函数的图象,直接写出 的取值范围.
的取值范围.
 中,拋物线
中,拋物线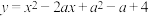 的顶点为
的顶点为 ,点
,点 为直线
为直线 上的两个动点(点
上的两个动点(点 在点
在点 的左侧),且
的左侧),且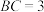 .
.(1)求点
 的坐标(用含
的坐标(用含 的代数式表示);
的代数式表示);(2)若
 是以
是以 为直角边的等腰直角三角形,求拋物线的解析式;
为直角边的等腰直角三角形,求拋物线的解析式;(3)过点
 作
作 轴的垂线,交直线
轴的垂线,交直线 于点
于点 ,点
,点 恰好是线段
恰好是线段 三等分点且满足
三等分点且满足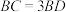 ,若抛物线与线段
,若抛物线与线段 只有一个公共点,结合函数的图象,直接写出
只有一个公共点,结合函数的图象,直接写出 的取值范围.
的取值范围.
您最近一年使用:0次

 是抛物线
是抛物线 上的两点,且
上的两点,且 .(O为原点)
.(O为原点)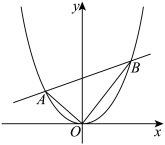
 是否恒过定点,若是,求出定点坐标,并说明理由.
是否恒过定点,若是,求出定点坐标,并说明理由. 面积的最小值;
面积的最小值;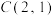 ,将
,将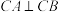 ,直线AB是否恒过定点?若是,直接写出定点坐标,不必说明理由.
,直线AB是否恒过定点?若是,直接写出定点坐标,不必说明理由.
 .
.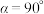 ,
, ,过
,过  于点
于点 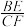 的值为 ;
的值为 ;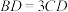 ,求
,求 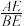 的值.
的值.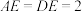 ,
,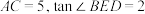 ,直接写出线段
,直接写出线段  的长度.
的长度.


