已知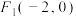 ,
,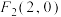 ,M是圆O:
,M是圆O: 上任意一点,
上任意一点, 关于点M的对称点为N,线段
关于点M的对称点为N,线段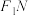 的垂直平分线与直线
的垂直平分线与直线 相交于点T,记点T的轨迹为曲线C.
相交于点T,记点T的轨迹为曲线C.
(1)求曲线C的方程;
(2)设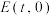 (
( )为曲线C上一点,不与x轴垂直的直线l与曲线C交于G,H两点(异于E点).若直线GE,HE的斜率之积为2,求证:直线l过定点.
)为曲线C上一点,不与x轴垂直的直线l与曲线C交于G,H两点(异于E点).若直线GE,HE的斜率之积为2,求证:直线l过定点.
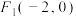 ,
,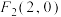 ,M是圆O:
,M是圆O: 上任意一点,
上任意一点, 关于点M的对称点为N,线段
关于点M的对称点为N,线段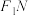 的垂直平分线与直线
的垂直平分线与直线 相交于点T,记点T的轨迹为曲线C.
相交于点T,记点T的轨迹为曲线C.(1)求曲线C的方程;
(2)设
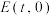 (
( )为曲线C上一点,不与x轴垂直的直线l与曲线C交于G,H两点(异于E点).若直线GE,HE的斜率之积为2,求证:直线l过定点.
)为曲线C上一点,不与x轴垂直的直线l与曲线C交于G,H两点(异于E点).若直线GE,HE的斜率之积为2,求证:直线l过定点.
2024·江西·二模 查看更多[4]
江西省重点中学盟校2024届高三第二次联考数学试题湖北省荆州市部分重点高中2024届高考适应性考试数学试题(已下线)模型8 与斜率和有关的定点定值问题模型(已下线)重难点突破16 圆锥曲线中的定点、定值问题(十二大题型)-2
更新时间:2024/05/14 19:03:41
|
相似题推荐
解答题-证明题
|
较难
(0.4)
名校
解题方法
【推荐1】已知圆 :
: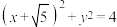 ,定点
,定点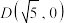 ,如图所示,圆
,如图所示,圆 上某一点
上某一点 恰好与点
恰好与点 关于直线
关于直线 对称,设直线
对称,设直线 与直线
与直线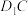 的交点为
的交点为 .
.
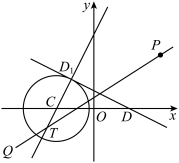
(1)求证: 为定值,并求出点
为定值,并求出点 的轨迹
的轨迹 方程;
方程;
(2)设 ,
, 为曲线
为曲线 上一点,
上一点, 为圆
为圆 上一点(
上一点( ,
, 均不在
均不在 轴上).直线
轴上).直线 ,
, 的斜率分别记为
的斜率分别记为 ,
, ,且
,且 .求证:直线
.求证:直线 过定点,并求出此定点的坐标.
过定点,并求出此定点的坐标.
 :
: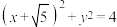 ,定点
,定点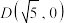 ,如图所示,圆
,如图所示,圆 上某一点
上某一点 恰好与点
恰好与点 关于直线
关于直线 对称,设直线
对称,设直线 与直线
与直线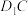 的交点为
的交点为 .
.
(1)求证:
 为定值,并求出点
为定值,并求出点 的轨迹
的轨迹 方程;
方程;(2)设
 ,
, 为曲线
为曲线 上一点,
上一点, 为圆
为圆 上一点(
上一点( ,
, 均不在
均不在 轴上).直线
轴上).直线 ,
, 的斜率分别记为
的斜率分别记为 ,
, ,且
,且 .求证:直线
.求证:直线 过定点,并求出此定点的坐标.
过定点,并求出此定点的坐标.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
名校
【推荐2】已知动点 分别与定点
分别与定点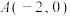 和
和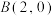 连线的斜率乘积
连线的斜率乘积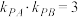 .
.
(1)求动点 的轨迹
的轨迹 ;
;
(2)设点 位于第一象限,
位于第一象限, 是
是 的右焦点,
的右焦点,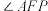 的平分线交
的平分线交 于点
于点 ,求证:
,求证: .
.
 分别与定点
分别与定点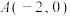 和
和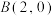 连线的斜率乘积
连线的斜率乘积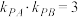 .
.(1)求动点
 的轨迹
的轨迹 ;
;(2)设点
 位于第一象限,
位于第一象限, 是
是 的右焦点,
的右焦点,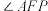 的平分线交
的平分线交 于点
于点 ,求证:
,求证: .
.
您最近一年使用:0次
【推荐1】已知双曲线 (
( ,
, )的离心率为2,且经过点
)的离心率为2,且经过点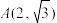 .
.
(1)求双曲线 的方程;
的方程;
(2)点 ,
, 在双曲线
在双曲线 上,且
上,且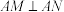 ,
, ,
, 为垂足.证明:①直线
为垂足.证明:①直线 过定点;②存在定点
过定点;②存在定点 ,使得
,使得 为定值.
为定值.
 (
( ,
, )的离心率为2,且经过点
)的离心率为2,且经过点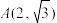 .
.(1)求双曲线
 的方程;
的方程;(2)点
 ,
, 在双曲线
在双曲线 上,且
上,且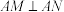 ,
, ,
, 为垂足.证明:①直线
为垂足.证明:①直线 过定点;②存在定点
过定点;②存在定点 ,使得
,使得 为定值.
为定值.
您最近一年使用:0次
【推荐2】设直线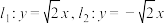 .点
.点 和点
和点 分别在直线
分别在直线 和
和 上运动,点
上运动,点 为
为 的中点,点
的中点,点 为坐标原点,且
为坐标原点,且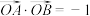 .
.
(1)求点 的轨迹方程
的轨迹方程 ;
;
(2)设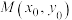 ,求当
,求当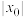 取得最小值时直线
取得最小值时直线 的方程;
的方程;
(3)设点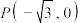 关于直线
关于直线 的对称点为
的对称点为 ,证明:直线
,证明:直线 过定点.
过定点.
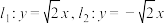 .点
.点 和点
和点 分别在直线
分别在直线 和
和 上运动,点
上运动,点 为
为 的中点,点
的中点,点 为坐标原点,且
为坐标原点,且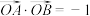 .
.(1)求点
 的轨迹方程
的轨迹方程 ;
;(2)设
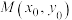 ,求当
,求当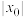 取得最小值时直线
取得最小值时直线 的方程;
的方程;(3)设点
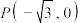 关于直线
关于直线 的对称点为
的对称点为 ,证明:直线
,证明:直线 过定点.
过定点.
您最近一年使用:0次
解答题-证明题
|
较难
(0.4)
名校
解题方法
【推荐1】已知圆 和定点
和定点 P是圆
P是圆 上任意一点,线段
上任意一点,线段 的垂直平分线交
的垂直平分线交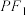 于点M,设动点M的轨迹为曲线E.
于点M,设动点M的轨迹为曲线E.
(1)求曲线E的方程;
(2)设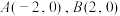 ,过
,过 的直线l交曲线E于M,N两点(点M在x轴上方),设直线AM与BN的斜率分别为
的直线l交曲线E于M,N两点(点M在x轴上方),设直线AM与BN的斜率分别为 ,求证:
,求证: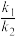 为定值.
为定值.
 和定点
和定点 P是圆
P是圆 上任意一点,线段
上任意一点,线段 的垂直平分线交
的垂直平分线交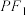 于点M,设动点M的轨迹为曲线E.
于点M,设动点M的轨迹为曲线E.(1)求曲线E的方程;
(2)设
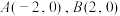 ,过
,过 的直线l交曲线E于M,N两点(点M在x轴上方),设直线AM与BN的斜率分别为
的直线l交曲线E于M,N两点(点M在x轴上方),设直线AM与BN的斜率分别为 ,求证:
,求证: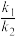 为定值.
为定值.
您最近一年使用:0次
解答题-问答题
|
较难
(0.4)
名校
解题方法
【推荐2】已知椭圆 :
: 的离心率为
的离心率为 ,其左、右焦点分别为
,其左、右焦点分别为 、
、 ,上顶点为
,上顶点为 ,且
,且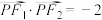 .
.
(1)求椭圆 的方程;
的方程;
(2)直线 :
: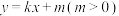 与椭圆
与椭圆 交于
交于 两点,О为坐标原点.试求当
两点,О为坐标原点.试求当 为何值时,
为何值时,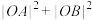 恒为定值,并求此时
恒为定值,并求此时 面积的最大值.
面积的最大值.
 :
: 的离心率为
的离心率为 ,其左、右焦点分别为
,其左、右焦点分别为 、
、 ,上顶点为
,上顶点为 ,且
,且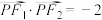 .
.(1)求椭圆
 的方程;
的方程;(2)直线
 :
: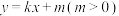 与椭圆
与椭圆 交于
交于 两点,О为坐标原点.试求当
两点,О为坐标原点.试求当 为何值时,
为何值时,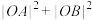 恒为定值,并求此时
恒为定值,并求此时 面积的最大值.
面积的最大值.
您最近一年使用:0次

 上的动点,点
上的动点,点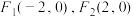 ,延长
,延长 至N,使得
至N,使得 ,线段
,线段 ,求
,求 的面积的最小值.
的面积的最小值.
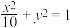 的左、右焦点F1,F2与双曲线
的左、右焦点F1,F2与双曲线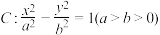 的焦点重合,且直线
的焦点重合,且直线 与双曲线右支相交于点P,当双曲线的离心率取最小值时.
与双曲线右支相交于点P,当双曲线的离心率取最小值时.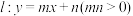 与双曲线C交于A1,B1两点,证明当
与双曲线C交于A1,B1两点,证明当 时,直线l过定点,并求出定点坐标.
时,直线l过定点,并求出定点坐标.
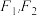 分别为椭圆
分别为椭圆 : 的左、右焦点,
: 的左、右焦点, 的面积为
的面积为 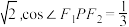 .
.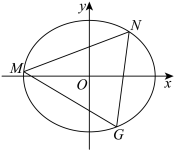
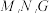 是椭圆上不重合的三点,原点
是椭圆上不重合的三点,原点 的重心
的重心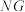 垂直于
垂直于 

