在数学建模课上,老师给大家带来了一则新闻:“2019年8月16日上午,423米的东莞第一高楼民盈国贸中心2号楼(以下简称“国贸中心”)正式封顶,随着最后一方混凝土浇筑到位,标志着东莞最高楼纪录诞生,由东莞本地航母级企业民盈集团刷新了东莞天际线,比之前的东莞第一高楼台商大厦高出134米.”在同学们的惊叹中,老师提出了问题:国贸中心真有这么高吗?我们能否运用所学知识测量验证一下?一周后,两个兴趣小组分享了他们各自的测量方案.
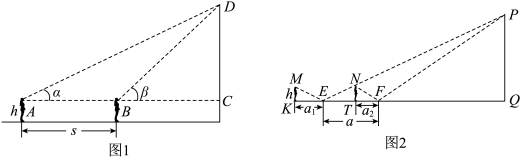
第一小组采用的是“两次测角法”:他们在国贸中心隔壁的会展中心广场上的 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为 ,正对国贸中心前进了
,正对国贸中心前进了 米后,到达
米后,到达 点,在
点,在 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为 ,然后计算出国贸中心的高度(如图).
,然后计算出国贸中心的高度(如图).
第二小组采用的是“镜面反射法”:在国贸中心后面的新世纪豪园一幢11层楼(与国贸中心处于同一水平面,每层约3米)楼顶天台上,进行两个操作步骤:①将平面镜置于天台地面上,人后退至从镜中能看到国贸大厦的顶部位置,测量出人与镜子的距离为 米;②正对国贸中心,将镜子前移
米;②正对国贸中心,将镜子前移 米,重复①中的操作,测量出人与镜子的距离为
米,重复①中的操作,测量出人与镜子的距离为 米.然后计算出国贸中心的高度(如图).
米.然后计算出国贸中心的高度(如图).
实际操作中,第一小组测得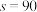 米,
米,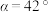 ,
,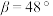 ,最终算得国贸中心高度为
,最终算得国贸中心高度为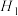 ;第二小组测得
;第二小组测得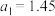 米,
米,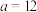 米,
米, 米,最终算得国贸中心高度为
米,最终算得国贸中心高度为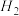 ;假设他们测量者的“眼高
;假设他们测量者的“眼高 ”都为
”都为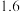 米.
米.
(1)请你用所学知识帮两个小组完成计算(参考数据: ,
, ,答案保留整数结果);
,答案保留整数结果);
(2)你认为哪个小组的方案更好,说出你的理由.
第一小组采用的是“两次测角法”:他们在国贸中心隔壁的会展中心广场上的
 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为 ,正对国贸中心前进了
,正对国贸中心前进了 米后,到达
米后,到达 点,在
点,在 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为 ,然后计算出国贸中心的高度(如图).
,然后计算出国贸中心的高度(如图).第二小组采用的是“镜面反射法”:在国贸中心后面的新世纪豪园一幢11层楼(与国贸中心处于同一水平面,每层约3米)楼顶天台上,进行两个操作步骤:①将平面镜置于天台地面上,人后退至从镜中能看到国贸大厦的顶部位置,测量出人与镜子的距离为
 米;②正对国贸中心,将镜子前移
米;②正对国贸中心,将镜子前移 米,重复①中的操作,测量出人与镜子的距离为
米,重复①中的操作,测量出人与镜子的距离为 米.然后计算出国贸中心的高度(如图).
米.然后计算出国贸中心的高度(如图).实际操作中,第一小组测得
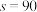 米,
米,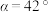 ,
,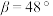 ,最终算得国贸中心高度为
,最终算得国贸中心高度为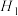 ;第二小组测得
;第二小组测得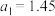 米,
米,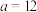 米,
米, 米,最终算得国贸中心高度为
米,最终算得国贸中心高度为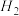 ;假设他们测量者的“眼高
;假设他们测量者的“眼高 ”都为
”都为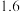 米.
米.
(1)请你用所学知识帮两个小组完成计算(参考数据:
 ,
, ,答案保留整数结果);
,答案保留整数结果);(2)你认为哪个小组的方案更好,说出你的理由.
19-20高二上·广东东莞·期末 查看更多[3]
广东省东莞市2019-2020学年高二上学期期末数学试题(已下线)【新教材精创】9.2正弦定理与余弦定理的应用(第1课时)练习(1)陕西省西安中学2019-2020学年高二上学期期末教学质量检查数学试题
更新时间:2020/01/23 20:55:15
|
相似题推荐
解答题-问答题
|
适中
(0.65)
名校
解题方法
【推荐1】山顶有一座石塔 ,已知石塔的高度为
,已知石塔的高度为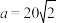 .
.
(1)如图,若以 ,
, 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点A的俯角为
处测得地面上一点A的俯角为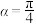 ,在塔底
,在塔底 处测得A处的俯角为
处测得A处的俯角为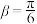 ,求山的高度
,求山的高度 .
.

(2)如图,若将观测点选在地面的直线 上,其中
上,其中 是塔顶
是塔顶 在地面上的正投影,当观测点
在地面上的正投影,当观测点 在
在 上满足
上满足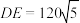 时,看
时,看 的视角(即点
的视角(即点 与点
与点 仰角的差
仰角的差 )最大,求山的高度
)最大,求山的高度 .
.
 ,已知石塔的高度为
,已知石塔的高度为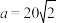 .
.(1)如图,若以
 ,
, 为观测点,在塔顶
为观测点,在塔顶 处测得地面上一点A的俯角为
处测得地面上一点A的俯角为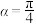 ,在塔底
,在塔底 处测得A处的俯角为
处测得A处的俯角为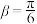 ,求山的高度
,求山的高度 .
.
(2)如图,若将观测点选在地面的直线
 上,其中
上,其中 是塔顶
是塔顶 在地面上的正投影,当观测点
在地面上的正投影,当观测点 在
在 上满足
上满足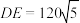 时,看
时,看 的视角(即点
的视角(即点 与点
与点 仰角的差
仰角的差 )最大,求山的高度
)最大,求山的高度 .
.
您最近一年使用:0次
解答题-问答题
|
适中
(0.65)
【推荐2】潍坊文化艺术中心的观光塔是潍坊市的标志性建筑,某班同学准备测量观光塔 的高度
的高度 (单位:米),如图所示,垂直放置的标杆
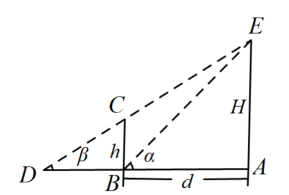
(单位:米),如图所示,垂直放置的标杆 的高度
的高度 米,已知
米,已知 ,
, .
.
(1)该班同学测得 一组数据,
一组数据, ,
, ,请据此算出
,请据此算出 的值;
的值;
(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离 (单位:米),使
(单位:米),使 与
与 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问 为多大时
为多大时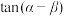 的值最大?
的值最大?
 的高度
的高度 (单位:米),如图所示,垂直放置的标杆
(单位:米),如图所示,垂直放置的标杆 的高度
的高度 米,已知
米,已知 ,
, .
.
(1)该班同学测得
 一组数据,
一组数据, ,
, ,请据此算出
,请据此算出 的值;
的值;(2)该班同学分析若干测得的数据后,发现适当调整标杆到观光塔的距离
 (单位:米),使
(单位:米),使 与
与 的差较大,可以提高测量精确度,若观光塔高度为136米,问
的差较大,可以提高测量精确度,若观光塔高度为136米,问 为多大时
为多大时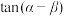 的值最大?
的值最大?
您最近一年使用:0次
解答题-应用题
|
适中
(0.65)
名校
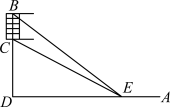
【推荐3】(1)某校运动会开幕式上举行升旗仪式,旗杆正好处在坡角为 的观礼台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部B的仰角分别为
的观礼台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部B的仰角分别为 和
和 ,第一排和最后一排的距离为
,第一排和最后一排的距离为 米(如图所示),旗杆底部与第一排在同一水平面上,若国歌播放的时间约为50秒,升旗手应以约多大的速度匀速升旗?
米(如图所示),旗杆底部与第一排在同一水平面上,若国歌播放的时间约为50秒,升旗手应以约多大的速度匀速升旗?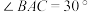 ,
,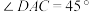 ,
, ,
,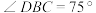 ,同时测得
,同时测得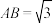 海里.求C,D之间的距离.
海里.求C,D之间的距离.
 的观礼台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部B的仰角分别为
的观礼台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部B的仰角分别为 和
和 ,第一排和最后一排的距离为
,第一排和最后一排的距离为 米(如图所示),旗杆底部与第一排在同一水平面上,若国歌播放的时间约为50秒,升旗手应以约多大的速度匀速升旗?
米(如图所示),旗杆底部与第一排在同一水平面上,若国歌播放的时间约为50秒,升旗手应以约多大的速度匀速升旗?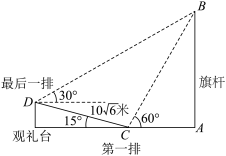
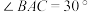 ,
,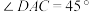 ,
, ,
,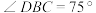 ,同时测得
,同时测得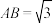 海里.求C,D之间的距离.
海里.求C,D之间的距离.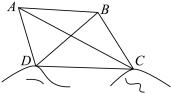
您最近一年使用:0次



