名校
1 . 对于函数 ,若
,若 ,则称
,则称 为
为 的“不动点”;若
的“不动点”;若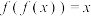 ,则称
,则称 为
为 的“稳定点”.函数
的“稳定点”.函数 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为 和
和 ,即
,即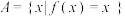 ,
, .
.
(1)求证: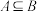 ;
;
(2)若 ,且
,且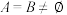 ,求实数
,求实数 的取值范围.
的取值范围.
 ,若
,若 ,则称
,则称 为
为 的“不动点”;若
的“不动点”;若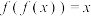 ,则称
,则称 为
为 的“稳定点”.函数
的“稳定点”.函数 的“不动点”和“稳定点”的集合分别记为
的“不动点”和“稳定点”的集合分别记为 和
和 ,即
,即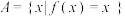 ,
, .
.(1)求证:
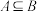 ;
;(2)若
 ,且
,且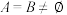 ,求实数
,求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2018-12-15更新
|
1781次组卷
|
7卷引用:2004年湖南省高中数学竞赛试题
2004年湖南省高中数学竞赛试题湖南省长沙市长郡中学2020-2021学年高一上学期适应性调查考试数学试题江西省景德镇一中2020-2021学年高一(2班)上学期期末考试数学试题(已下线)专题1.1—集合—2022届高三数学一轮复习精讲精练湖南省长沙市长郡中学2021-2022学年高一上学期第一次适应性调查数学试题(已下线)第1章集合与常用逻辑用语专练1 集合-2022届高三数学一轮复习(已下线)模块二 大招16 不动点与稳定点
名校
2 . 已知函数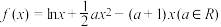 .
.
(Ⅰ)当 时,函数
时,函数 在区间
在区间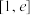 上的最小值为-5,求
上的最小值为-5,求 的值;
的值;
(Ⅱ)设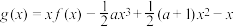 ,且
,且 有两个极值点
有两个极值点 ,
, .
.
(i)求实数 的取值范围;
的取值范围;
(ii)证明: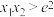 .
.
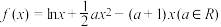 .
.(Ⅰ)当
 时,函数
时,函数 在区间
在区间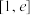 上的最小值为-5,求
上的最小值为-5,求 的值;
的值;(Ⅱ)设
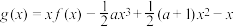 ,且
,且 有两个极值点
有两个极值点 ,
, .
.(i)求实数
 的取值范围;
的取值范围;(ii)证明:
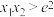 .
.
您最近一年使用:0次
2019-04-20更新
|
1985次组卷
|
5卷引用:贵州省凯里市第一中学2019届高三下学期模拟考试《黄金卷三》数学(理)试题
贵州省凯里市第一中学2019届高三下学期模拟考试《黄金卷三》数学(理)试题2020届陕西省西安交大附中学南校区高三上学期期中数学(理)试题2020届浙江省温州市新力量联盟高三上学期期末数学试题(已下线)专题10 导数与函数的极值、最值-冲刺2020高考跳出题海之高三数学模拟试题精中选萃(已下线)专题03 利用导数求函数的极值、最值(第六篇)-备战2020年高考数学大题精做之解答题题型全覆盖
名校
解题方法
3 . 已知函数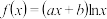 在
在 处的切线方程为
处的切线方程为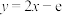
(1).求 的解析式;
的解析式;
(2).若对任意的 ,均有
,均有 求实数k的范围;
求实数k的范围;
(3).设 为两个正数,求证:
为两个正数,求证: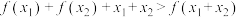
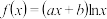 在
在 处的切线方程为
处的切线方程为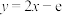
(1).求
 的解析式;
的解析式;(2).若对任意的
 ,均有
,均有 求实数k的范围;
求实数k的范围;(3).设
 为两个正数,求证:
为两个正数,求证: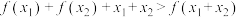
您最近一年使用:0次
4 . 设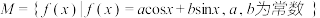 ,
, :把平面上任意一点
:把平面上任意一点 映射为函数
映射为函数 .
.
(1)证明:不存在两个不同的点对应于同一个函数;
(2)证明:当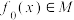 时,
时,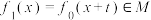 ,
, 为常数;
为常数;
(3)设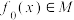 时,
时,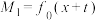 ,
,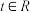 ,在映射
,在映射 的作用下,
的作用下, 作为像,求其原像,并说明它是什么图像?
作为像,求其原像,并说明它是什么图像?
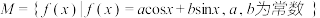 ,
, :把平面上任意一点
:把平面上任意一点 映射为函数
映射为函数 .
.(1)证明:不存在两个不同的点对应于同一个函数;
(2)证明:当
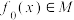 时,
时,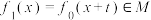 ,
, 为常数;
为常数;(3)设
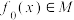 时,
时,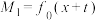 ,
,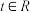 ,在映射
,在映射 的作用下,
的作用下, 作为像,求其原像,并说明它是什么图像?
作为像,求其原像,并说明它是什么图像?
您最近一年使用:0次



