名校
解题方法
1 . 矮化密植是指应用生物或栽培措施使果树生长树冠紧凑的方法,它与常规的矮小栽培相比有许多优势,如采用这种矮化果树可以建立比常规果园定植密度更高的果园,不仅能提高土壤及光能利用率,还能够获得更多的早期经济效益.某乡镇计划引进A,B两种矮化果树,已知A种矮化果树种植成功率为 ,成功后每公顷收益7.5万元;B种矮化果树种植成功率为
,成功后每公顷收益7.5万元;B种矮化果树种植成功率为 ,成功后每公顷收益9万元.假设种植不成功时,种植A,B两种矮化果树每公顷均损失1.5万元,每公顷是否种植成功相互独立.
,成功后每公顷收益9万元.假设种植不成功时,种植A,B两种矮化果树每公顷均损失1.5万元,每公顷是否种植成功相互独立.
(1)甲种植户试种两种矮化果树各1公顷,总收益为X万元,求X的分布列及数学期望;
(2)乙种植户有良田6公顷,本计划全部种植A,但是甲劝说乙应该种植两种矮化果树各3公顷,请按照总收益的角度分析一下,乙应选择哪一种方案?
 ,成功后每公顷收益7.5万元;B种矮化果树种植成功率为
,成功后每公顷收益7.5万元;B种矮化果树种植成功率为 ,成功后每公顷收益9万元.假设种植不成功时,种植A,B两种矮化果树每公顷均损失1.5万元,每公顷是否种植成功相互独立.
,成功后每公顷收益9万元.假设种植不成功时,种植A,B两种矮化果树每公顷均损失1.5万元,每公顷是否种植成功相互独立.(1)甲种植户试种两种矮化果树各1公顷,总收益为X万元,求X的分布列及数学期望;
(2)乙种植户有良田6公顷,本计划全部种植A,但是甲劝说乙应该种植两种矮化果树各3公顷,请按照总收益的角度分析一下,乙应选择哪一种方案?
您最近一年使用:0次
2024-01-10更新
|
382次组卷
|
5卷引用:2024届河南省名校学术联盟高考模拟信息卷&押题卷数学(三)
2024届河南省名校学术联盟高考模拟信息卷&押题卷数学(三)(已下线)第04讲 7.3.1离散型随机变量的均值-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)江西省南昌市第十九中学2023-2024学年高二上学期期末考试数学试卷(已下线)7.3.1 离散型随机变量的均值——课后作业(巩固版)(已下线)专题3.2离散型随机变量的分布列及数字特征(七个重难点突破)-2023-2024学年高二数学下学期重难点突破及混淆易错规避(人教A版2019)
名校
2 . 银行储蓄存款是一种风险较小的投资方式,将一定数额的本金存入银行,约定存期,到期后就可以得到相应的利息,从而获得收益,设存入银行的本金为P(元),存期为m(年),年化利率为r,则到期后的利息 (元).以下为上海某银行的存款利率:
(元).以下为上海某银行的存款利率:
(1)洪老师将10万元在上海某银行一次性存满二年,求到期后的本息和(本金与利息的总和);
(2)杜老师准备将10万元在上海某银行存三年,有以下三种方案:
方案①:一次性存满三年;
方案②:先存二年,再存一年;
方案③:先存一年,再续存一年,然后再续存一年;
通过计算三种方案的本息和(精确到小数点后2位)判断哪一种方案更合算,并基于该实际结果给予杜老师一般性的银行储蓄存款的建议.
 (元).以下为上海某银行的存款利率:
(元).以下为上海某银行的存款利率:| 存期 | 一年 | 二年 | 三年 |
| 年化利率 | 1.75% | 2.25% | 2.75% |
(2)杜老师准备将10万元在上海某银行存三年,有以下三种方案:
方案①:一次性存满三年;
方案②:先存二年,再存一年;
方案③:先存一年,再续存一年,然后再续存一年;
通过计算三种方案的本息和(精确到小数点后2位)判断哪一种方案更合算,并基于该实际结果给予杜老师一般性的银行储蓄存款的建议.
您最近一年使用:0次
2022-07-02更新
|
273次组卷
|
4卷引用:上海市建平中学2021-2022学年高一下学期期末数学试题
上海市建平中学2021-2022学年高一下学期期末数学试题(已下线)8.2 函数与数学模型 (1)(已下线)第14讲 函数的应用与反函数(3大考点)(2)江西省萍乡市上栗中学2022-2023学年高一上学期期末数学试题
名校
解题方法
3 . 直三棱柱 中,已知
中,已知 ,
, ,
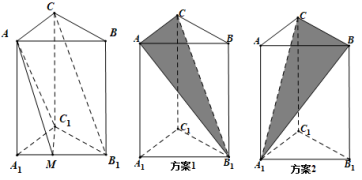
,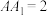 .
.
(1)若 为
为 的中点,求三棱锥
的中点,求三棱锥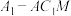 的体积,并证明:
的体积,并证明: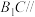 平面
平面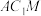 ;
;
(2)将两块形状与该直三棱柱完全相同的木料按如下图所示两种方案沿阴影面进行切割,把木料一分为二,留下体积较大的一块木料.根据你所学的知识,请判断采用哪一种方案会使留下的木料表面积较大,并求出这个较大的表面积和说明理由.
 中,已知
中,已知 ,
, ,
,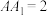 .
.
(1)若
 为
为 的中点,求三棱锥
的中点,求三棱锥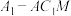 的体积,并证明:
的体积,并证明: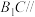 平面
平面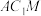 ;
;(2)将两块形状与该直三棱柱完全相同的木料按如下图所示两种方案沿阴影面进行切割,把木料一分为二,留下体积较大的一块木料.根据你所学的知识,请判断采用哪一种方案会使留下的木料表面积较大,并求出这个较大的表面积和说明理由.
您最近一年使用:0次
2021-10-29更新
|
374次组卷
|
6卷引用:湖南省永州市第一中学2020-2021学年高一下学期期中数学试题
湖南省永州市第一中学2020-2021学年高一下学期期中数学试题(已下线)8.5 空间直线、平面的平行广东省佛山市顺德区容山中学2021-2022学年高一下学期期中数学试题(已下线)13.3空间图形的表面积和体积-2021-2022学年高一数学10分钟课前预习练(苏教版2019必修第二册)2023版 湘教版(2019) 必修第二册 过关斩将 第4章 综合拔高练江西省宜春市清江中学2024届高三上学期期中数学试题
解题方法
4 . 某“双一流A类”大学就业部从该校2020年已就业的大学本科毕业生中随机抽取了100人进行问卷调查,其中一项是他们的月薪收入情况,调查发现,他们的月薪收入在1.65万元到2.35万元之间,根据统计数据分组,得到如下的频率直方图,同一组数据用该区间的中点值作代表.
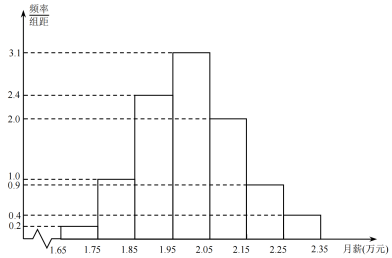
(1)求这100人月薪收入的样本平均数和样本方差;
(2)该校在某地区就业的2018届本科毕业生共50人,决定于2019年国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设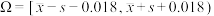 ,月薪落在区间Ω左侧的每人收取400元,月薪落在区间Ω内的每人收取600元,月薪落在区间Ω右侧的每人收取800元;
,月薪落在区间Ω左侧的每人收取400元,月薪落在区间Ω内的每人收取600元,月薪落在区间Ω右侧的每人收取800元;
方案二:按每人个月薪水的3%收取.
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用.
参考数据: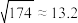 .
.

(1)求这100人月薪收入的样本平均数和样本方差;
(2)该校在某地区就业的2018届本科毕业生共50人,决定于2019年国庆长假期间举办一次同学联谊会,并收取一定的活动费用,有两种收费方案:
方案一:设
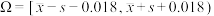 ,月薪落在区间Ω左侧的每人收取400元,月薪落在区间Ω内的每人收取600元,月薪落在区间Ω右侧的每人收取800元;
,月薪落在区间Ω左侧的每人收取400元,月薪落在区间Ω内的每人收取600元,月薪落在区间Ω右侧的每人收取800元;方案二:按每人个月薪水的3%收取.
用该校就业部统计的这100人月薪收入的样本频率进行估算,哪一种收费方案能收到更多的费用.
参考数据:
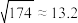 .
.
您最近一年使用:0次
2022-08-21更新
|
641次组卷
|
5卷引用:苏教版(2019) 必修第二册 过关斩将 第14章 本章达标检测
苏教版(2019) 必修第二册 过关斩将 第14章 本章达标检测(已下线)湖南省怀化市2022-2023学年高三上学期期末数学试题变式题17-22(已下线)9.2.4 总体离散程度的估计(精讲)-【精讲精练】2022-2023学年高一数学下学期同步精讲精练(人教A版2019必修第二册)(已下线)第39讲 频率分布直方图、总体取值规律、总体百分位数的估计5种常考题型)第六章 统计(综合检测卷)-2022-2023学年高一数学北师大版2019必修第一册
名校
解题方法
5 . 统计某公司 名推销员的月销售额(单位:千元)得到如下频率分布直方图.
名推销员的月销售额(单位:千元)得到如下频率分布直方图.
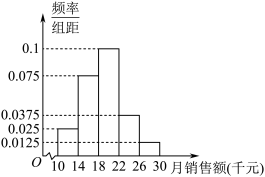
(1)同一组数据用该区间的中间值作代表,求这 名推销员的月销售额的平均数
名推销员的月销售额的平均数 与方差
与方差 ;
;
(2)请根据这组数据提出使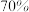 的推销员能够完成销售指标的建议;
的推销员能够完成销售指标的建议;
(3)现有两种奖励机制:
方案一:设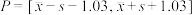 ,销售额落在
,销售额落在 左侧,每人每月奖励
左侧,每人每月奖励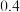 千元;销售额落在
千元;销售额落在 内,每人每月奖励
内,每人每月奖励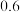 千元;销售额落在
千元;销售额落在 右侧,每人每月奖励
右侧,每人每月奖励 千元.
千元.
方案二:每人每月奖励其月销售额的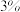 .
.
用统计的频率进行估算,选择哪一种方案公司需提供更多的奖励金?(参考数据: )
)
记: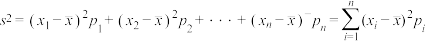 (其中
(其中 为
为 对应的频率).
对应的频率).
 名推销员的月销售额(单位:千元)得到如下频率分布直方图.
名推销员的月销售额(单位:千元)得到如下频率分布直方图.
(1)同一组数据用该区间的中间值作代表,求这
 名推销员的月销售额的平均数
名推销员的月销售额的平均数 与方差
与方差 ;
;(2)请根据这组数据提出使
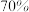 的推销员能够完成销售指标的建议;
的推销员能够完成销售指标的建议;(3)现有两种奖励机制:
方案一:设
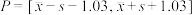 ,销售额落在
,销售额落在 左侧,每人每月奖励
左侧,每人每月奖励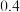 千元;销售额落在
千元;销售额落在 内,每人每月奖励
内,每人每月奖励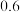 千元;销售额落在
千元;销售额落在 右侧,每人每月奖励
右侧,每人每月奖励 千元.
千元.方案二:每人每月奖励其月销售额的
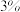 .
.用统计的频率进行估算,选择哪一种方案公司需提供更多的奖励金?(参考数据:
 )
)记:
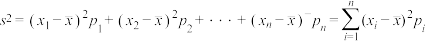 (其中
(其中 为
为 对应的频率).
对应的频率).
您最近一年使用:0次
2021-06-23更新
|
1346次组卷
|
5卷引用:河南名校联盟2020-2021学年高一下学期期中考试数学(文)试题
河南名校联盟2020-2021学年高一下学期期中考试数学(文)试题福建省泉州市永春第一中学2020-2021学年高一下学期期末数学试题(已下线)第九章 统计(选拔卷)-【单元测试】2021-2022学年高一数学尖子生选拔卷(人教A版2019必修第二册)江西省遂川中学2021-2022学年高一上学期第一次月考数学试题(A卷)黑龙江省哈尔滨市第四中学校2022-2023学年高二上学期第一次月考数学试题
6 . 某高校为了更好的掌握学校毕业生的发展情况成立了校友联络部,调查统计学生毕业后的就业、收入、发展、职业幸福感等情况,校友联络部在2020年已就业的毕业生中随机抽取了 人进行了问卷调查,经调查统计发现,他们的月薪在
人进行了问卷调查,经调查统计发现,他们的月薪在 元到
元到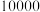 元(不含
元(不含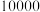 元)之间,经调查问卷数据表按照第
元)之间,经调查问卷数据表按照第 组
组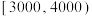 ,第
,第 组
组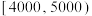 ,第
,第 组
组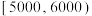 ,第
,第 组
组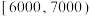 ,第
,第 组
组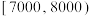 ,第
,第 组
组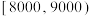 ,第
,第 组
组 绘制成如下的频率分布直方图;
绘制成如下的频率分布直方图;

若月薪落在区间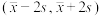 的左侧,则认为该毕业生属“就业不理想”的学生,学校将联系本人,从而为毕业生就业提供更好的指导意见,其中
的左侧,则认为该毕业生属“就业不理想”的学生,学校将联系本人,从而为毕业生就业提供更好的指导意见,其中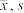 分别为样本平均数和样本标准差,已知
分别为样本平均数和样本标准差,已知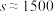 元.
元.
(1)现该校毕业生小李月薪为 元,试判断小李是否属于“就业不理想”的学生;
元,试判断小李是否属于“就业不理想”的学生;
(2)为感谢同学们对这项调查工作的支持,校友联络部现利用分层抽样的方法从样本的第 组和第
组和第 组中抽取
组中抽取 人,各赠送一份礼品,并从这
人,各赠送一份礼品,并从这 人中再抽取
人中再抽取 人,各赠送某款智能手机
人,各赠送某款智能手机 部,求获赠智能手机的
部,求获赠智能手机的 人中恰有
人中恰有 个人月薪少于
个人月薪少于 元的概率;
元的概率;
(3)位于省会城市的该校毕业生共 人,他们决定于2021年元旦期间举办一次校友会,并收取一定的活动经费,假定这
人,他们决定于2021年元旦期间举办一次校友会,并收取一定的活动经费,假定这 人所抽取样本中的
人所抽取样本中的 人月薪分布情况相同,并用样本频率进行估计,现有两种收费方案:
人月薪分布情况相同,并用样本频率进行估计,现有两种收费方案:
方案一:按每人一个月薪水的 收取(同一组中的数据用该组区间的中点值代表);
收取(同一组中的数据用该组区间的中点值代表);
方案二:月薪不低于 元的每人收取
元的每人收取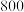 元,月薪不低于
元,月薪不低于 元但低于
元但低于 元的每人收取
元的每人收取 元,月薪低于
元,月薪低于 元的不收取任何费用.
元的不收取任何费用.
问:哪一种收费方案最终总费用更少?
 人进行了问卷调查,经调查统计发现,他们的月薪在
人进行了问卷调查,经调查统计发现,他们的月薪在 元到
元到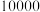 元(不含
元(不含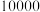 元)之间,经调查问卷数据表按照第
元)之间,经调查问卷数据表按照第 组
组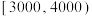 ,第
,第 组
组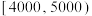 ,第
,第 组
组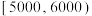 ,第
,第 组
组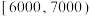 ,第
,第 组
组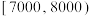 ,第
,第 组
组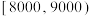 ,第
,第 组
组 绘制成如下的频率分布直方图;
绘制成如下的频率分布直方图;
若月薪落在区间
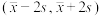 的左侧,则认为该毕业生属“就业不理想”的学生,学校将联系本人,从而为毕业生就业提供更好的指导意见,其中
的左侧,则认为该毕业生属“就业不理想”的学生,学校将联系本人,从而为毕业生就业提供更好的指导意见,其中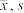 分别为样本平均数和样本标准差,已知
分别为样本平均数和样本标准差,已知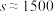 元.
元.(1)现该校毕业生小李月薪为
 元,试判断小李是否属于“就业不理想”的学生;
元,试判断小李是否属于“就业不理想”的学生;(2)为感谢同学们对这项调查工作的支持,校友联络部现利用分层抽样的方法从样本的第
 组和第
组和第 组中抽取
组中抽取 人,各赠送一份礼品,并从这
人,各赠送一份礼品,并从这 人中再抽取
人中再抽取 人,各赠送某款智能手机
人,各赠送某款智能手机 部,求获赠智能手机的
部,求获赠智能手机的 人中恰有
人中恰有 个人月薪少于
个人月薪少于 元的概率;
元的概率; (3)位于省会城市的该校毕业生共
 人,他们决定于2021年元旦期间举办一次校友会,并收取一定的活动经费,假定这
人,他们决定于2021年元旦期间举办一次校友会,并收取一定的活动经费,假定这 人所抽取样本中的
人所抽取样本中的 人月薪分布情况相同,并用样本频率进行估计,现有两种收费方案:
人月薪分布情况相同,并用样本频率进行估计,现有两种收费方案:方案一:按每人一个月薪水的
 收取(同一组中的数据用该组区间的中点值代表);
收取(同一组中的数据用该组区间的中点值代表);方案二:月薪不低于
 元的每人收取
元的每人收取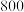 元,月薪不低于
元,月薪不低于 元但低于
元但低于 元的每人收取
元的每人收取 元,月薪低于
元,月薪低于 元的不收取任何费用.
元的不收取任何费用.问:哪一种收费方案最终总费用更少?
您最近一年使用:0次
2021-01-23更新
|
353次组卷
|
2卷引用:辽宁省葫芦岛市2020-2021学年高一上学期期末考试数学试题
名校
解题方法
7 . 某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如图所示:
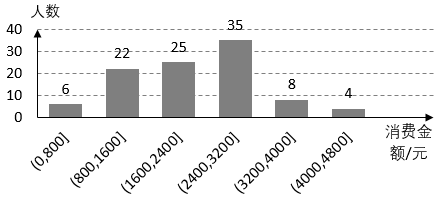
(1)现从去年的消费金额超过3 200元的消费者中随机抽取2人,求至少有1位消费者去年的消费金额在(3 200,4 000]内的概率;
(2)针对这些消费者,该健身机构今年欲实施入会制,详情如下表:
预计去年消费金额在(0,1 600]内的消费者今年都将会申请办理普通会员,消费金额在(1 600,3 200]内的消费者都将会申请办理银卡会员,消费金额在(3 200,4 800]内的消费者都将会申请办理金卡会员,消费者在申请办理会员时,需一次性缴清相应等级的消费金额,该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
方案1:按分层抽样从普通会员,银卡会员,金卡会员中总共抽取25位“幸运之星”给予奖励:普通会员中的“幸运之星”每人奖励500元;银卡会员中的“幸运之星”每人奖励600元;金卡会员中的“幸运之星”每人奖励800元.
方案2:每位会员均可参加摸奖游戏,游戏规则如下:从一个装有3个白球、2个红球(球只有颜色不同)的箱子中,有放回地摸三次球,每次只能摸一个球,若摸到红球的总数为2,则可获得200元奖励金;若摸到红球的总数为3,则可获得300元奖励金;其他情况不给予奖励.规定每位普通会员均可参加1次摸奖游戏;每位银卡会员均可参加2次摸奖游戏;每位金卡会员均可参加3次摸奖游戏(每次摸奖的结果相互独立).请你预测哪一种返利活动方案该健身机构的投资较少?并说明理由.

(1)现从去年的消费金额超过3 200元的消费者中随机抽取2人,求至少有1位消费者去年的消费金额在(3 200,4 000]内的概率;
(2)针对这些消费者,该健身机构今年欲实施入会制,详情如下表:
会员等级 | 消费金额 |
普通会员 | 2 000 |
银卡会员 | 2 700 |
金卡会员 | 3 200 |
方案1:按分层抽样从普通会员,银卡会员,金卡会员中总共抽取25位“幸运之星”给予奖励:普通会员中的“幸运之星”每人奖励500元;银卡会员中的“幸运之星”每人奖励600元;金卡会员中的“幸运之星”每人奖励800元.
方案2:每位会员均可参加摸奖游戏,游戏规则如下:从一个装有3个白球、2个红球(球只有颜色不同)的箱子中,有放回地摸三次球,每次只能摸一个球,若摸到红球的总数为2,则可获得200元奖励金;若摸到红球的总数为3,则可获得300元奖励金;其他情况不给予奖励.规定每位普通会员均可参加1次摸奖游戏;每位银卡会员均可参加2次摸奖游戏;每位金卡会员均可参加3次摸奖游戏(每次摸奖的结果相互独立).请你预测哪一种返利活动方案该健身机构的投资较少?并说明理由.
您最近一年使用:0次
2021-01-12更新
|
915次组卷
|
5卷引用:黑龙江省哈尔滨市第六中学2019届高三第二次模拟考试数学(理)试题
黑龙江省哈尔滨市第六中学2019届高三第二次模拟考试数学(理)试题黑龙江省大庆市第四中学2020届高三4月月考数学(理)试题(已下线)第09章+统计(B卷提高篇)-2020-2021学年高一数学必修第二册同步单元AB卷(新教材人教A版)(已下线)专题11.5 离散型随机变量的分布列、均值与方差(精讲)-2021年高考数学(理)一轮复习学与练(已下线)热点10 概率与统计-2020年高考数学(理)【热点·重点·难点】专练
名校
解题方法
8 . 某新型双轴承电动机需要装配两个轴承才能正常工作,且两个轴承互不影响.现计划购置甲,乙两个品牌的轴承,两个品牌轴承的使用寿命及价格情况如下表:
已知甲品牌使用 个月或
个月或 个月的概率均为
个月的概率均为 ,乙品牌使用
,乙品牌使用 个月或
个月或 个月的概率均为
个月的概率均为 .
.
(1)若从 件甲品牌和
件甲品牌和 件乙品牌共
件乙品牌共 件轴承中,任选
件轴承中,任选 件装入电动机内,求电动机可工作时间不少于
件装入电动机内,求电动机可工作时间不少于 个月的概率;
个月的概率;
(2)现有两种购置方案,方案一:购置 件甲品牌;方案二:购置
件甲品牌;方案二:购置 件甲品牌和
件甲品牌和 件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
品牌 | 价格(元/件) | 使用寿命(月) |
甲 |
|
|
乙 |
|
|
 个月或
个月或 个月的概率均为
个月的概率均为 ,乙品牌使用
,乙品牌使用 个月或
个月或 个月的概率均为
个月的概率均为 .
.(1)若从
 件甲品牌和
件甲品牌和 件乙品牌共
件乙品牌共 件轴承中,任选
件轴承中,任选 件装入电动机内,求电动机可工作时间不少于
件装入电动机内,求电动机可工作时间不少于 个月的概率;
个月的概率;(2)现有两种购置方案,方案一:购置
 件甲品牌;方案二:购置
件甲品牌;方案二:购置 件甲品牌和
件甲品牌和 件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
件乙品牌(甲、乙两品牌轴承搭配使用).试从性价比(即电动机正常工作时间与购置轴承的成本之比)的角度考虑,选择哪一种方案更实惠?
您最近一年使用:0次
2021-04-29更新
|
2661次组卷
|
6卷引用:山东省泰安市2021届高三二模数学试题
山东省泰安市2021届高三二模数学试题湖南省长沙市雅礼中学2021-2022学年高三上学期入学考试数学试题(已下线)第51讲 概率与统计综合问题-2022年新高考数学二轮专题突破精练山西省运城市芮城中学2021-2022学年高二下学期第一次月考数学试题人教A版(2019) 选修第三册 过关斩将 第七章 7.3.1 离散型随机变量的均值(已下线)专题13 概率综合问题-2021-2022学年高二数学下学期期末必考题型归纳及过关测试(人教A版2019)
2023·全国·模拟预测
解题方法
9 . 为了响应政府号召,增加农民收入,某村委会指导当地村民在果园里进行生态鸡的养殖,在2023年8月初,为了解所养殖的生态鸡的质量(单位;kg)情况,养殖负责人随机抓取了一部分鸡进行称重,得到如下频率分布直方图(同一组中的数据用该组区间的中点值代替),以样本估计总体.

(1)求养殖的生态鸡的质量的平均值.
(2)该地现养殖有5000只鸡,为了减轻养殖的压力,养殖负责人计划卖掉一部分鸡,另一部分计划春节再卖掉.若现在卖掉,价格为20元/kg,到春节卖掉,预估价格为22元/kg.现有以下两种方案:
方案一:体重不低于2.5kg的现在卖掉,其余的养殖到春节再卖掉,剩余的鸡平均每只需要10元养殖费用,到春节时,平均质量可以达到2.5kg;
方案二:体重不低于2kg的现在卖掉,其余的养殖到春节再卖掉,剩余的鸡平均每只需要10元养殖费用,到春节时,平均质量可以达到3kg.
从经济收益的角度来看,选择哪种方案更合适?

(1)求养殖的生态鸡的质量的平均值.
(2)该地现养殖有5000只鸡,为了减轻养殖的压力,养殖负责人计划卖掉一部分鸡,另一部分计划春节再卖掉.若现在卖掉,价格为20元/kg,到春节卖掉,预估价格为22元/kg.现有以下两种方案:
方案一:体重不低于2.5kg的现在卖掉,其余的养殖到春节再卖掉,剩余的鸡平均每只需要10元养殖费用,到春节时,平均质量可以达到2.5kg;
方案二:体重不低于2kg的现在卖掉,其余的养殖到春节再卖掉,剩余的鸡平均每只需要10元养殖费用,到春节时,平均质量可以达到3kg.
从经济收益的角度来看,选择哪种方案更合适?
您最近一年使用:0次
名校
解题方法
10 . 某地计划在一处海滩建造一个养殖场.
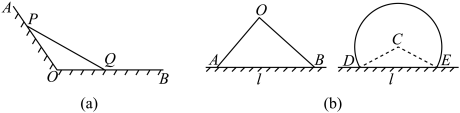
(1)如图(a)所示,射线 、
、 为海岸线,
为海岸线,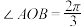 ,用长度为
,用长度为 的围网
的围网 依托海岸线围成一个
依托海岸线围成一个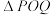 的养殖场,问如何选取点P、Q,才能使养殖场
的养殖场,问如何选取点P、Q,才能使养殖场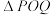 的面积最大,并求最大面积.
的面积最大,并求最大面积.
(2)如图(b所示,直线l为海岸线,现用长度为 的围网依托海岸线围成一个养殖场.
的围网依托海岸线围成一个养殖场.
方案一:围成三角形 (点A、B在直线l上),使三角形
(点A、B在直线l上),使三角形 面积最大,设其为
面积最大,设其为 ;
;
方案二:围成弓形 (点D、E在直线l上,C是优弧
(点D、E在直线l上,C是优弧 所在圆的圆心且
所在圆的圆心且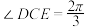 ),面积为
),面积为 .
.
试求出 的最大值和
的最大值和 (均精确到
(均精确到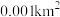 ),并指出哪一种设计方案更好.
),并指出哪一种设计方案更好.

(1)如图(a)所示,射线
 、
、 为海岸线,
为海岸线,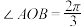 ,用长度为
,用长度为 的围网
的围网 依托海岸线围成一个
依托海岸线围成一个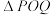 的养殖场,问如何选取点P、Q,才能使养殖场
的养殖场,问如何选取点P、Q,才能使养殖场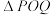 的面积最大,并求最大面积.
的面积最大,并求最大面积.(2)如图(b所示,直线l为海岸线,现用长度为
 的围网依托海岸线围成一个养殖场.
的围网依托海岸线围成一个养殖场.方案一:围成三角形
 (点A、B在直线l上),使三角形
(点A、B在直线l上),使三角形 面积最大,设其为
面积最大,设其为 ;
;方案二:围成弓形
 (点D、E在直线l上,C是优弧
(点D、E在直线l上,C是优弧 所在圆的圆心且
所在圆的圆心且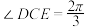 ),面积为
),面积为 .
.试求出
 的最大值和
的最大值和 (均精确到
(均精确到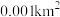 ),并指出哪一种设计方案更好.
),并指出哪一种设计方案更好.
您最近一年使用:0次
2021-03-23更新
|
169次组卷
|
4卷引用:沪教版(2020) 必修第二册 高效课堂 第六章 三角 6.4 复习与小结(1)



