1 . 2021年7月20日,佛山正式印发了《城市“畅通工程”两年行动方案》(以下简称《方案》),聚焦人民群众反映强烈的城市交通拥堵问题,通过微改造、微调整,为市民出行创造更加畅通有序的交通环境.现某医院附近有条长500米,宽6米的道路(如图1所示的矩形ABCD),改造前,路的一侧划有100个长5米,宽2.5米的停车位(如矩形AEFG),按《方案》,在不改变停车位形状大小、不改变汽车通道宽度的条件下,可通过压缩道路旁边绿化带及改变停车位方向来增加停车位,记绿化带被压缩的宽度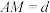 (米),停车位相对道路倾斜的角度
(米),停车位相对道路倾斜的角度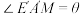 ,其中
,其中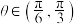 .
.
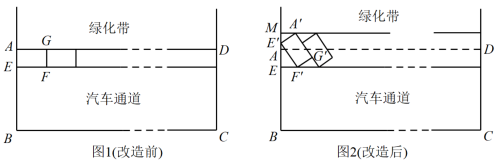
(1)求d关于 的函数表达式
的函数表达式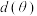 ;
;
(2)若 ,求该路段改造后的停车位比改造前增加的个数.
,求该路段改造后的停车位比改造前增加的个数.
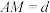 (米),停车位相对道路倾斜的角度
(米),停车位相对道路倾斜的角度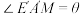 ,其中
,其中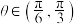 .
.
(1)求d关于
 的函数表达式
的函数表达式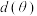 ;
;(2)若
 ,求该路段改造后的停车位比改造前增加的个数.
,求该路段改造后的停车位比改造前增加的个数.
您最近一年使用:0次
2022-07-07更新
|
608次组卷
|
4卷引用:广东省佛山市2021-2022学年高一下学期期末数学试题
广东省佛山市2021-2022学年高一下学期期末数学试题广东省惠州市惠州中学2022-2023学年高一下学期期中数学试题第7章 三角函数 单元综合检测(难点)-2022-2023学年高一数学《基础·重点·难点 》全面题型高分突破(苏教版2019必修第一册)(已下线)期末专题02 三角函数5.4-5.7大题综合-【备战期末必刷真题】
名校
2 . 如图,某公园改建一个三角形池塘, ,
, 百米,
百米, 百米,现准备养一批观赏鱼供游客观赏.
百米,现准备养一批观赏鱼供游客观赏.
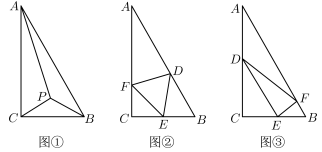
(1)若在△ABC内部取一点P,建造连廊供游客观赏,方案一如图①,使得点P是等腰三角形PBC的顶点,且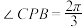 ,求连廊
,求连廊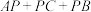 的长(单位为百米);
的长(单位为百米);
(2)若分别在AB,BC,CA上取点D,E,F,并建造连廊,使得△DEF变成池中池,放养更名贵的鱼类供游客观赏:方案二如图②,使得△DEF为正三角形,设 为图②中△DEF的面积,求
为图②中△DEF的面积,求 的最小值;方案三如图③,使得DE平行于AB,且EF垂直于DE,设
的最小值;方案三如图③,使得DE平行于AB,且EF垂直于DE,设 为图③中△DEF的面积,求
为图③中△DEF的面积,求 的取值范围.
的取值范围.
 ,
, 百米,
百米, 百米,现准备养一批观赏鱼供游客观赏.
百米,现准备养一批观赏鱼供游客观赏.
(1)若在△ABC内部取一点P,建造连廊供游客观赏,方案一如图①,使得点P是等腰三角形PBC的顶点,且
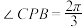 ,求连廊
,求连廊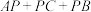 的长(单位为百米);
的长(单位为百米);(2)若分别在AB,BC,CA上取点D,E,F,并建造连廊,使得△DEF变成池中池,放养更名贵的鱼类供游客观赏:方案二如图②,使得△DEF为正三角形,设
 为图②中△DEF的面积,求
为图②中△DEF的面积,求 的最小值;方案三如图③,使得DE平行于AB,且EF垂直于DE,设
的最小值;方案三如图③,使得DE平行于AB,且EF垂直于DE,设 为图③中△DEF的面积,求
为图③中△DEF的面积,求 的取值范围.
的取值范围.
您最近一年使用:0次
2022-07-02更新
|
2578次组卷
|
8卷引用:广东省五校(广州市第二中学等)2021-2022学年高一下学期期末联考数学试题
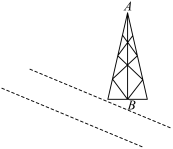
3 . 如图,要测量河对岸的塔高 .请设计一个方案,包括:(1)指出需要测量的数据(用字母表示,并在图中标出):(2)用文字和公式写出计算
.请设计一个方案,包括:(1)指出需要测量的数据(用字母表示,并在图中标出):(2)用文字和公式写出计算 的长的步骤.
的长的步骤.
 .请设计一个方案,包括:(1)指出需要测量的数据(用字母表示,并在图中标出):(2)用文字和公式写出计算
.请设计一个方案,包括:(1)指出需要测量的数据(用字母表示,并在图中标出):(2)用文字和公式写出计算 的长的步骤.
的长的步骤.
您最近一年使用:0次
2021-08-20更新
|
387次组卷
|
2卷引用:广东省佛山市南海区2020-2021学年高一下学期期末数学试题
4 . 已知 分别为
分别为 的三个内角
的三个内角 的对边,
的对边, 且
且 .
.
(1)求 ;
;
(2)给出三个条件:① ;②AC边上的中线为
;②AC边上的中线为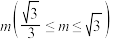 ;③
;③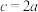 试从中选出两个可以确定
试从中选出两个可以确定 的条件,写出你的选择并以此为依据求c的值(只需写出二个选定方案即可).
的条件,写出你的选择并以此为依据求c的值(只需写出二个选定方案即可).
 分别为
分别为 的三个内角
的三个内角 的对边,
的对边, 且
且 .
.(1)求
 ;
;(2)给出三个条件:①
 ;②AC边上的中线为
;②AC边上的中线为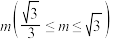 ;③
;③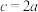 试从中选出两个可以确定
试从中选出两个可以确定 的条件,写出你的选择并以此为依据求c的值(只需写出二个选定方案即可).
的条件,写出你的选择并以此为依据求c的值(只需写出二个选定方案即可).
您最近一年使用:0次
11-12高三上·安徽六安·期中
名校
5 . 如图,现有一块半径为2m,圆心角为 的扇形铁皮
的扇形铁皮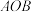 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形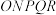 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形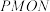 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形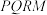 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形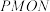 的面积达到最大,在此前提下,再使直角梯形
的面积达到最大,在此前提下,再使直角梯形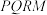 的面积也达到最大.
的面积也达到最大.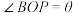 ,当矩形
,当矩形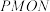 的面积最大时,求
的面积最大时,求 的值;
的值;
(2)求按这种裁剪方法的原材料利用率.
 的扇形铁皮
的扇形铁皮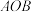 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形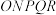 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形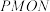 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形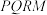 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形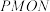 的面积达到最大,在此前提下,再使直角梯形
的面积达到最大,在此前提下,再使直角梯形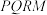 的面积也达到最大.
的面积也达到最大.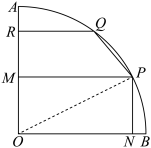
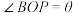 ,当矩形
,当矩形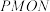 的面积最大时,求
的面积最大时,求 的值;
的值;(2)求按这种裁剪方法的原材料利用率.
您最近一年使用:0次
2016-12-01更新
|
1085次组卷
|
4卷引用:广东省汕头市金山中学2020-2021学年高一上学期期末数学试题
广东省汕头市金山中学2020-2021学年高一上学期期末数学试题河南省郑州市外国语中学2017-2018学年高一下学期期中数学试题山东省临沂第十八中学2023-2024学年高一下学期3月阶段性测试数学试题(已下线)2012届安徽省舒城中学高三第一学期期中考试理科数学



