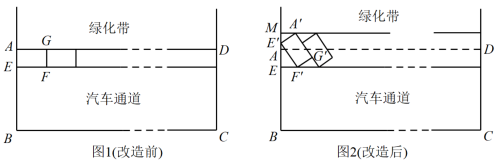
1 . 2021年7月20日,佛山正式印发了《城市“畅通工程”两年行动方案》(以下简称《方案》),聚焦人民群众反映强烈的城市交通拥堵问题,通过微改造、微调整,为市民出行创造更加畅通有序的交通环境.现某医院附近有条长500米,宽6米的道路(如图1所示的矩形ABCD),改造前,路的一侧划有100个长5米,宽2.5米的停车位(如矩形AEFG),按《方案》,在不改变停车位形状大小、不改变汽车通道宽度的条件下,可通过压缩道路旁边绿化带及改变停车位方向来增加停车位,记绿化带被压缩的宽度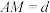 (米),停车位相对道路倾斜的角度
(米),停车位相对道路倾斜的角度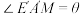 ,其中
,其中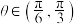 .
.
(1)求d关于 的函数表达式
的函数表达式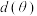 ;
;
(2)若 ,求该路段改造后的停车位比改造前增加的个数.
,求该路段改造后的停车位比改造前增加的个数.
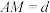 (米),停车位相对道路倾斜的角度
(米),停车位相对道路倾斜的角度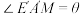 ,其中
,其中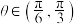 .
.
(1)求d关于
 的函数表达式
的函数表达式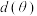 ;
;(2)若
 ,求该路段改造后的停车位比改造前增加的个数.
,求该路段改造后的停车位比改造前增加的个数.
您最近一年使用:0次
2022-07-07更新
|
608次组卷
|
4卷引用:广东省佛山市2021-2022学年高一下学期期末数学试题
广东省佛山市2021-2022学年高一下学期期末数学试题广东省惠州市惠州中学2022-2023学年高一下学期期中数学试题第7章 三角函数 单元综合检测(难点)-2022-2023学年高一数学《基础·重点·难点 》全面题型高分突破(苏教版2019必修第一册)(已下线)期末专题02 三角函数5.4-5.7大题综合-【备战期末必刷真题】
名校
2 . 如图,某公园改建一个三角形池塘, ,
, 百米,
百米, 百米,现准备养一批观赏鱼供游客观赏.
百米,现准备养一批观赏鱼供游客观赏.
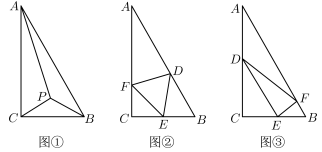
(1)若在△ABC内部取一点P,建造连廊供游客观赏,方案一如图①,使得点P是等腰三角形PBC的顶点,且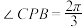 ,求连廊
,求连廊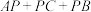 的长(单位为百米);
的长(单位为百米);
(2)若分别在AB,BC,CA上取点D,E,F,并建造连廊,使得△DEF变成池中池,放养更名贵的鱼类供游客观赏:方案二如图②,使得△DEF为正三角形,设 为图②中△DEF的面积,求
为图②中△DEF的面积,求 的最小值;方案三如图③,使得DE平行于AB,且EF垂直于DE,设
的最小值;方案三如图③,使得DE平行于AB,且EF垂直于DE,设 为图③中△DEF的面积,求
为图③中△DEF的面积,求 的取值范围.
的取值范围.
 ,
, 百米,
百米, 百米,现准备养一批观赏鱼供游客观赏.
百米,现准备养一批观赏鱼供游客观赏.
(1)若在△ABC内部取一点P,建造连廊供游客观赏,方案一如图①,使得点P是等腰三角形PBC的顶点,且
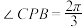 ,求连廊
,求连廊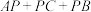 的长(单位为百米);
的长(单位为百米);(2)若分别在AB,BC,CA上取点D,E,F,并建造连廊,使得△DEF变成池中池,放养更名贵的鱼类供游客观赏:方案二如图②,使得△DEF为正三角形,设
 为图②中△DEF的面积,求
为图②中△DEF的面积,求 的最小值;方案三如图③,使得DE平行于AB,且EF垂直于DE,设
的最小值;方案三如图③,使得DE平行于AB,且EF垂直于DE,设 为图③中△DEF的面积,求
为图③中△DEF的面积,求 的取值范围.
的取值范围.
您最近一年使用:0次
2022-07-02更新
|
2578次组卷
|
8卷引用:广东省五校(广州市第二中学等)2021-2022学年高一下学期期末联考数学试题
名校
3 . 2020年5月,《东莞市生活垃圾分类三年行动方案》出台.根据该方案,小明家所在小区设置了两个垃圾回收点A,B,他从自家楼下出发,向正北方向走80米,到达回收点A,再向南偏东60°方向走30米,到达回收点B,则他从回收点B回到自家楼下至少还需走( )
| A.50米 | B.57米 | C.64米 | D.70米 |
您最近一年使用:0次
2021-02-16更新
|
509次组卷
|
2卷引用:广东省东莞市2020-2021学年高二上学期期末数学试题
名校
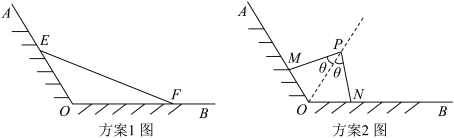
4 . 汕头市有一块如图所示的海岸, ,
, 为岸边,岸边形成
为岸边,岸边形成 角,现拟在此海岸用围网建一个养殖场,现有以下两个方案:
角,现拟在此海岸用围网建一个养殖场,现有以下两个方案:
方案l:在岸边 ,
, 上分别取点
上分别取点 ,
, ,用长度为
,用长度为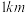 的围网依托岸边围成三角形
的围网依托岸边围成三角形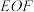 (
( 为围网).
为围网).
方案2:在 的平分线上取一点
的平分线上取一点 ,再从岸边
,再从岸边 ,
, 上分别取点
上分别取点 ,
, ,使得
,使得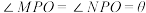 ,用长度为
,用长度为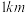 的围网依托岸边围成四边形
的围网依托岸边围成四边形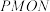 (
( ,
, 为围网).
为围网).
记三角形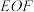 的面积为
的面积为 ,四边形
,四边形 的面积为
的面积为 . 请分别计算
. 请分别计算 ,
, 的最大值,并比较哪个方案好.
的最大值,并比较哪个方案好.
 ,
, 为岸边,岸边形成
为岸边,岸边形成 角,现拟在此海岸用围网建一个养殖场,现有以下两个方案:
角,现拟在此海岸用围网建一个养殖场,现有以下两个方案:方案l:在岸边
 ,
, 上分别取点
上分别取点 ,
, ,用长度为
,用长度为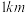 的围网依托岸边围成三角形
的围网依托岸边围成三角形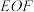 (
( 为围网).
为围网).方案2:在
 的平分线上取一点
的平分线上取一点 ,再从岸边
,再从岸边 ,
, 上分别取点
上分别取点 ,
, ,使得
,使得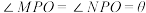 ,用长度为
,用长度为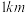 的围网依托岸边围成四边形
的围网依托岸边围成四边形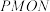 (
( ,
, 为围网).
为围网).记三角形
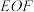 的面积为
的面积为 ,四边形
,四边形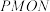 的面积为
的面积为 . 请分别计算
. 请分别计算 ,
, 的最大值,并比较哪个方案好.
的最大值,并比较哪个方案好.
您最近一年使用:0次
2019-12-26更新
|
599次组卷
|
3卷引用:广东省汕头市金山中学2018-2019学年高三上学期期末数学(文)试题
广东省汕头市金山中学2018-2019学年高三上学期期末数学(文)试题广东省汕头市金山中学2020-2021学年高二上学期期末数学试题(已下线)专题03 三角函数中的实际应用问题(第一篇)-备战2020年高考数学大题精做之解答题题型全覆盖
名校
5 . 在数学建模课上,老师给大家带来了一则新闻:“2019年8月16日上午,423米的东莞第一高楼民盈国贸中心2号楼(以下简称“国贸中心”)正式封顶,随着最后一方混凝土浇筑到位,标志着东莞最高楼纪录诞生,由东莞本地航母级企业民盈集团刷新了东莞天际线,比之前的东莞第一高楼台商大厦高出134米.”在同学们的惊叹中,老师提出了问题:国贸中心真有这么高吗?我们能否运用所学知识测量验证一下?一周后,两个兴趣小组分享了他们各自的测量方案.
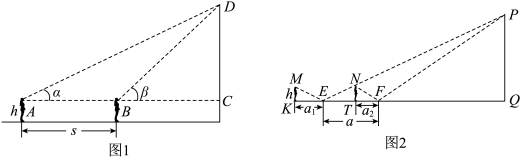
第一小组采用的是“两次测角法”:他们在国贸中心隔壁的会展中心广场上的 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为 ,正对国贸中心前进了
,正对国贸中心前进了 米后,到达
米后,到达 点,在
点,在 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为 ,然后计算出国贸中心的高度(如图).
,然后计算出国贸中心的高度(如图).
第二小组采用的是“镜面反射法”:在国贸中心后面的新世纪豪园一幢11层楼(与国贸中心处于同一水平面,每层约3米)楼顶天台上,进行两个操作步骤:①将平面镜置于天台地面上,人后退至从镜中能看到国贸大厦的顶部位置,测量出人与镜子的距离为 米;②正对国贸中心,将镜子前移
米;②正对国贸中心,将镜子前移 米,重复①中的操作,测量出人与镜子的距离为
米,重复①中的操作,测量出人与镜子的距离为 米.然后计算出国贸中心的高度(如图).
米.然后计算出国贸中心的高度(如图).
实际操作中,第一小组测得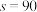 米,
米,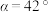 ,
,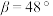 ,最终算得国贸中心高度为
,最终算得国贸中心高度为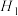 ;第二小组测得
;第二小组测得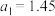 米,
米,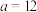 米,
米, 米,最终算得国贸中心高度为
米,最终算得国贸中心高度为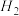 ;假设他们测量者的“眼高
;假设他们测量者的“眼高 ”都为
”都为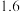 米.
米.
(1)请你用所学知识帮两个小组完成计算(参考数据: ,
, ,答案保留整数结果);
,答案保留整数结果);
(2)你认为哪个小组的方案更好,说出你的理由.
第一小组采用的是“两次测角法”:他们在国贸中心隔壁的会展中心广场上的
 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为 ,正对国贸中心前进了
,正对国贸中心前进了 米后,到达
米后,到达 点,在
点,在 点测得国贸中心顶部的仰角为
点测得国贸中心顶部的仰角为 ,然后计算出国贸中心的高度(如图).
,然后计算出国贸中心的高度(如图).第二小组采用的是“镜面反射法”:在国贸中心后面的新世纪豪园一幢11层楼(与国贸中心处于同一水平面,每层约3米)楼顶天台上,进行两个操作步骤:①将平面镜置于天台地面上,人后退至从镜中能看到国贸大厦的顶部位置,测量出人与镜子的距离为
 米;②正对国贸中心,将镜子前移
米;②正对国贸中心,将镜子前移 米,重复①中的操作,测量出人与镜子的距离为
米,重复①中的操作,测量出人与镜子的距离为 米.然后计算出国贸中心的高度(如图).
米.然后计算出国贸中心的高度(如图).实际操作中,第一小组测得
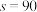 米,
米,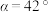 ,
,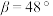 ,最终算得国贸中心高度为
,最终算得国贸中心高度为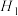 ;第二小组测得
;第二小组测得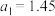 米,
米,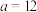 米,
米, 米,最终算得国贸中心高度为
米,最终算得国贸中心高度为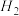 ;假设他们测量者的“眼高
;假设他们测量者的“眼高 ”都为
”都为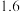 米.
米.
(1)请你用所学知识帮两个小组完成计算(参考数据:
 ,
, ,答案保留整数结果);
,答案保留整数结果);(2)你认为哪个小组的方案更好,说出你的理由.
您最近一年使用:0次
2020-01-23更新
|
367次组卷
|
3卷引用:广东省东莞市2019-2020学年高二上学期期末数学试题
广东省东莞市2019-2020学年高二上学期期末数学试题陕西省西安中学2019-2020学年高二上学期期末教学质量检查数学试题(已下线)【新教材精创】9.2正弦定理与余弦定理的应用(第1课时)练习(1)
11-12高三上·安徽六安·期中
名校
6 . 如图,现有一块半径为2m,圆心角为 的扇形铁皮
的扇形铁皮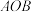 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形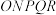 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形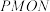 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形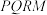 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形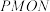 的面积达到最大,在此前提下,再使直角梯形
的面积达到最大,在此前提下,再使直角梯形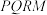 的面积也达到最大.
的面积也达到最大.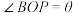 ,当矩形
,当矩形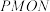 的面积最大时,求
的面积最大时,求 的值;
的值;
(2)求按这种裁剪方法的原材料利用率.
 的扇形铁皮
的扇形铁皮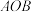 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形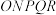 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形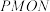 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形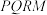 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形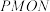 的面积达到最大,在此前提下,再使直角梯形
的面积达到最大,在此前提下,再使直角梯形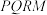 的面积也达到最大.
的面积也达到最大.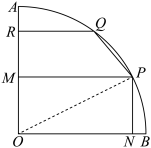
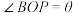 ,当矩形
,当矩形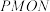 的面积最大时,求
的面积最大时,求 的值;
的值;(2)求按这种裁剪方法的原材料利用率.
您最近一年使用:0次
2016-12-01更新
|
1085次组卷
|
4卷引用:广东省汕头市金山中学2020-2021学年高一上学期期末数学试题
广东省汕头市金山中学2020-2021学年高一上学期期末数学试题(已下线)2012届安徽省舒城中学高三第一学期期中考试理科数学河南省郑州市外国语中学2017-2018学年高一下学期期中数学试题山东省临沂第十八中学2023-2024学年高一下学期3月阶段性测试数学试题



