1 . 设 为实数,定义
为实数,定义 生成数列
生成数列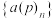 和其特征数列
和其特征数列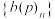 如下:
如下:
(i)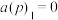 ;
;
(ii)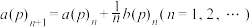 ,其中
,其中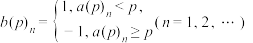 .
.
(1)直接写出 生成数列的前4项;
生成数列的前4项;
(2)判断以下三个命题的真假并说明理由;
①对任意实数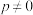 ,都有
,都有 ;
;
②对任意实数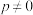 ,都有
,都有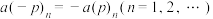 ;
;
③存在自然数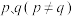 和正整数
和正整数 ,对任意自然数
,对任意自然数 ,有
,有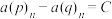 ,其中
,其中 为常数.
为常数.
(3)从一个无穷数列中抽出无穷多项,依原来的顺序组成一个新的无穷数列,若新数列是递增数列,则称之为原数列的一个无穷递增子列.求证:对任意正实数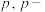 生成数列
生成数列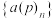 存在无穷递增子列.
存在无穷递增子列.
 为实数,定义
为实数,定义 生成数列
生成数列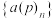 和其特征数列
和其特征数列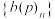 如下:
如下:(i)
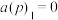 ;
;(ii)
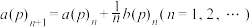 ,其中
,其中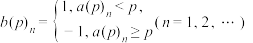 .
.(1)直接写出
 生成数列的前4项;
生成数列的前4项;(2)判断以下三个命题的真假并说明理由;
①对任意实数
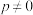 ,都有
,都有 ;
;②对任意实数
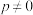 ,都有
,都有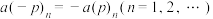 ;
;③存在自然数
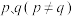 和正整数
和正整数 ,对任意自然数
,对任意自然数 ,有
,有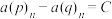 ,其中
,其中 为常数.
为常数.(3)从一个无穷数列中抽出无穷多项,依原来的顺序组成一个新的无穷数列,若新数列是递增数列,则称之为原数列的一个无穷递增子列.求证:对任意正实数
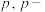 生成数列
生成数列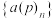 存在无穷递增子列.
存在无穷递增子列.
您最近一年使用:0次
名校
解题方法
2 . 关于 的函数
的函数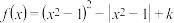 ,给出下列四个命题,其中是真命题的为( ).
,给出下列四个命题,其中是真命题的为( ).
 的函数
的函数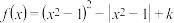 ,给出下列四个命题,其中是真命题的为( ).
,给出下列四个命题,其中是真命题的为( ).A.存在实数 ,使得函数恰有2个零点; ,使得函数恰有2个零点; |
B.存在实数 ,使得函数恰有4个零点; ,使得函数恰有4个零点; |
C.存在实数 ,使得函数恰有5个零点; ,使得函数恰有5个零点; |
D.存在实数 ,使得函数恰有8个零点; ,使得函数恰有8个零点; |
您最近一年使用:0次
2021-08-27更新
|
1314次组卷
|
6卷引用:专题14 导数法妙解函数零点、方程根的问题-备战2022年高考数学一轮复习一网打尽之重点难点突破
(已下线)专题14 导数法妙解函数零点、方程根的问题-备战2022年高考数学一轮复习一网打尽之重点难点突破(已下线)专题2-3 零点-2022年高考数学毕业班二轮热点题型归纳与变式演练(全国通用)福建省晋江市子江中学2019-2020学年高二下学期期末考试数学试题江苏省南通、盐城 、淮安、 宿迁等地部分学校2021-2022学年高一上学期第一次大联考数学试题湖南省岳阳市岳阳县第一中学、汨罗市第一中学2021-2022学年高一上学期期中联考数学试题(已下线)第四章 导数与函数的零点 专题二 定量问题 微点2 函数零点个数问题综合训练
名校
3 . 下列选项中,说法正确的是( )
A.命题“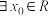 , ,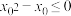 ”的否定为“ ”的否定为“ , ,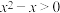 ” ” |
B.命题“在 中, 中,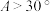 ,则 ,则 ”的逆否命题为真命题 ”的逆否命题为真命题 |
C.若非零向量 、 、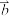 满足 满足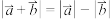 ,则 ,则 与 与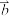 共线 共线 |
D.设 是公比为 是公比为 的等比数列,则“ 的等比数列,则“ ”是“ ”是“ 为递增数列”的充分必要条件 为递增数列”的充分必要条件 |
您最近一年使用:0次
2018-10-18更新
|
1847次组卷
|
4卷引用:专题1-2 简易逻辑题型归类-2



