名校
1 . 函数 的单调递减区间是( )
的单调递减区间是( )
 的单调递减区间是( )
的单调递减区间是( )A. | B. | C.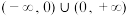 | D. |
您最近一年使用:0次
2022-04-09更新
|
3345次组卷
|
15卷引用:云南省丽江市玉龙县第一中学2019-2020学年高一上学期期中数学试题
云南省丽江市玉龙县第一中学2019-2020学年高一上学期期中数学试题江苏省连云港市东海县2019-2020学年高一上学期期中数学试题(已下线)5.3.1 函数的单调性(练习)-2020-2021学年上学期高一数学同步精品课堂(新教材苏教版必修第一册)(已下线)3.2.1 单调性与最大(小)值(精讲)-2021-2022学年高一数学一隅三反系列(人教A版2019必修第一册)(已下线)3.2.1.1 函数的单调性-2021-2022学年高一数学考点讲解练(人教A版2019必修第一册)福建省德化第一中学2021-2022学年高一上学期第一次月考数学试题(已下线)第14讲 函数的单调性-【暑假自学课】2022年新高一数学暑假精品课(苏教版2019必修第一册)(已下线)3.1.2 函数的单调性(1)(已下线)专题19 函数的基本性质 (1)(已下线)第三章 函数的概念与性质专题(2)河北省唐山英才国际学校2022-2023学年高一上学期11月月考数学试题(已下线)5.3 函数的单调性-2022-2023学年高一数学《基础·重点·难点 》全面题型高分突破(苏教版2019必修第一册)安徽省合肥市第十中学2021-2022学年高二下学期学考模拟数学试题(已下线)第13讲 函数的单调性9种常见题型(1)-【同步题型讲义】(人教A版2019必修第一册)吉林省白山市第七中学2023-2024学年高一上学期11月月考数学试题
20-21高一·江苏·课后作业
名校
2 . 函数 的单调增区间为
的单调增区间为___________ .
 的单调增区间为
的单调增区间为
您最近一年使用:0次
2021-01-07更新
|
2604次组卷
|
7卷引用:8.2+函数与数学模型(重点练)-2020-2021学年高一数学十分钟同步课堂专练(苏教版2019必修第一册)
(已下线)8.2+函数与数学模型(重点练)-2020-2021学年高一数学十分钟同步课堂专练(苏教版2019必修第一册)(已下线)押第11题初等函数-备战2021年高考数学临考题号押题(浙江专用)山西大学附属中学2021-2022学年高一上学期期中数学试题(已下线)3.2 函数的基本性质-2021-2022学年高一数学上学期同步课堂习题测试(人教A版2019必修第一册)(已下线)8.4 单调性(精练)沪教版(2020) 必修第一册 精准辅导 第5章 5.2(4)函数的单调性(2)(已下线)3.2.1单调性与最大(小)值——课后作业(巩固版)
名校
3 . 下列说法中正确 的有( )
A.函数  的递增区间是 的递增区间是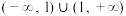 |
B.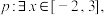 使得 使得 ,若命题 ,若命题 为真命题,则 为真命题,则 |
C.若 对任意实数 对任意实数 都有 都有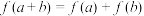 成立,则 成立,则 是奇函数 是奇函数 |
D.已知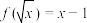 ,则 ,则 的解析式为 的解析式为 |
您最近一年使用:0次
2020-10-31更新
|
726次组卷
|
3卷引用:湖北省荆州中学2020-2021学年高一上学期10月月考数学试题
湖北省荆州中学2020-2021学年高一上学期10月月考数学试题(已下线)考点05+函数的奇偶性-2020-2021学年【补习教材·寒假作业】高一数学(人教B版2019)山西省晋中市榆次区第二中学2023-2024学年高二下学期期末考试数学试题
名校
4 . 已知函数 ,则该函数的单调递减区间为( )
,则该函数的单调递减区间为( )
 ,则该函数的单调递减区间为( )
,则该函数的单调递减区间为( )A.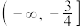 | B.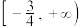 | C.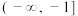 | D. |
您最近一年使用:0次
名校
5 . 函数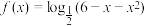 的单调递增区间是
的单调递增区间是________
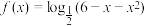 的单调递增区间是
的单调递增区间是
您最近一年使用:0次
2020-07-01更新
|
4026次组卷
|
13卷引用:广东省增城中学2019-2020学年高一上学期期中数学试题
广东省增城中学2019-2020学年高一上学期期中数学试题(已下线)考点13 对数与对数函数(考点专练)-备战2021年新高考数学一轮复习考点微专题江西省上饶市横峰中学2021届高三上学期第一次月考数学(文)试题天津市南开中学2020-2021学年高三上学期统练3数学试题新疆昌吉州教育共同体2020-2021学年高一上学期期中考试数学试题河南省实验中学2020-2021学年高二下学期期中数学文试题重庆南开中学2021-2022学年高一上学期12月月考数学试题黑龙江省哈尔滨市南岗区实验中学2021-2022学年高三上学期数学(理)第三次月考(开学考)试题(已下线)8.4 单调性(精讲)甘肃省兰州市第六十三中学2022-2023学年高一上学期期中数学试题宁夏银川一中2022-2023学年高二下学期期中考试数学(文)试题安徽省桐城中学2021-2022学年高三上学期第二次月考数学(理)试题重庆市第一中学校2023-2024学年高一上学期12月月考数学试题
名校
6 . 设f(x)=x2(2-x),则f(x)的单调增区间是( )
A.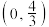 | B. |
| C.(-∞,0) | D.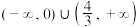 |
您最近一年使用:0次
7 . 函数 的单调递增区间是( )
的单调递增区间是( )
 的单调递增区间是( )
的单调递增区间是( )A. | B. | C. | D. |
您最近一年使用:0次
2020-06-08更新
|
2224次组卷
|
4卷引用:2019年浙江省普通高中学业水平冲A卷(二)
2019年浙江省普通高中学业水平冲A卷(二)衔接点18 函数的单调性与最大(小)值-2020年【衔接教材·暑假作业】初高中衔接数学(人教版)(已下线)3.2.1+单调性与最大(小)值(第二课时)-【新教材】人教A版(2019)高中数学必修第一册导学案陕西省汉中市汉台中学2021-2022学年高三上学期月考(一)文科数学试题
名校
解题方法
8 . 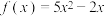 的单调增区间为( )
的单调增区间为( )
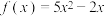 的单调增区间为( )
的单调增区间为( )A.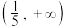 | B.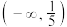 | C.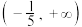 | D.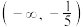 |
您最近一年使用:0次
2020-03-18更新
|
2656次组卷
|
6卷引用:山西省大同市煤矿第四中学2018-2019学年高二下学期3月阶段性测试数学(理)试题
山西省大同市煤矿第四中学2018-2019学年高二下学期3月阶段性测试数学(理)试题2020届新疆阿克苏市阿瓦提四中高三上学期第二次月考理科数学试题(已下线)3.4 函数的单调性(精练)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)第02讲 函数的单调性与最大(小)值 (高频考点-精讲)-1(已下线)专题07 函数的性质-单调性、奇偶性、周期性-1(已下线)第二章 函数的概念与性质 第二节 函数的单调性与最值(核心考点集训)
解题方法
9 . 已知函数 .
.
(1)若函数 的图象过点(2,2),求函数
的图象过点(2,2),求函数
 的单调递增区间;
的单调递增区间;
(2)若函数 是偶函数,求
是偶函数,求 值.
值.
 .
.(1)若函数
 的图象过点(2,2),求函数
的图象过点(2,2),求函数
 的单调递增区间;
的单调递增区间;(2)若函数
 是偶函数,求
是偶函数,求 值.
值.
您最近一年使用:0次
2020-03-11更新
|
1751次组卷
|
2卷引用:湖南省2015年普通高中学业水平考试数学试题
名校
10 . 函数 的单调递增区间为
的单调递增区间为
 的单调递增区间为
的单调递增区间为A.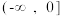 | B.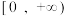 | C. | D. |
您最近一年使用:0次
2019-12-29更新
|
1601次组卷
|
8卷引用:2015-2016学年吉林省延边州汪清六中高二下3月月考文科数学试卷
2015-2016学年吉林省延边州汪清六中高二下3月月考文科数学试卷黑龙江省绥化市青冈县第一中学2019-2020学年高一上学期(A班)期中数学试题山东省潍坊市诸城市2019-2020学年高一上学期期末考试数学试题衔接点18 函数的单调性与最大(小)值-2020年【衔接教材·暑假作业】初高中衔接数学(人教版)(已下线)第05讲-函数的单调性与最值-2021年新高考数学一轮专题复习(新高考专版)西藏林芝市第二高级中学2019-2020学年高二下学期第一学段考试(期中)数学(文)试题(已下线)3.2 函数的性质(精练)-2020-2021学年一隅三反系列之高一数学新教材必修第一册(人教版A版)吉林省长春市第二十九中学2020-2021学年高二下学期期中数学(文)试题



