解题方法
1 . 对于函数 ,函数图象上任意一点A关于点P的对称点
,函数图象上任意一点A关于点P的对称点 仍在函数图象上,那么称点P为函数图象的对称中心.如果
仍在函数图象上,那么称点P为函数图象的对称中心.如果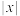 足够大时,图象上的点到直线
足够大时,图象上的点到直线 的距离比任意给定的正数还要小,那么称函数图象无限趋近于该直线
的距离比任意给定的正数还要小,那么称函数图象无限趋近于该直线 ,也称直线
,也称直线 是函数图象的非垂直渐近线.
是函数图象的非垂直渐近线.
(1)研究函数 的性质,填表但无需过程:
的性质,填表但无需过程:
(2)根据(1),在所给的坐标系中,画出大致图象,如有对称中心,则在图象中标为点P,如有非垂直渐近线,用虚线画出;
①如果函数 的图象有对称中心,请根据题设的定义来证明,如果没有,请说明理由;
的图象有对称中心,请根据题设的定义来证明,如果没有,请说明理由;
②请根据题设的定义,证明:函数 的图象在x轴上方,且无限趋近于x轴,但永不相交.
的图象在x轴上方,且无限趋近于x轴,但永不相交.
 ,函数图象上任意一点A关于点P的对称点
,函数图象上任意一点A关于点P的对称点 仍在函数图象上,那么称点P为函数图象的对称中心.如果
仍在函数图象上,那么称点P为函数图象的对称中心.如果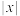 足够大时,图象上的点到直线
足够大时,图象上的点到直线 的距离比任意给定的正数还要小,那么称函数图象无限趋近于该直线
的距离比任意给定的正数还要小,那么称函数图象无限趋近于该直线 ,也称直线
,也称直线 是函数图象的非垂直渐近线.
是函数图象的非垂直渐近线.(1)研究函数
 的性质,填表但无需过程:
的性质,填表但无需过程:| 值域 | |
| 单调性 | |
| 奇偶性 | |
| 图象对称中心 | |
| 图象非垂直渐近线 |
(2)根据(1),在所给的坐标系中,画出大致图象,如有对称中心,则在图象中标为点P,如有非垂直渐近线,用虚线画出;

①如果函数
 的图象有对称中心,请根据题设的定义来证明,如果没有,请说明理由;
的图象有对称中心,请根据题设的定义来证明,如果没有,请说明理由;②请根据题设的定义,证明:函数
 的图象在x轴上方,且无限趋近于x轴,但永不相交.
的图象在x轴上方,且无限趋近于x轴,但永不相交.
您最近一年使用:0次
解题方法
2 . (1)在同一个直角坐标系中画出下列 个函数在区间
个函数在区间 上的图象:
上的图象: ,
, ,
,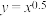 ,
,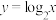 .
.
结合这 个函数的图象,比较它们随着
个函数的图象,比较它们随着 的增大函数值增长的快慢,并指出:当
的增大函数值增长的快慢,并指出:当 的值足够大(
的值足够大(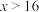 )的时候,这
)的时候,这 个函数的值的大小关系;
个函数的值的大小关系;
(2)先想象下列两组函数图象之间的关系,再用数值验算,提出更一般的猜想.
①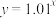 与
与 ;②
;②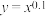 与
与 .
.
(3)借助图形计算器或计算机,作出下列两组函数的图象,验证你在(2)中的猜想.
① 与
与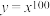 ;②
;②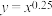 与
与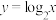 .
.
 个函数在区间
个函数在区间 上的图象:
上的图象: ,
, ,
,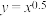 ,
,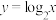 .
.结合这
 个函数的图象,比较它们随着
个函数的图象,比较它们随着 的增大函数值增长的快慢,并指出:当
的增大函数值增长的快慢,并指出:当 的值足够大(
的值足够大(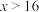 )的时候,这
)的时候,这 个函数的值的大小关系;
个函数的值的大小关系;(2)先想象下列两组函数图象之间的关系,再用数值验算,提出更一般的猜想.
①
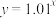 与
与 ;②
;②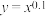 与
与 .
.(3)借助图形计算器或计算机,作出下列两组函数的图象,验证你在(2)中的猜想.
①
 与
与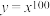 ;②
;②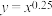 与
与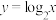 .
.
您最近一年使用:0次



