1 . 人们很早以前就开始探索高次方程的数值求解问题.牛顿在《流数法》一书中给出了牛顿迭代法:用“做切线”的方法求方程的近似解.具体步骤如下:设 是函数
是函数 的一个零点,任意选取
的一个零点,任意选取 作为
作为 的初始近似值,曲线
的初始近似值,曲线 在点
在点 处的切线为
处的切线为 ,设
,设 与
与 轴交点的横坐标为
轴交点的横坐标为 ,并称
,并称 为
为 的1次近似值;曲线
的1次近似值;曲线 在点
在点 处的切线为
处的切线为 ,设
,设 与
与 轴交点的横坐标为
轴交点的横坐标为 ,称
,称 为
为 的2次近似值.一般地,曲线
的2次近似值.一般地,曲线 在点
在点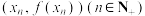 处的切线为
处的切线为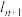 ,记
,记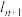 与
与 轴交点的横坐标为
轴交点的横坐标为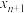 ,并称
,并称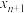 为
为 的
的 次近似值.在一定精确度下,用四舍五入法取值,当
次近似值.在一定精确度下,用四舍五入法取值,当 与
与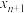 的近似值相等时,该近似值即作为函数
的近似值相等时,该近似值即作为函数 的一个零点
的一个零点 的近似值.下列说法正确的是( )
的近似值.下列说法正确的是( )
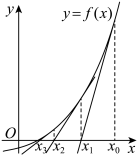
 是函数
是函数 的一个零点,任意选取
的一个零点,任意选取 作为
作为 的初始近似值,曲线
的初始近似值,曲线 在点
在点 处的切线为
处的切线为 ,设
,设 与
与 轴交点的横坐标为
轴交点的横坐标为 ,并称
,并称 为
为 的1次近似值;曲线
的1次近似值;曲线 在点
在点 处的切线为
处的切线为 ,设
,设 与
与 轴交点的横坐标为
轴交点的横坐标为 ,称
,称 为
为 的2次近似值.一般地,曲线
的2次近似值.一般地,曲线 在点
在点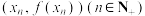 处的切线为
处的切线为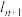 ,记
,记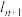 与
与 轴交点的横坐标为
轴交点的横坐标为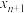 ,并称
,并称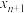 为
为 的
的 次近似值.在一定精确度下,用四舍五入法取值,当
次近似值.在一定精确度下,用四舍五入法取值,当 与
与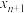 的近似值相等时,该近似值即作为函数
的近似值相等时,该近似值即作为函数 的一个零点
的一个零点 的近似值.下列说法正确的是( )
的近似值.下列说法正确的是( )
A.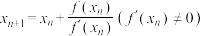 |
B.利用牛顿迭代法求函数 的零点 的零点 的近似值(精确到0.1),取 的近似值(精确到0.1),取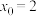 ,需要做两条切线即可确定 ,需要做两条切线即可确定 的近似值 的近似值 |
C.利用二分法求函数 的零点 的零点 的近似值(精确度为0.1),给定初始区间为 的近似值(精确度为0.1),给定初始区间为 ,需进行4次区间二分可得到零点 ,需进行4次区间二分可得到零点 的近似值 的近似值 |
D.利用牛顿迭代法求函数 的零点 的零点 的近似值,任取 的近似值,任取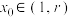 ,总有 ,总有 |
您最近半年使用:0次



