名校
1 . 下列命题中正确的是( )
| A.四棱柱、四棱台、五棱锥都是六面体 |
| B.侧面是全等的等腰三角形的棱锥是正棱锥 |
C.在 中,若 中,若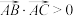 ,则 ,则 为锐角三角形 为锐角三角形 |
| D.长方体的长宽高分别为3、2、1,该长方体的外接球表面积为14π |
您最近一年使用:0次
名校
2 . 十八世纪,数学家欧拉发现简单凸多面体的顶点数V、棱数E及面数F之间有固定的关系,即著名的欧拉公式: .如图所示为上世纪八十年代科学家首次发现的碳60的电子显微镜图,它是由五边形和六边形面构成的多面体,共有60个顶点,每个顶点均为碳原子,且每个顶点引出三条棱,形似足球.根据以上信息知,碳60的所有面中五边形的个数是( )
.如图所示为上世纪八十年代科学家首次发现的碳60的电子显微镜图,它是由五边形和六边形面构成的多面体,共有60个顶点,每个顶点均为碳原子,且每个顶点引出三条棱,形似足球.根据以上信息知,碳60的所有面中五边形的个数是( )
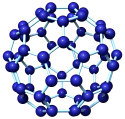
 .如图所示为上世纪八十年代科学家首次发现的碳60的电子显微镜图,它是由五边形和六边形面构成的多面体,共有60个顶点,每个顶点均为碳原子,且每个顶点引出三条棱,形似足球.根据以上信息知,碳60的所有面中五边形的个数是( )
.如图所示为上世纪八十年代科学家首次发现的碳60的电子显微镜图,它是由五边形和六边形面构成的多面体,共有60个顶点,每个顶点均为碳原子,且每个顶点引出三条棱,形似足球.根据以上信息知,碳60的所有面中五边形的个数是( )
| A.12 | B.20 | C.32 | D.40 |
您最近一年使用:0次
2022-03-23更新
|
777次组卷
|
2卷引用:重庆市2022届高三高考模拟调研(三)数学试题
3 . 山西五台山佛光寺大殿是庑殿顶建筑的典型代表.庑殿顶四面斜坡,有一条正脊和四条斜脊,又叫五脊殿.《九章算术》把这种底面为矩形,顶部为一条棱的五面体叫做“刍甍”,并给出了其体积公式: ×(2×下袤+上袤)×广×高(广:东西方向长度;袤:南北方向长度).已知一刍甍状庑殿顶,南北长18m,东西长8m,正脊长12m,斜脊长
×(2×下袤+上袤)×广×高(广:东西方向长度;袤:南北方向长度).已知一刍甍状庑殿顶,南北长18m,东西长8m,正脊长12m,斜脊长 m,则其体积为( ).
m,则其体积为( ).

 ×(2×下袤+上袤)×广×高(广:东西方向长度;袤:南北方向长度).已知一刍甍状庑殿顶,南北长18m,东西长8m,正脊长12m,斜脊长
×(2×下袤+上袤)×广×高(广:东西方向长度;袤:南北方向长度).已知一刍甍状庑殿顶,南北长18m,东西长8m,正脊长12m,斜脊长 m,则其体积为( ).
m,则其体积为( ).
A.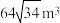 | B.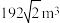 | C.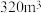 | D.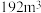 |
您最近一年使用:0次
2022-03-05更新
|
1060次组卷
|
5卷引用:重庆市缙云教育联盟2021-2022学年高一下学期6月质量检测数学试题
4 . 如图甲是一水晶饰品,名字叫梅尔卡巴,其对应的几何体叫星形八面体,也叫八角星体,是一种二复合四面体,它是由两个有共同中心的正四面体交叉组合而成,且所有面都是全等的小正三角形,如图乙所示.若一星形八面体中两个正四面体的棱长均为2,则该星形八面体的体积为______ .


您最近一年使用:0次
2021-06-03更新
|
947次组卷
|
6卷引用:重庆市第八中学2021届高三下学期模拟(八)数学试题
重庆市第八中学2021届高三下学期模拟(八)数学试题云南省文山壮族苗族自治州第一中学2020-2021学年高一下学期期末数学试题(已下线)7.3 空间几何体积及表面积(精练)-【一隅三反】2022年高考数学一轮复习(新高考地区专用)(已下线)专题34 立体几何解答题中的体积求解策略-学会解题之高三数学万能解题模板【2022版】(已下线)专题24 空间几何体的表面积与体积-2(已下线)第二章 立体几何中的计算 专题三 空间体积的计算 微点7 空间图形体积的计算综合训练【培优版】



