名校
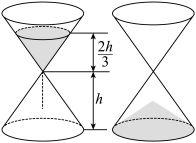
1 . 中国古代计时器的发明时间不晚于战国时代(公元前476年~前222年),其中沙漏就是古代利用机械原理设计的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道流到下部容器,如图,某沙漏由上、下两个圆锥容器组成,圆锥的底面圆的直径和高均为8 cm,细沙全部在上部时,其高度为圆锥高度的 (细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
(细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
 (细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
(细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
| A.2 cm | B.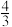 cm cm | C. cm cm | D.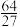 cm cm |
您最近一年使用:0次
2019-12-16更新
|
748次组卷
|
9卷引用:福建省龙岩市龙岩第一中学2019-2020学年高三上学期期中数学(文)试题
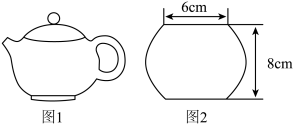
2 . 西施壶是紫砂壶器众多款式中最经典的壶型之一,是一款非常实用的泡茶工具(如图1).西施壶的壶身可近似看成一个球体截去上下两个相同的球缺的几何体.球缺的体积 (R为球缺所在球的半径,h为球缺的高).若一个西施壶的壶身高为8cm,壶口直径为6cm(如图2),则该壶壶身的容积约为(不考虑壶壁厚度,π取3.14)( )
(R为球缺所在球的半径,h为球缺的高).若一个西施壶的壶身高为8cm,壶口直径为6cm(如图2),则该壶壶身的容积约为(不考虑壶壁厚度,π取3.14)( )
 (R为球缺所在球的半径,h为球缺的高).若一个西施壶的壶身高为8cm,壶口直径为6cm(如图2),则该壶壶身的容积约为(不考虑壶壁厚度,π取3.14)( )
(R为球缺所在球的半径,h为球缺的高).若一个西施壶的壶身高为8cm,壶口直径为6cm(如图2),则该壶壶身的容积约为(不考虑壶壁厚度,π取3.14)( )
| A.494ml | B.506ml | C.509ml | D.516ml |
您最近一年使用:0次
2023-03-07更新
|
1992次组卷
|
9卷引用:福建省厦门市2023届高三下学期第二次质量检测数学试题
名校
解题方法
3 . 某同学使用某品牌暖水瓶,其内胆规格如图所示.若水瓶内胆壁厚不计,且内胆如图分为①②③④四个部分,它们分别为一个半球、一个大圆柱、一个圆台和一个小圆柱体.若其中圆台部分的体积为 ,且水瓶灌满水后盖上瓶塞时水溢出
,且水瓶灌满水后盖上瓶塞时水溢出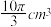 .记盖上瓶塞后,水瓶的最大盛水量为
.记盖上瓶塞后,水瓶的最大盛水量为 ,
,
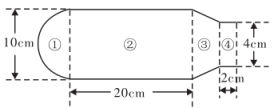
(1)求 ;
;
(2)该同学发现:该品牌暖水瓶盛不同体积的热水时,保温效果不同.为了研究保温效果最好时暖水瓶的盛水体积,做以下实验:把盛有最大盛水量 的水的暖水瓶倒出不同体积的水,并记录水瓶内不同体积水在不同时刻的水温,发现水温
的水的暖水瓶倒出不同体积的水,并记录水瓶内不同体积水在不同时刻的水温,发现水温 (单位:℃)与时刻
(单位:℃)与时刻 满足线性回归方程
满足线性回归方程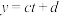 ,通过计算得到下表:
,通过计算得到下表:
注:表中倒出体积 (单位:
(单位: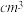 )是指从最大盛水量中倒出的那部分水的体积.其中:
)是指从最大盛水量中倒出的那部分水的体积.其中:
令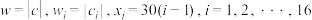 .对于数据
.对于数据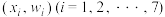 ,可求得回归直线为
,可求得回归直线为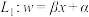 ,对于数据
,对于数据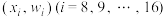 ,可求得回归直线为
,可求得回归直线为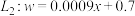 .
.
(ⅰ)指出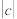 的实际意义,并求出回归直线
的实际意义,并求出回归直线 的方程(参考数据:
的方程(参考数据: );
);
(ⅱ)若 与
与 的交点横坐标即为最佳倒出体积,请问保温瓶约盛多少体积水时(盛水体积保留整数,且
的交点横坐标即为最佳倒出体积,请问保温瓶约盛多少体积水时(盛水体积保留整数,且 取3.14)保温效果最佳?
取3.14)保温效果最佳?
附:对于一组数据 ,其回归直线
,其回归直线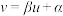 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为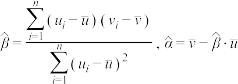 .
.
 ,且水瓶灌满水后盖上瓶塞时水溢出
,且水瓶灌满水后盖上瓶塞时水溢出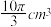 .记盖上瓶塞后,水瓶的最大盛水量为
.记盖上瓶塞后,水瓶的最大盛水量为 ,
,
(1)求
 ;
;(2)该同学发现:该品牌暖水瓶盛不同体积的热水时,保温效果不同.为了研究保温效果最好时暖水瓶的盛水体积,做以下实验:把盛有最大盛水量
 的水的暖水瓶倒出不同体积的水,并记录水瓶内不同体积水在不同时刻的水温,发现水温
的水的暖水瓶倒出不同体积的水,并记录水瓶内不同体积水在不同时刻的水温,发现水温 (单位:℃)与时刻
(单位:℃)与时刻 满足线性回归方程
满足线性回归方程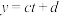 ,通过计算得到下表:
,通过计算得到下表:倒出体积 | 0 | 30 | 60 | 90 | 120 |
| 拟合结果 | 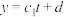 | 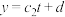 |  | 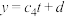 | 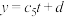 |
倒出体积 | 150 | 180 | 210 | … | 450 |
| 拟合结果 | 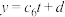 |  | 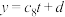 | … |  |
注:表中倒出体积
 (单位:
(单位: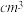 )是指从最大盛水量中倒出的那部分水的体积.其中:
)是指从最大盛水量中倒出的那部分水的体积.其中: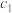 |  | 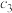 |  | 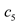 | 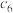 |  |
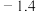 | 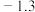 |  |  |  | 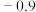 | 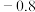 |
令
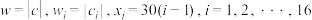 .对于数据
.对于数据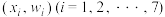 ,可求得回归直线为
,可求得回归直线为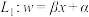 ,对于数据
,对于数据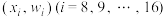 ,可求得回归直线为
,可求得回归直线为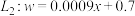 .
.(ⅰ)指出
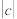 的实际意义,并求出回归直线
的实际意义,并求出回归直线 的方程(参考数据:
的方程(参考数据: );
);(ⅱ)若
 与
与 的交点横坐标即为最佳倒出体积,请问保温瓶约盛多少体积水时(盛水体积保留整数,且
的交点横坐标即为最佳倒出体积,请问保温瓶约盛多少体积水时(盛水体积保留整数,且 取3.14)保温效果最佳?
取3.14)保温效果最佳?附:对于一组数据
 ,其回归直线
,其回归直线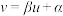 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为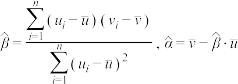 .
.
您最近一年使用:0次
2020-04-23更新
|
453次组卷
|
5卷引用:福建省漳州市南平市2019-2020学年高三第二次教学质量检测理科数学试题



