名校
1 . 古希腊几何学家阿波罗尼斯证明过这样一个命题:平面内到两定点距离之比为常数 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点A,B的距离为2,动点Р满足
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点A,B的距离为2,动点Р满足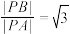 ,若点Р不在直线AB上,则
,若点Р不在直线AB上,则 面积的最大值为( )
面积的最大值为( )
 的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点A,B的距离为2,动点Р满足
的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点A,B的距离为2,动点Р满足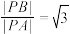 ,若点Р不在直线AB上,则
,若点Р不在直线AB上,则 面积的最大值为( )
面积的最大值为( )| A.1 | B. | C.2 | D. |
您最近一年使用:0次
2022-11-19更新
|
655次组卷
|
10卷引用:安徽省六安市皖西中学2021-2022学年高二上学期期末数学试题
安徽省六安市皖西中学2021-2022学年高二上学期期末数学试题江苏省徐州市睢宁县第一中学2022-2023学年高二上学期10月月考数学试题湖北省武汉市七校2022-2023学年高二上学期期中联考数学试题河南省洛阳市宜阳县第一高级中学2022-2023学年高二上学期第四次月考数学文科试题河南省洛阳市宜阳县第一高级中学2022-2023学年高二上学期清北园第4次能力达标文科数学试题河南省洛阳市宜阳县第一高级中学2022-2023学年高二上学期清北园第四次能力达标检测理科数学试题江苏省南京市建邺高中2022-2023学年高二上学期10月月考数学试题江苏省徐州市鼓楼区求实高中2022-2023学年高二上学期12月期中测试数学试题江苏省南京市建邺高级中学2023-2024学年高二上学期10月月考数学试题河北省秦皇岛市青龙满族自治县实验中学2023-2024学年高二上学期10月月考数学试题
名校
解题方法
2 . 古希腊数学家阿波罗尼斯的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数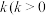 且
且 的点的轨迹是圆,后人将之称为阿波罗尼斯圆.现有椭圆
的点的轨迹是圆,后人将之称为阿波罗尼斯圆.现有椭圆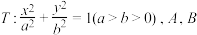 为椭圆
为椭圆 长轴的端点,
长轴的端点, 为椭圆
为椭圆 短轴的端点,
短轴的端点, ,
, 分别为椭圆
分别为椭圆 的左右焦点,动点
的左右焦点,动点 满足
满足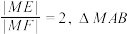 面积的最大值为
面积的最大值为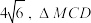 面积的最小值为
面积的最小值为 ,则椭圆
,则椭圆 的离心率为( )
的离心率为( )
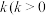 且
且 的点的轨迹是圆,后人将之称为阿波罗尼斯圆.现有椭圆
的点的轨迹是圆,后人将之称为阿波罗尼斯圆.现有椭圆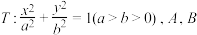 为椭圆
为椭圆 长轴的端点,
长轴的端点, 为椭圆
为椭圆 短轴的端点,
短轴的端点, ,
, 分别为椭圆
分别为椭圆 的左右焦点,动点
的左右焦点,动点 满足
满足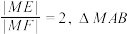 面积的最大值为
面积的最大值为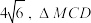 面积的最小值为
面积的最小值为 ,则椭圆
,则椭圆 的离心率为( )
的离心率为( )A. | B. | C. | D. |
您最近一年使用:0次
2022-02-25更新
|
2593次组卷
|
8卷引用:湖北省荆州市八县市2021-2022学年高二上学期期末质量检测数学试题
湖北省荆州市八县市2021-2022学年高二上学期期末质量检测数学试题(已下线)综合测试卷(巅峰版)-【新教材优创】突破满分数学之2022-2023学年高二数学重难点突破+课时训练 (人教A版2019选择性必修第一册)河南省新蔡县第一高级中学2021-2022学年高二下学期3月半月考数学(文科)试题(已下线)技巧05 第二篇 解题技巧(测试卷)--第二篇 解题技巧篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题12 阿波罗尼斯(已下线)专题1 阿波罗尼斯圆及其应用 微点4 阿波罗尼斯圆与圆锥曲线(已下线)第五篇 向量与几何 专题1 蒙日圆与阿氏圆 微点7 阿波罗尼斯圆与圆锥曲线(已下线)专题3 阿波罗尼斯圆及其应用【练】(压轴小题大全)
2021高二·江苏·专题练习
名校
3 . 阿波罗尼斯 约公元前
约公元前 年
年 证明过这样一个命题:平面内到两定点距离之比为常数
证明过这样一个命题:平面内到两定点距离之比为常数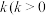 且
且 的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A,B间的距离为2,动点P与A,B距离之比满足:
的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A,B间的距离为2,动点P与A,B距离之比满足: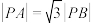 ,当P、A、B三点不共线时,
,当P、A、B三点不共线时, 面积的最大值是( )
面积的最大值是( )
 约公元前
约公元前 年
年 证明过这样一个命题:平面内到两定点距离之比为常数
证明过这样一个命题:平面内到两定点距离之比为常数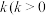 且
且 的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A,B间的距离为2,动点P与A,B距离之比满足:
的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A,B间的距离为2,动点P与A,B距离之比满足: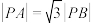 ,当P、A、B三点不共线时,
,当P、A、B三点不共线时, 面积的最大值是( )
面积的最大值是( )A. | B.2 | C. | D. |
您最近一年使用:0次
2022-01-04更新
|
1354次组卷
|
9卷引用:江西省六校2021-2022学年高二上学期期末联考数学(文)试题
江西省六校2021-2022学年高二上学期期末联考数学(文)试题北京市第八十中学2022-2023学年高二上学期适应性考试数学试题(已下线)2.1 圆的方程-2021-2022学年高二数学同步培优训练系列(苏教版2019选择性必修第一册)浙江省北斗联盟2021-2022学年高二下学期期中联考数学试题湖南省衡阳师范学院祁东附属中学2022-2023学年高二上学期期中数学试题(已下线)专题11直线与圆及相关的最值问题(练)--第一篇 热点、难点突破篇-《2022年高考数学二轮复习讲练测(新高考·全国卷)》(已下线)专题26 活用隐圆的五种定义妙解压轴题-2(已下线)专题1 超级名圆 性质优先 练(已下线)技法提升3 正确数形结合,避免解题烦琐或漏解
名校
4 . 阿波罗尼斯(古希腊数学家,约公元前262-190年)的著作《圆锥曲线论》是古代世界光辉的科学成果,它将圆锥曲线的性质网罗殆尽,几乎使后人没有插足的余地.他证明过这样一个命题:平面内与两定点距离的比为常数 (
( 且
且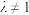 )的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.在平面直角坐标系中,已知
)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.在平面直角坐标系中,已知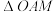 的两个顶点
的两个顶点 是定点,它们的坐标分别为
是定点,它们的坐标分别为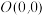 、
、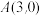 ;另一个顶点
;另一个顶点 是动点,且满足
是动点,且满足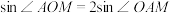 ,则当
,则当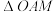 的面积最大时,
的面积最大时, 边上的高为
边上的高为___________ .
 (
( 且
且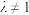 )的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.在平面直角坐标系中,已知
)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.在平面直角坐标系中,已知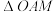 的两个顶点
的两个顶点 是定点,它们的坐标分别为
是定点,它们的坐标分别为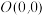 、
、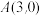 ;另一个顶点
;另一个顶点 是动点,且满足
是动点,且满足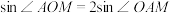 ,则当
,则当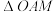 的面积最大时,
的面积最大时, 边上的高为
边上的高为
您最近一年使用:0次
2021-02-04更新
|
1506次组卷
|
3卷引用:四川省巴中中学、南江中学2020-2021学年高二上学期期末联考数学(理)试题
四川省巴中中学、南江中学2020-2021学年高二上学期期末联考数学(理)试题四川省广安市武胜烈面中学校2021-2022学年高二上学期期中测试数学(理)试题(已下线)专题1 阿波罗尼斯圆及其应用 微点6 阿波罗尼斯圆综合训练



