名校
解题方法
1 . 已知椭圆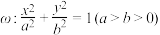 过点
过点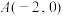 ,且
,且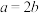 .
.
(1)求椭圆ω的方程;
(2)设O为原点,过点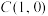 的直线l与椭圆ω交于P,Q两点,且直线l与x轴不重合,直线AP,AQ分别与y轴交于M,N两点.求证
的直线l与椭圆ω交于P,Q两点,且直线l与x轴不重合,直线AP,AQ分别与y轴交于M,N两点.求证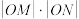 为定值.
为定值.
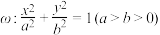 过点
过点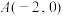 ,且
,且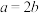 .
.(1)求椭圆ω的方程;
(2)设O为原点,过点
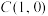 的直线l与椭圆ω交于P,Q两点,且直线l与x轴不重合,直线AP,AQ分别与y轴交于M,N两点.求证
的直线l与椭圆ω交于P,Q两点,且直线l与x轴不重合,直线AP,AQ分别与y轴交于M,N两点.求证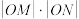 为定值.
为定值.
您最近一年使用:0次
2024-08-14更新
|
1211次组卷
|
12卷引用:新疆吐鲁番市高昌区第二中学2021-2022学年高二上学期期末考试数学(理)试题
新疆吐鲁番市高昌区第二中学2021-2022学年高二上学期期末考试数学(理)试题 北京市丰台区2020-2021学年高二上学期期末练习数学试题北京市中央民族大学附属中学2023-2024学年高二上学期期末复习(四)数学试题(已下线)专练35 综合拔高练-2021-2022学年高二数学上册同步课后专练(人版A版选择性必修第一册)江苏省连云港市2022-2023学年高三上学期期中复习数学试题北京市西城区北京师范大学第二附属中学2023-2024学年高二下学期期中考试数学试题广东省部分学校2025届新高三上学期开学摸底联合教学质量检测(已下线)重难点突破06 弦长问题及长度和、差、商、积问题(七大题型)(已下线)模块二 专题2 解析几何中定值、定点、定直线问题【讲】(高二期中压轴专项)(已下线)专题3 函数思想 确定定值(经典好题母题)【练】广东省揭阳市普宁市华侨中学2024-2025学年高三上学期第一次月考数学试卷(已下线)北京市第一六六中学2024-2025学年高三上学期期中测试数学试卷
名校
解题方法
2 . 已知椭圆 的长轴长为
的长轴长为 ,且点
,且点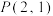 在椭圆
在椭圆 上.
上.
(1)求椭圆 的方程.
的方程.
(2)设 为坐标原点,过点
为坐标原点,过点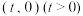 的直线
的直线 (斜率不为0)交椭圆
(斜率不为0)交椭圆 于不同的两点
于不同的两点 (异于点
(异于点 ),直线
),直线 分别与直线
分别与直线 交于
交于 两点,
两点, 的中点为
的中点为 ,是否存在实数
,是否存在实数 ,使直线
,使直线 的斜率为定值?若存在,求出
的斜率为定值?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 的长轴长为
的长轴长为 ,且点
,且点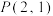 在椭圆
在椭圆 上.
上.(1)求椭圆
 的方程.
的方程.(2)设
 为坐标原点,过点
为坐标原点,过点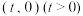 的直线
的直线 (斜率不为0)交椭圆
(斜率不为0)交椭圆 于不同的两点
于不同的两点 (异于点
(异于点 ),直线
),直线 分别与直线
分别与直线 交于
交于 两点,
两点, 的中点为
的中点为 ,是否存在实数
,是否存在实数 ,使直线
,使直线 的斜率为定值?若存在,求出
的斜率为定值?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
您最近一年使用:0次
2023-01-06更新
|
417次组卷
|
3卷引用:新疆乌鲁木齐八一中学2022-2023学年高二上学期期末考试数学试题
解题方法
3 . 已知椭圆 经过点
经过点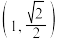 ,且离心率为
,且离心率为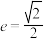 .
.
(1)求椭圆 的方程;
的方程;
(2)已知直线 不过点
不过点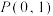 且与椭圆
且与椭圆 交于
交于 、
、 两点,直线
两点,直线 、
、 的斜率分别为
的斜率分别为 、
、 ,则
,则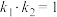 ,证明:直线
,证明:直线 过定点
过定点 .
.
 经过点
经过点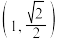 ,且离心率为
,且离心率为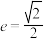 .
.(1)求椭圆
 的方程;
的方程;(2)已知直线
 不过点
不过点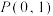 且与椭圆
且与椭圆 交于
交于 、
、 两点,直线
两点,直线 、
、 的斜率分别为
的斜率分别为 、
、 ,则
,则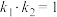 ,证明:直线
,证明:直线 过定点
过定点 .
.
您最近一年使用:0次



