名校
1 . 公元前6世纪,古希腊的毕达哥拉斯学派把 称为黄金数.离心率等于黄金数的倒数的双曲线称为黄金双曲线.若黄金双曲线
称为黄金数.离心率等于黄金数的倒数的双曲线称为黄金双曲线.若黄金双曲线 的左、右顶点分别为
的左、右顶点分别为 ,虚轴的上端点为B,左焦点为F,离心率为e,则( )
,虚轴的上端点为B,左焦点为F,离心率为e,则( )
 称为黄金数.离心率等于黄金数的倒数的双曲线称为黄金双曲线.若黄金双曲线
称为黄金数.离心率等于黄金数的倒数的双曲线称为黄金双曲线.若黄金双曲线 的左、右顶点分别为
的左、右顶点分别为 ,虚轴的上端点为B,左焦点为F,离心率为e,则( )
,虚轴的上端点为B,左焦点为F,离心率为e,则( )| A.a2e=1 | B.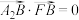 |
| C.顶点到渐近线的距离为e | D.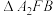 的外接圆的面积为 的外接圆的面积为 |
您最近半年使用:0次
2023-01-15更新
|
1266次组卷
|
8卷引用:福建省福州第三中学2023届高三第十二次质量检测数学试题
福建省福州第三中学2023届高三第十二次质量检测数学试题江苏省苏北四市(徐州、淮安、宿迁、连云港)2022-2023学年高三上学期1月第一次联合调研测试数学试题湖南省娄底市新化县第一中学2022-2023学年高二上学期期末线上测试数学试题江苏省苏北四市(徐州、淮安、宿迁、连云港)2023届高三上学期第一次调研数学试题江苏省南京市金陵中学2022-2023学年高二上学期期末考试数学试题(已下线)模块三 专题2 题型突破篇 小题进阶提升练(2)期末终极研习室(2023-2024学年第一学期)高三(已下线)期末精确押题之多选题(40题)-2023-2024学年高二数学上学期《考点·题型·难点》期末高效复习(人教A版2019)江苏省盐城市射阳中学2023-2024学年高二上学期期末数学试题
名校
解题方法
2 . 公元前 300 年前后, 欧几里得撰写的《几何原本》是最早有关黄金分割的论著, 书中描述: 把一条线段分割为两部分, 使较大部分与全长的比值等于较小部分与较大的比值, 则这个比值即为“黄金分割比”, 把离心率为 “黄金分割比” 倒数的双曲线叫做 “黄金双曲线”. 黄金双曲线 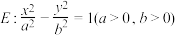 的一个顶点为
的一个顶点为 , 与
, 与 不在
不在 轴同侧的焦点为
轴同侧的焦点为 ,
, 的一个虚轴端点为
的一个虚轴端点为 ,
, 为双曲线任意一条不过原点且斜率存在的弦,
为双曲线任意一条不过原点且斜率存在的弦,  为
为 中点. 设双曲线
中点. 设双曲线 的离心率为
的离心率为 , 则下列说法中, 正确的有( )
, 则下列说法中, 正确的有( )
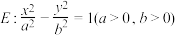 的一个顶点为
的一个顶点为 , 与
, 与 不在
不在 轴同侧的焦点为
轴同侧的焦点为 ,
, 的一个虚轴端点为
的一个虚轴端点为 ,
, 为双曲线任意一条不过原点且斜率存在的弦,
为双曲线任意一条不过原点且斜率存在的弦,  为
为 中点. 设双曲线
中点. 设双曲线 的离心率为
的离心率为 , 则下列说法中, 正确的有( )
, 则下列说法中, 正确的有( )A. | B. |
C.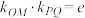 | D.若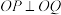 , 则 , 则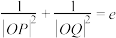 恒成立 恒成立 |
您最近半年使用:0次
2022-09-23更新
|
1833次组卷
|
6卷引用:福建师范大学附属中学2023届高三上学期数学月考试题(三)
名校
解题方法
3 . 瑞士著名数学家欧拉在1765年证明了定理“三角形的外心、重心、垂心依次位于同一条直线上,且重心到外心的距离是重心到垂心距离的一半”,后人称这条直线为“欧拉线”.直线 与
与 轴及双曲线
轴及双曲线 的两条渐近线的三个不同交点构成集合
的两条渐近线的三个不同交点构成集合 ,且
,且 恰为某三角形的外心,重心,垂心所成集合.若
恰为某三角形的外心,重心,垂心所成集合.若 的斜率为1,则该双曲线的离心率可以是( )
的斜率为1,则该双曲线的离心率可以是( )
 与
与 轴及双曲线
轴及双曲线 的两条渐近线的三个不同交点构成集合
的两条渐近线的三个不同交点构成集合 ,且
,且 恰为某三角形的外心,重心,垂心所成集合.若
恰为某三角形的外心,重心,垂心所成集合.若 的斜率为1,则该双曲线的离心率可以是( )
的斜率为1,则该双曲线的离心率可以是( )A.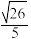 | B.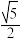 | C. | D.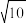 |
您最近半年使用:0次
2021-05-05更新
|
1878次组卷
|
6卷引用:福建省三明市普通高中2021届高三毕业班三模数学试题
福建省三明市普通高中2021届高三毕业班三模数学试题福建省莆田第九中学2023届高三上学期第一次教学质量检测数学模拟试题(已下线)专题27 圆锥曲线与四心问题 微点5 圆锥曲线与四心问题综合训练(已下线)专题28 轻松搞定圆锥曲线离心率十九大模型-5重庆市南开中学校2022-2023学年高二上学期11月月考数学试题(已下线)专题17 圆锥曲线常考压轴小题全归类(16大题型)(练习)



