名校
1 . 已知椭圆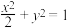 上存在相异两点关于直线
上存在相异两点关于直线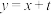 对称,则实数
对称,则实数 的取值范围是
的取值范围是______ .
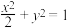 上存在相异两点关于直线
上存在相异两点关于直线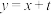 对称,则实数
对称,则实数 的取值范围是
的取值范围是
您最近一年使用:0次
2020-12-11更新
|
697次组卷
|
7卷引用:四川省成都市锦江区成都市盐道街中学2020-2021学年高二上学期期中数学试题
名校
解题方法
2 . 已知抛物线 的焦点与椭圆
的焦点与椭圆 的一个焦点重合,椭圆
的一个焦点重合,椭圆 的左、右顶点分别为
的左、右顶点分别为 ,
, 是椭圆
是椭圆 上一点,记直线
上一点,记直线 的斜率为
的斜率为 、
、 ,且有
,且有 .
.
(1)求椭圆 的方程;
的方程;
(2)若过点 的直线
的直线 与椭圆相交于不同两点
与椭圆相交于不同两点 和
和 ,且满足
,且满足 (
( 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围.
 的焦点与椭圆
的焦点与椭圆 的一个焦点重合,椭圆
的一个焦点重合,椭圆 的左、右顶点分别为
的左、右顶点分别为 ,
, 是椭圆
是椭圆 上一点,记直线
上一点,记直线 的斜率为
的斜率为 、
、 ,且有
,且有 .
.(1)求椭圆
 的方程;
的方程;(2)若过点
 的直线
的直线 与椭圆相交于不同两点
与椭圆相交于不同两点 和
和 ,且满足
,且满足 (
( 为坐标原点),求实数
为坐标原点),求实数 的取值范围.
的取值范围.
您最近一年使用:0次
2020-06-13更新
|
188次组卷
|
2卷引用:四川省攀枝花市第十五中学2019-2020学年高二上学期第一次月考数学文科试题
名校
解题方法
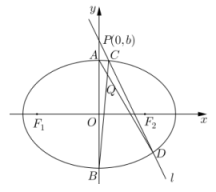
3 . 在平面直角坐标系中,A、B分别为椭圆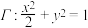 的上、下顶点,若动直线l过点
的上、下顶点,若动直线l过点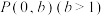 ,且与椭圆
,且与椭圆 相交于C、D两个不同点(直线l与y轴不重合,且C、D两点在y轴右侧,C在D的上方),直线AD与BC相交于点Q.
相交于C、D两个不同点(直线l与y轴不重合,且C、D两点在y轴右侧,C在D的上方),直线AD与BC相交于点Q.
(1)设 的两焦点为
的两焦点为 、
、 ,求
,求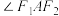 的值;
的值;
(2)若 ,且
,且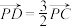 ,求点Q的横坐标;
,求点Q的横坐标;
(3)是否存在这样的点P,使得点Q的纵坐标恒为 ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
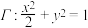 的上、下顶点,若动直线l过点
的上、下顶点,若动直线l过点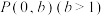 ,且与椭圆
,且与椭圆 相交于C、D两个不同点(直线l与y轴不重合,且C、D两点在y轴右侧,C在D的上方),直线AD与BC相交于点Q.
相交于C、D两个不同点(直线l与y轴不重合,且C、D两点在y轴右侧,C在D的上方),直线AD与BC相交于点Q.
(1)设
 的两焦点为
的两焦点为 、
、 ,求
,求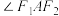 的值;
的值;(2)若
 ,且
,且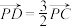 ,求点Q的横坐标;
,求点Q的横坐标;(3)是否存在这样的点P,使得点Q的纵坐标恒为
 ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
您最近一年使用:0次
2020-05-21更新
|
652次组卷
|
5卷引用:2020届上海市闵行区高三二模数学试题
2020届上海市闵行区高三二模数学试题(已下线)热点04 平面向量、复数-2021年高考数学【热点·重点·难点】专练(上海专用)四川省攀枝花市第七高级中学校2021-2022学年高二上学期半期检测数学(理)试题上海市大同中学2022届高三下学期开学考试数学试题(已下线)第13讲 椭圆 - 1
名校
4 . 已知圆 的方程为
的方程为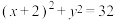 ,点
,点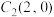 ,点M为圆
,点M为圆 上的任意一点,线段
上的任意一点,线段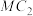 的垂直平分线与线段
的垂直平分线与线段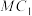 相交于点N.
相交于点N.
(1)求点N的轨迹C的方程.
(2)已知点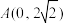 ,过点A且斜率为k的直线
,过点A且斜率为k的直线 交轨迹C于
交轨迹C于 两点,以
两点,以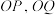 为邻边作平行四边形
为邻边作平行四边形 ,是否存在常数k,使得点B在轨迹C上,若存在,求k的值;若不存在,说明理由.
,是否存在常数k,使得点B在轨迹C上,若存在,求k的值;若不存在,说明理由.
 的方程为
的方程为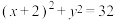 ,点
,点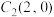 ,点M为圆
,点M为圆 上的任意一点,线段
上的任意一点,线段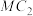 的垂直平分线与线段
的垂直平分线与线段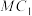 相交于点N.
相交于点N.(1)求点N的轨迹C的方程.
(2)已知点
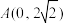 ,过点A且斜率为k的直线
,过点A且斜率为k的直线 交轨迹C于
交轨迹C于 两点,以
两点,以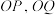 为邻边作平行四边形
为邻边作平行四边形 ,是否存在常数k,使得点B在轨迹C上,若存在,求k的值;若不存在,说明理由.
,是否存在常数k,使得点B在轨迹C上,若存在,求k的值;若不存在,说明理由.
您最近一年使用:0次
2019-04-02更新
|
486次组卷
|
3卷引用:【市级联考】江西省上饶市2019届高三第二次模拟考试数学(理)试题
名校
解题方法
5 . 椭圆 :
: 内有一点
内有一点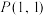
(1)求经过 并且以
并且以 为中点的弦所在直线方程;
为中点的弦所在直线方程;
(2)如果直线 :
: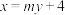 与椭圆
与椭圆 相交于
相交于 、
、 两点,求
两点,求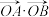 的取值范围.
的取值范围.
 :
: 内有一点
内有一点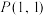
(1)求经过
 并且以
并且以 为中点的弦所在直线方程;
为中点的弦所在直线方程;(2)如果直线
 :
: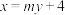 与椭圆
与椭圆 相交于
相交于 、
、 两点,求
两点,求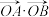 的取值范围.
的取值范围.
您最近一年使用:0次
2016-12-04更新
|
294次组卷
|
4卷引用:2015-2016学年四川省攀枝花十五中高二上学期期中理科数学试卷
名校
6 . 如图,曲线 由上半椭圆
由上半椭圆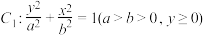 和部分抛物线
和部分抛物线
 连接而成,
连接而成, 的公共点为
的公共点为 ,其中
,其中 的离心率为
的离心率为 .
.
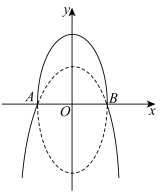
(Ⅰ)求 的值;
的值;
(Ⅱ)过点 的直线
的直线 与
与 分别交于
分别交于 (均异于点
(均异于点 ),若
),若 ,求直线
,求直线 的方程.
的方程.
 由上半椭圆
由上半椭圆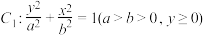 和部分抛物线
和部分抛物线
 连接而成,
连接而成, 的公共点为
的公共点为 ,其中
,其中 的离心率为
的离心率为 .
.
(Ⅰ)求
 的值;
的值;(Ⅱ)过点
 的直线
的直线 与
与 分别交于
分别交于 (均异于点
(均异于点 ),若
),若 ,求直线
,求直线 的方程.
的方程.
您最近一年使用:0次
2016-12-03更新
|
2454次组卷
|
12卷引用:四川省攀枝花市第十五中学2019-2020学年高二上学期第一次月考数学理科试卷
四川省攀枝花市第十五中学2019-2020学年高二上学期第一次月考数学理科试卷2016届广东省惠州市高三第一次调研考试数学理试卷12016届广东省惠州市高三第一次调研考试数学理试卷2河南省息县第一高级中学2017届高三下学期第三次适应性测试数学(理)试题贵州省思南中学2016-2017学年高二下学期期末考试数学(理)试题安徽省合肥庐阳高级中学2017-2018学年高二(上)期末考试理科数学试题福建省厦门一中2019-2020学年高二上学期10月月考数学试题(已下线)专题28 抛物线-十年(2011-2020)高考真题数学分项(已下线)考点30 直线与圆锥曲线-2021年新高考数学一轮复习考点扫描高中数学解题兵法 第八十八讲 重在构造、移花接木2023版 北师大版(2019) 选修第一册 名师精选卷 第九单元 直线与圆锥曲线的位置关系(已下线)专题24 解析几何解答题(理科)-3



