1 . 甲、乙两位同学组成学习小组进行项目式互助学习,在共同完成某个内容的互助学习后,甲、乙都参加了若干次测试,现从甲的测试成绩里随机抽取了7次成绩,从乙的测试成绩里随机抽取了9次成绩,数据如下:
甲:93 95 81 72 80 82 92
乙:85 82 77 80 94 86 92 84 85
经计算得出甲、乙两人的测试成绩的平均数均为85.
(1)求甲乙两位同学测试成绩的方差;
(2)为检验两组数据的差异性是否显著,可以计算统计量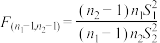 ,其中
,其中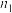 个数据的方差为
个数据的方差为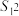 ,
,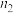 个数据的方差为
个数据的方差为 ,且
,且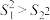 .若
.若 ,则认为两组数据有显著性差异,否则不能认为两组数据有显著性差异.若
,则认为两组数据有显著性差异,否则不能认为两组数据有显著性差异.若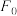 的临界值采用下表中的数据:
的临界值采用下表中的数据:
例如: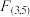 对应的临界值
对应的临界值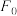 为5.41.请根据以上资料判断甲、乙两位同学进行项目式互助学习的效果是否有显著性差异.
为5.41.请根据以上资料判断甲、乙两位同学进行项目式互助学习的效果是否有显著性差异.
甲:93 95 81 72 80 82 92
乙:85 82 77 80 94 86 92 84 85
经计算得出甲、乙两人的测试成绩的平均数均为85.
(1)求甲乙两位同学测试成绩的方差;
(2)为检验两组数据的差异性是否显著,可以计算统计量
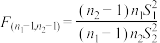 ,其中
,其中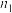 个数据的方差为
个数据的方差为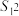 ,
,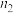 个数据的方差为
个数据的方差为 ,且
,且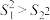 .若
.若 ,则认为两组数据有显著性差异,否则不能认为两组数据有显著性差异.若
,则认为两组数据有显著性差异,否则不能认为两组数据有显著性差异.若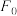 的临界值采用下表中的数据:
的临界值采用下表中的数据:
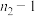 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 |
2 | 18.5 | 19.0 | 19.2 | 19.2 | 19.3 | 19.3 | 19.4 | 19.4 |
3 | 10.1 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8.85 |
4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 |
5 | 6.61 | 5.79 | 5.41 | 6.19 | 5.05 | 4.95 | 4.88 | 4.82 |
6 | 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 |
7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 |
8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 |
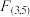 对应的临界值
对应的临界值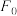 为5.41.请根据以上资料判断甲、乙两位同学进行项目式互助学习的效果是否有显著性差异.
为5.41.请根据以上资料判断甲、乙两位同学进行项目式互助学习的效果是否有显著性差异.
您最近一年使用:0次
名校
2 . 2020年1月,教育部《关于在部分高校开展基础学科招生改革试点工作的意见》印发,自2020年起,在部分高校开展基础学科招生改革试点(也称“强基计划”).强基计划聚焦高端芯片与软件、智能科技、新材料、先进制造和国家安全等关键领域以及国家人才紧缺的人文社会科学领域,选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生.新材料产业是重要的战略性新兴产业,下图是我国2011-2019年中国新材料产业市场规模及增长趋势图.其中柱状图表示新材料产业市场规模(单位:万亿元),折线图表示新材料产业市场规模年增长率( ).
).

(1)求2015年至2019年这5年的新材料产业市场规模的平均数;
(2)从2012年至2019年中随机挑选一年,求该年新材料产业市场规模较上一年的年增加量不少于6000亿元的概率;
(3)由图判断,从哪年开始连续三年的新材料产业市场规模年增长率的方差最大.(结论不要求证明)
 ).
).
(1)求2015年至2019年这5年的新材料产业市场规模的平均数;
(2)从2012年至2019年中随机挑选一年,求该年新材料产业市场规模较上一年的年增加量不少于6000亿元的概率;
(3)由图判断,从哪年开始连续三年的新材料产业市场规模年增长率的方差最大.(结论不要求证明)
您最近一年使用:0次
2020-05-18更新
|
448次组卷
|
4卷引用:2020届云南省昆明市高三“三诊一模”教学质量检测数学(文)试题
3 . 2020年1月,教育部《关于在部分高校开展基础学科招生改革试点工作的意见》印发,自2020年起,在部分高校开展基础学科招生改革试点(也称“强基计划”).强基计划聚焦高端芯片与软件、智能科技、新材料、先进制造和国家安全等关键领域以及国家人才紧缺的人文社会科学领域,选拔培养有志于服务国家重大战略需求且综合素质优秀或基础学科拔尖的学生.新材料产业是重要的战略性新兴产业,下图是我国2011-2019年中国新材料产业市场规模及增长趋势图.其中柱状图表示新材料产业市场规模(单位:万亿元),折线图表示新材料产业市场规模年增长率( ).
).
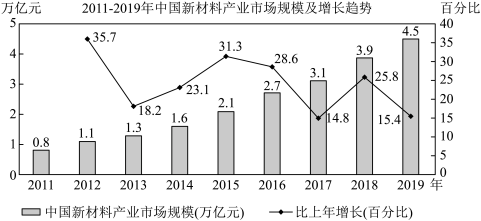
(1)求从2012年至2019年,每年新材料产业市场规模年增长量的平均数(精确到0.1);
(2)从2015年至2019年中随机挑选两年,求两年中至少有一年新材料产业市场规模年增长率超过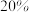 的概率;
的概率;
(3)由图判断,从哪年开始连续三年的新材料产业市场规模的方差最大. (结论不要求证明)
 ).
).
(1)求从2012年至2019年,每年新材料产业市场规模年增长量的平均数(精确到0.1);
(2)从2015年至2019年中随机挑选两年,求两年中至少有一年新材料产业市场规模年增长率超过
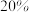 的概率;
的概率;(3)由图判断,从哪年开始连续三年的新材料产业市场规模的方差最大. (结论不要求证明)
您最近一年使用:0次
名校
4 . “中国大能手”是央视推出的一档大型职业技能挑战赛类节目,旨在通过该节目,在全社会传播和弘扬“劳动光荣、技能宝贵、创造伟大”的时代风尚.某公司准备派出选手代表公司参加“中国大能手”职业技能挑战赛.经过层层选拔,最后集中在甲、乙两位选手在一项关键技能的区分上,选手完成该项挑战的时间越少越好.已知这两位选手在15次挑战训练中,完成该项关键技能挑战所用的时间 (单位:秒)及挑战失败(用“×”表示)的情况如下表1:
(单位:秒)及挑战失败(用“×”表示)的情况如下表1:
据上表中的数据,应用统计软件得下表2:
(1)根据上述回归方程,预测甲、乙分别在下一次完成该项关键技能挑战所用的时间;
(2)若该公司只有一个参赛名额,根据以上信息,判断哪位选手代表公司参加职业技能挑战赛更合适?请说明你的理由.
 (单位:秒)及挑战失败(用“×”表示)的情况如下表1:
(单位:秒)及挑战失败(用“×”表示)的情况如下表1:序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
 | × | 96 | 93 | × | 92 | × | 90 | 86 | × | × | 83 | 80 | 78 | 77 | 75 |
 | × | 95 | × | 93 | × | 92 | × | 88 | 83 | × | 82 | 80 | 80 | 74 | 73 |
| 均值(单位:秒)方差 | 方差 | 线性回归方程 | |
| 甲 | 85 | 50.2 | 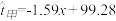 |
| 乙 | 84 | 54 |  |
(2)若该公司只有一个参赛名额,根据以上信息,判断哪位选手代表公司参加职业技能挑战赛更合适?请说明你的理由.
您最近一年使用:0次
2019-01-14更新
|
738次组卷
|
3卷引用:【市级联考】云南省昆明市2019届高三1月复习诊断测试理科数学试题
【市级联考】云南省昆明市2019届高三1月复习诊断测试理科数学试题(已下线)专题10.2 变量相关性与统计案例(精练)-2021年高考数学(理)一轮复习学与练重庆市第八中学2021-2022学年高二艺术班上学期期中数学试题
5 . “中国大能手”是央视推出的一档大型职业技能挑战赛类节目,旨在通过该节目,在全社会传播和弘扬“劳动光荣、技能宝贵、创造伟大”的时代风尚.某公司准备派出选手代表公司参加“中国大能手”职业技能挑战赛.经过层层选拔,最后集中在甲、乙两位选手在一项关键技能的区分上,选手完成该项挑战的时间越少越好.已知这两位选手在15次挑战训练中,完成该项关键技能挑战所用的时间(单位:秒)及挑战失败(用“×”表示)的情况如下表1:
据表1中甲、乙两选手完成该项关键技能挑战成功所用时间的数据,应用统计软件得下表2:
(1)在表1中,从选手甲完成挑战用时低于90秒的成绩中,任取2个,求这2个成绩都低于80秒的概率;
(2)若该公司只有一个参赛名额,以该关键技能挑战成绩为标准,根据以上信息,判断哪位选手代表公司参加职业技能挑战赛更合适?请说明你的理由.
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 甲 | × | 96 | 93 | × | 92 | × | 90 | 86 | × | × | 83 | 80 | 78 | 77 | 75 |
| 乙 | × | 95 | × | 93 | × | 92 | × | 88 | 83 | × | 82 | 80 | 80 | 74 | 73 |
| 数字特征 | 均值(单位:秒)方差 | 方差 |
| 甲 | 85 | 50.2 |
| 乙 | 84 | 54 |
(2)若该公司只有一个参赛名额,以该关键技能挑战成绩为标准,根据以上信息,判断哪位选手代表公司参加职业技能挑战赛更合适?请说明你的理由.
您最近一年使用:0次
11-12高一·全国·课后作业
6 . 假定下述数据是甲、乙两个供货商的交货天数:
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
甲:10 9 10 10 11 11 9 11 10 10
乙:8 10 14 7 10 11 10 8 15 12
估计两个供货商的交货情况,并问哪个供货商交货时间短一些,哪个供货商交货时间较具一致性与可靠性.
您最近一年使用:0次




