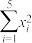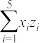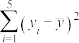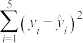1 . 2024年全国田径冠军赛暨全国田径大奖赛总决赛于6月30日在山东省日照市落幕.四川田径队的吴艳妮以12秒74分的成绩打破了100米女子跨栏的亚洲纪录,并夺得了2024年全国田径冠军赛女子100米跨栏决赛的冠军,通过跑道侧面的高清轨道摄像机记录了该运动员时间 (单位:
(单位: )与位移
)与位移 (单位:
(单位: )之间的关系,得到如下表数据:
)之间的关系,得到如下表数据:
画出散点图观察可得 与
与 之间近似为线性相关关系.
之间近似为线性相关关系.
(1)求出 关于
关于 的线性回归方程;
的线性回归方程;
(2)记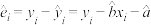 ,其中
,其中 为观测值,
为观测值,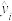 为预测值,
为预测值, 为对应
为对应 的残差,求前3项残差的和.
的残差,求前3项残差的和.
参考数据: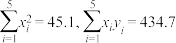 ,参考公式:
,参考公式: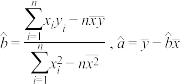 .
.
 (单位:
(单位: )与位移
)与位移 (单位:
(单位: )之间的关系,得到如下表数据:
)之间的关系,得到如下表数据: | 2.8 | 2.9 | 3 | 3.1 | 3.2 |
 | 24 | 25 | 29 | 32 | 34 |
 与
与 之间近似为线性相关关系.
之间近似为线性相关关系.(1)求出
 关于
关于 的线性回归方程;
的线性回归方程;(2)记
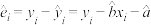 ,其中
,其中 为观测值,
为观测值,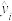 为预测值,
为预测值, 为对应
为对应 的残差,求前3项残差的和.
的残差,求前3项残差的和.参考数据:
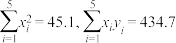 ,参考公式:
,参考公式: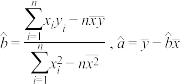 .
.
您最近一年使用:0次
解题方法
2 . 网络直播带货助力乡村振兴,它作为一种新颖的销售土特产的方式,受到社会各界的追捧.某直播间开展地标优品带货直播活动,其主播直播周期次数x(其中10场为一个周期)与产品销售额y(千元)的数据统计如下:
根据数据特点,甲认为样本点分布在指数型曲线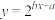 的周围,据此他对数据进行了一些初步处理.如下表:
的周围,据此他对数据进行了一些初步处理.如下表:
其中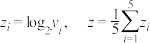
(1)请根据表中数据,建立y关于x的回归方程;
(2)乙认为样本点分布在直线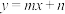 的周围,并计算得回归方程为
的周围,并计算得回归方程为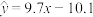 ,以及该回归模型的相关指数
,以及该回归模型的相关指数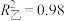 ,试比较甲、乙两人所建立的模型,谁的拟合效果更好?(
,试比较甲、乙两人所建立的模型,谁的拟合效果更好?( 精确到0.01)
精确到0.01)
附:对于一组数据 ,其回归直线
,其回归直线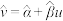 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为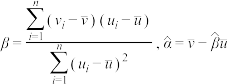 ,相关指数:
,相关指数: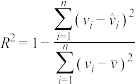 .
.
直播周期数x | 1 | 2 | 3 | 4 | 5 |
产品销售额y(千元) | 3 | 7 | 15 | 30 | 40 |
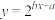 的周围,据此他对数据进行了一些初步处理.如下表:
的周围,据此他对数据进行了一些初步处理.如下表:
|
|
|
|
|
|
3.7 | 55 | 382 | 65 | 978 | 101 |
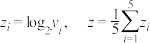
(1)请根据表中数据,建立y关于x的回归方程;
(2)乙认为样本点分布在直线
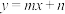 的周围,并计算得回归方程为
的周围,并计算得回归方程为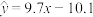 ,以及该回归模型的相关指数
,以及该回归模型的相关指数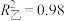 ,试比较甲、乙两人所建立的模型,谁的拟合效果更好?(
,试比较甲、乙两人所建立的模型,谁的拟合效果更好?( 精确到0.01)
精确到0.01)附:对于一组数据
 ,其回归直线
,其回归直线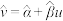 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为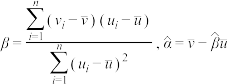 ,相关指数:
,相关指数: .
.
您最近一年使用:0次
解题方法
3 . 由于人们健康意识的提升,运动爱好者人群不断扩大,运动相关行业得到快速发展.某运动品牌专卖店从2019年至2023年的年销售额如下表:
(1)请根据表中的数据用最小二乘法求 与
与 的经验回归方程
的经验回归方程 ,并预测2024年该店的年销售额.
,并预测2024年该店的年销售额.
(2)该专卖店为了回馈广大消费者,推出了消费抽奖返现活动,规则如下:凡一次性消费满500元可抽奖1次,满1000元可抽奖2次.其中一次抽奖返现金额及概率如下表:
已知一位消费者一次性消费满500元的概率为 ,满1000元的概率为
,满1000元的概率为 ,求这位消费者抽奖返现金额
,求这位消费者抽奖返现金额 的分布列与期望.
的分布列与期望.
附:经验回归方程 中,
中,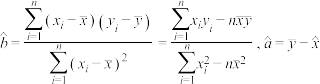 .
.
| 年份 | 2019 | 2020 | 2021 | 2022 | 2023 |
年份编号 | 1 | 2 | 3 | 4 | 5 |
年销售额 /万元 /万元 | 30 | 35 | 45 | 60 | 80 |
 与
与 的经验回归方程
的经验回归方程 ,并预测2024年该店的年销售额.
,并预测2024年该店的年销售额.(2)该专卖店为了回馈广大消费者,推出了消费抽奖返现活动,规则如下:凡一次性消费满500元可抽奖1次,满1000元可抽奖2次.其中一次抽奖返现金额及概率如下表:
| 返现金额 | 50 | 100 |
| 概率 |  |  |
 ,满1000元的概率为
,满1000元的概率为 ,求这位消费者抽奖返现金额
,求这位消费者抽奖返现金额 的分布列与期望.
的分布列与期望.附:经验回归方程
 中,
中,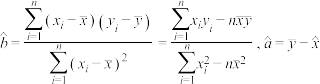 .
.
您最近一年使用:0次
解题方法
4 . 为深入学习贯彻习近平新时代中国特色社会主义思想,传播节能降碳和绿色发展理念,倡导绿色低碳生活方式,某市积极响应“节能减排,低碳生活”的号召,开展系列的措施控制碳排放.下表为该市统计的近5年内燃油车的新增数量,其中 为年份代号,
为年份代号, (单位:万辆)代表新增燃油车数量.
(单位:万辆)代表新增燃油车数量.
(1)计算相关系数 ,判断是否可以用线性回归模型拟合
,判断是否可以用线性回归模型拟合 与
与 的关系,当
的关系,当 时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.(保留到小数点后两位)
时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.(保留到小数点后两位)
(2)求 关于
关于 的线性回归方程,并据此估计该市2024年的新增燃油车数量.
的线性回归方程,并据此估计该市2024年的新增燃油车数量.
参考数据: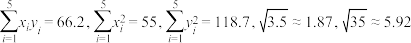
参考公式: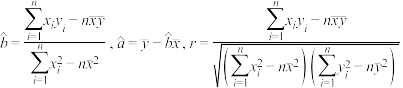
 为年份代号,
为年份代号, (单位:万辆)代表新增燃油车数量.
(单位:万辆)代表新增燃油车数量.年份 | 2019 | 2020 | 2021 | 2022 | 2023 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
新增燃油车 | 6.1 | 5.2 | 4.9 | 4 | 3.8 |
 ,判断是否可以用线性回归模型拟合
,判断是否可以用线性回归模型拟合 与
与 的关系,当
的关系,当 时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.(保留到小数点后两位)
时,可以认为两个变量有很强的线性相关性;否则,没有很强的线性相关性.(保留到小数点后两位)(2)求
 关于
关于 的线性回归方程,并据此估计该市2024年的新增燃油车数量.
的线性回归方程,并据此估计该市2024年的新增燃油车数量.参考数据:
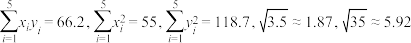
参考公式:
您最近一年使用:0次
名校
解题方法
5 . 商家项目投资的利润产生是一个复杂的系统结果.它与项目落地国的商业环境,政府执政能力,法律生态等都有重大的关联.如表所示是某项目在中国和南亚某国投资额和相应利润的统计表.
请选择平均利润较高的落地国,用最小二乘法求出回归直线方程为______ .
参考数据和公式: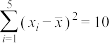 ,中国
,中国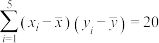 ,南亚某国
,南亚某国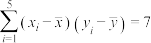 ,
,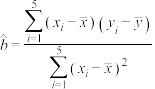 ,
, .
.
项目落地国 | 中国 | 南亚某国 | ||||||||
投资额 | 10 | 11 | 12 | 13 | 14 | 10 | 11 | 12 | 13 | 14 |
利润 | 11 | 12 | 14 | 16 | 19 | 12 | 13 | 13 | 14 | 15 |
参考数据和公式:
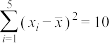 ,中国
,中国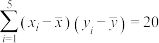 ,南亚某国
,南亚某国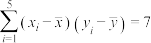 ,
,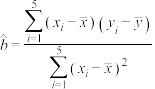 ,
, .
.
您最近一年使用:0次
解题方法
6 . 某品牌电脑专卖店的年销售量 与该年广告费用
与该年广告费用 有关,如表收集了4组观测数据:
有关,如表收集了4组观测数据:
以广告费用 为解释变量,销售量
为解释变量,销售量 为预报变量对这两个变量进行统计分析.
为预报变量对这两个变量进行统计分析.
(1)已知这两个变量呈线性相关关系,试建立 与
与 之间的回归方程
之间的回归方程 ;
;
(2)假如2017年该专卖店广告费用支出计划为10万元,根据你得到的模型,预测这一年的销售量 .
.
参考公式: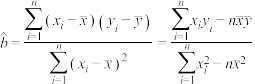 ,
,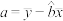 .
.
 与该年广告费用
与该年广告费用 有关,如表收集了4组观测数据:
有关,如表收集了4组观测数据:
| 1 | 4 | 5 | 6 |
| 30 | 40 | 60 | 50 |
 为解释变量,销售量
为解释变量,销售量 为预报变量对这两个变量进行统计分析.
为预报变量对这两个变量进行统计分析.(1)已知这两个变量呈线性相关关系,试建立
 与
与 之间的回归方程
之间的回归方程 ;
;(2)假如2017年该专卖店广告费用支出计划为10万元,根据你得到的模型,预测这一年的销售量
 .
.参考公式:
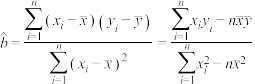 ,
,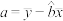 .
.
您最近一年使用:0次
名校
解题方法
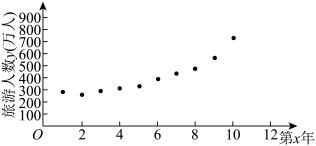
7 . 某景区的各景点从2009年取消门票实行免费开放后,旅游的人数不断地增加,不仅带动了该市淡季的旅游,而且优化了旅游产业的结构,促进了该市旅游向“观光、休闲、会展”三轮驱动的理想结构快速转变.下表是从2009年至2018年,该景点的旅游人数y(万人)与年份x的数据:
模型①:由最小二乘法公式求得y与x的线性回归方程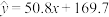 ;
;
模型②:由散点图的样本点分布,可以认为样本点集中在曲线 的附近.
的附近.
(1)根据表中数据,求模型②的回归方程 .(a精确到个位,b精确到0.001).
.(a精确到个位,b精确到0.001).
(2)根据下列表中的数据,比较两种模型的决定系数 ,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
参考公式、参考数据及说明:
①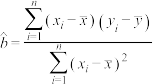 ,
,
②刻画回归效果的决定系数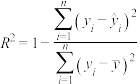 ;
;
③参考数据: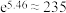 ,
,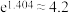
表中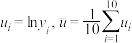 .
.
| 第x年 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 旅游人数y(万人) | 300 | 283 | 321 | 345 | 372 | 435 | 486 | 527 | 622 | 800 |
模型①:由最小二乘法公式求得y与x的线性回归方程
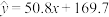 ;
;模型②:由散点图的样本点分布,可以认为样本点集中在曲线
 的附近.
的附近.(1)根据表中数据,求模型②的回归方程
 .(a精确到个位,b精确到0.001).
.(a精确到个位,b精确到0.001).(2)根据下列表中的数据,比较两种模型的决定系数
 ,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).
,并选择拟合精度更高、更可靠的模型,预测2021年该景区的旅游人数(单位:万人,精确到个位).| 回归方程 | ①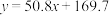 | ② |
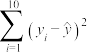 | 30407 | 14607 |
①
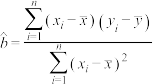 ,
,
②刻画回归效果的决定系数
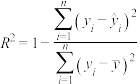 ;
;③参考数据:
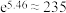 ,
,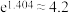
 | 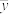 | 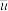 | 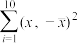 | 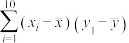 | 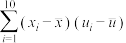 |
| 5.5 | 449 | 6.05 | 83 | 4195 | 9.00 |
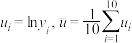 .
.
您最近一年使用:0次
名校
解题方法
8 . 高温可以使病毒中的蛋白质失去活性,从而达到杀死病毒的效果,某科研团队打算构建病毒的成活率与温度的某种数学模型,通过实验得到部分数据如下表:
由上表中的数据求得回归方程为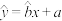 ,可以预测当温度为14℃时,病毒数量为( )
,可以预测当温度为14℃时,病毒数量为( )
参考公式: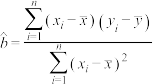 ,
,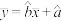
温度x(℃) | 6 | 8 | 10 |
病毒数量y(万个) | 30 | 22 | 20 |
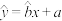 ,可以预测当温度为14℃时,病毒数量为( )
,可以预测当温度为14℃时,病毒数量为( )参考公式:
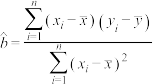 ,
,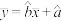
| A.12 | B.10 | C.9 | D.11 |
您最近一年使用:0次
2024-08-26更新
|
129次组卷
|
4卷引用:四川省仁寿第一中学校南校区2025届高三上学期10月月考数学试题
四川省仁寿第一中学校南校区2025届高三上学期10月月考数学试题四川省德阳市2023-2024学年高二下学期期末数学试题(已下线)专题2 回归方程 拟合效果(经典好题母题)【练】(已下线)第四章 统计 专题四 相关分析与回归分析 微点4 相关分析与回归分析综合训练【基础版】
名校
解题方法
9 . 某大学组织宣传小分队进行法律法规宣传,某宣传小分队记录了前9天每天普及的人数,得到下表:
(1)从这9天的数据中任选2天的数据,以X表示2天中普及人数不少于200人的天数,求X的分布列和数学期望;
(2)由于统计人员的疏忽,第5天的数据统计有误,如果去掉第5天的数据,试用剩下的数据求出每天普及的人数y关于天数x的线性回归方程.
参考数据: ,
, ,
, .附:对于一组数据(
.附:对于一组数据( ,
, ),(
),( ,
, ),……,(
),……,( ,
,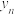 ),其回归直线
),其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: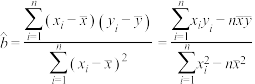 ,
, .
.
| 时间x(天) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 每天普及的人数y | 80 | 98 | 129 | 150 | 203 | 190 | 258 | 292 | 310 |
(2)由于统计人员的疏忽,第5天的数据统计有误,如果去掉第5天的数据,试用剩下的数据求出每天普及的人数y关于天数x的线性回归方程.
参考数据:
 ,
, ,
, .附:对于一组数据(
.附:对于一组数据( ,
, ),(
),( ,
, ),……,(
),……,( ,
,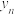 ),其回归直线
),其回归直线 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: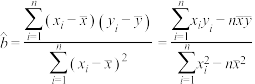 ,
, .
.
您最近一年使用:0次
2024-08-23更新
|
121次组卷
|
3卷引用:江苏省南通一中2023-2024学年高二年级数学下学期第二次月考(含答案)
江苏省南通一中2023-2024学年高二年级数学下学期第二次月考(含答案)黑龙江省哈尔滨市第四中学校2023-2024学年高二下学期期末考试数学试卷(已下线)专题2 回归方程 拟合效果(经典好题母题)【练】
解题方法
10 . 2024年2月10日至17日(正月初一至初八),“2024・内江市中区新春极光焰火草地狂欢节”在川南大草原举行,共举行了8场精彩的烟花秀节目.前5场的观众人数(单位:万人)与场次的统计数据如表所示:
(1)已知可用线性回归模型拟合y与x的关系,请建立y关于x的线性回归方程;
(2)若该烟花秀节目分A、B、C三个等次的票价,某机构随机调查了该烟花秀节目现场200位观众的性别与购票情况,得到的部分数据如表所示,请将 列联表补充完整,依据
列联表补充完整,依据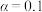 的独立性检验,能否认为该烟花秀节目的观众是否购买A等票与性别有关.
的独立性检验,能否认为该烟花秀节目的观众是否购买A等票与性别有关.
参考公式及参考数据:回归方程 中斜率与截距的最小二乘法估计公式分别为
中斜率与截距的最小二乘法估计公式分别为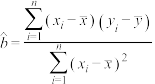 ,
, ,
, ,其中
,其中 .
.
场次编号x | 1 | 2 | 3 | 4 | 5 |
观众人数y | 0.7 | 0.8 | 1 | 1.2 | 1.3 |
(2)若该烟花秀节目分A、B、C三个等次的票价,某机构随机调查了该烟花秀节目现场200位观众的性别与购票情况,得到的部分数据如表所示,请将
 列联表补充完整,依据
列联表补充完整,依据 的独立性检验,能否认为该烟花秀节目的观众是否购买A等票与性别有关.
的独立性检验,能否认为该烟花秀节目的观众是否购买A等票与性别有关.购买A等票 | 购买非A等票 | 总计 | |
男性观众 | 50 | ||
女性观众 | 60 | ||
总计 | 100 | 200 |
 中斜率与截距的最小二乘法估计公式分别为
中斜率与截距的最小二乘法估计公式分别为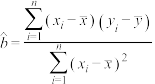 ,
, ,
, ,其中
,其中 .
.
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2024-08-21更新
|
97次组卷
|
2卷引用:广东省惠州市龙门县高级中学2023-2024学年高二下学期5月月考数学试题