名校
1 . 中华茶文化源远流长,博大精深,不但包含丰富的物质文化,还包含深厚的精神文化.其中绿茶在制茶过程中,在采摘后还需要经过杀青、揉捻、干燥这三道工序.现在某绿茶厂将采摘后的茶叶进行加工,其中杀青、揉捻、干燥这三道工序合格的概率分别为 ,每道工序的加工都相互独立,且茶叶加工中三道工序至少有一道工序合格的概率为
,每道工序的加工都相互独立,且茶叶加工中三道工序至少有一道工序合格的概率为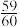 .三道工序加工都合格的绿茶为特级绿茶,恰有两道工序加工合格的绿茶为一级绿茶,恰有一道工序加工合格的绿茶为二级绿茶,其余的为不合格绿茶.
.三道工序加工都合格的绿茶为特级绿茶,恰有两道工序加工合格的绿茶为一级绿茶,恰有一道工序加工合格的绿茶为二级绿茶,其余的为不合格绿茶.
(1)在绿茶的三道工序中恰有两道工序加工合格的前提下,求杀青加工合格的概率;
(2)每盒绿茶(净重 )原材料及制作成本为30元,其中特级绿茶、一级绿茶、二级绿茶的出厂价分别为90元,60元,40元,而不合格绿茶则不进入市场.记经过三道工序制成的一盒绿茶的利润为
)原材料及制作成本为30元,其中特级绿茶、一级绿茶、二级绿茶的出厂价分别为90元,60元,40元,而不合格绿茶则不进入市场.记经过三道工序制成的一盒绿茶的利润为 元,求随机变量
元,求随机变量 的分布列及数学期望.
的分布列及数学期望.
 ,每道工序的加工都相互独立,且茶叶加工中三道工序至少有一道工序合格的概率为
,每道工序的加工都相互独立,且茶叶加工中三道工序至少有一道工序合格的概率为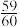 .三道工序加工都合格的绿茶为特级绿茶,恰有两道工序加工合格的绿茶为一级绿茶,恰有一道工序加工合格的绿茶为二级绿茶,其余的为不合格绿茶.
.三道工序加工都合格的绿茶为特级绿茶,恰有两道工序加工合格的绿茶为一级绿茶,恰有一道工序加工合格的绿茶为二级绿茶,其余的为不合格绿茶.(1)在绿茶的三道工序中恰有两道工序加工合格的前提下,求杀青加工合格的概率;
(2)每盒绿茶(净重
 )原材料及制作成本为30元,其中特级绿茶、一级绿茶、二级绿茶的出厂价分别为90元,60元,40元,而不合格绿茶则不进入市场.记经过三道工序制成的一盒绿茶的利润为
)原材料及制作成本为30元,其中特级绿茶、一级绿茶、二级绿茶的出厂价分别为90元,60元,40元,而不合格绿茶则不进入市场.记经过三道工序制成的一盒绿茶的利润为 元,求随机变量
元,求随机变量 的分布列及数学期望.
的分布列及数学期望.
您最近一年使用:0次
2024-04-19更新
|
633次组卷
|
2卷引用:黑龙江省双鸭山市友谊县高级中学2024届高三下学期高考模拟(一)数学试题
2 . 某机床厂生产一种精密零件,因生产流程比较复杂,所以成功率较低.从该厂某台机床生产的一批零件中,有放回的抽取3次,每次随机抽取1个,取出的3个零件中至多有2个是合格品的概率是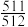 .假设这台机床生产的任意1个这种零件是合格品的概率相同,且每个零件生产之间互不影响.
.假设这台机床生产的任意1个这种零件是合格品的概率相同,且每个零件生产之间互不影响.
(1)求从该批零件中任取1个是合格品的概率;
(2)若这种零件合格品每个利润为10万元,不合格品的每个利润为 万元.现该机床生产4个这种零件,记这4个零件的利润为
万元.现该机床生产4个这种零件,记这4个零件的利润为 万元,求
万元,求 的分布列及数学期望
的分布列及数学期望 .
.
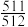 .假设这台机床生产的任意1个这种零件是合格品的概率相同,且每个零件生产之间互不影响.
.假设这台机床生产的任意1个这种零件是合格品的概率相同,且每个零件生产之间互不影响.(1)求从该批零件中任取1个是合格品的概率;
(2)若这种零件合格品每个利润为10万元,不合格品的每个利润为
 万元.现该机床生产4个这种零件,记这4个零件的利润为
万元.现该机床生产4个这种零件,记这4个零件的利润为 万元,求
万元,求 的分布列及数学期望
的分布列及数学期望 .
.
您最近一年使用:0次
名校
解题方法
3 . 一个小型制冰厂有3台同一型号的制冰设备,在一天内这3台设备只要有一台能正常工作,制冰厂就会有利润,当3台都无法正常工作时制冰厂就因停业而亏本(3台设备相互独立,3台都正常工作时利润最大).每台制冰设备的核心系统由3个同一型号的电子元件组成,3个元件能正常工作的概率都为 ,它们之间相互不影响,当系统中有不少于
,它们之间相互不影响,当系统中有不少于 的电子元件正常工作时,此台制冰设备才能正常工作.
的电子元件正常工作时,此台制冰设备才能正常工作.
(1)当 时,求一天内制冰厂不亏本的概率;
时,求一天内制冰厂不亏本的概率;
(2)若已知当前每台设备能正常工作的概率为0.6,根据以往经验可知,若制冰厂由于设备不能正常工作而停业一天,制冰厂将损失1万元,为减少经济损失,有以下两种方案可供选择参考:
方案1:更换3台设备的部分零件,使每台设备能正常工作的概率为0.85,更新费用共为600元.
方案2:对设备进行维护,使每台设备能正常工作的概率为0.75,设备维护总费用为 元.请从期望损失最小的角度判断如何决策?
元.请从期望损失最小的角度判断如何决策?
 ,它们之间相互不影响,当系统中有不少于
,它们之间相互不影响,当系统中有不少于 的电子元件正常工作时,此台制冰设备才能正常工作.
的电子元件正常工作时,此台制冰设备才能正常工作.(1)当
 时,求一天内制冰厂不亏本的概率;
时,求一天内制冰厂不亏本的概率;(2)若已知当前每台设备能正常工作的概率为0.6,根据以往经验可知,若制冰厂由于设备不能正常工作而停业一天,制冰厂将损失1万元,为减少经济损失,有以下两种方案可供选择参考:
方案1:更换3台设备的部分零件,使每台设备能正常工作的概率为0.85,更新费用共为600元.
方案2:对设备进行维护,使每台设备能正常工作的概率为0.75,设备维护总费用为
 元.请从期望损失最小的角度判断如何决策?
元.请从期望损失最小的角度判断如何决策?
您最近一年使用:0次
2023-06-30更新
|
360次组卷
|
7卷引用:湖南省名校联考联合体2022-2023学年高二下学期6月期末数学试题
湖南省名校联考联合体2022-2023学年高二下学期6月期末数学试题江西省龙南中学2022-2023学年高二下学期6月期末考试数学试题(已下线)考点18 决策的选择问题 2024届高考数学考点总动员(已下线)专题03 随机变量及其分布列-3(已下线)重组6 高二期末真题重组卷(湖南卷)A基础卷(已下线)第11题 利用均值解决决策型问题(压轴题)(已下线)第07讲 离散型随机变量及其分布列、数字特征(六大题型)(讲义)-2



