1 . “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽在《周髀算经》中注释了其理论证明,其基本思想是图形经过割补后面积不变.即通过如图所示的“弦图”,将勾股定理表述为:“勾股各自乘,并之,为弦实,开方除之,即弦”(其中 分别为勾股弦);证明方法叙述为:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实”,即
分别为勾股弦);证明方法叙述为:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实”,即 ,化简得
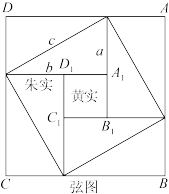
,化简得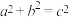 .现已知
.现已知 ,
, ,向外围大正方形
,向外围大正方形 区域内随机地投掷一枚飞镖,飞镖落在中间小正方形
区域内随机地投掷一枚飞镖,飞镖落在中间小正方形 内的概率是
内的概率是
 分别为勾股弦);证明方法叙述为:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实”,即
分别为勾股弦);证明方法叙述为:“按弦图,又可以勾股相乘为朱实二,倍之为朱实四,以勾股之差自相乘为中黄实,加差实,亦成弦实”,即 ,化简得
,化简得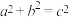 .现已知
.现已知 ,
, ,向外围大正方形
,向外围大正方形 区域内随机地投掷一枚飞镖,飞镖落在中间小正方形
区域内随机地投掷一枚飞镖,飞镖落在中间小正方形 内的概率是
内的概率是
A. | B. | C.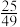 | D.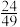 |
您最近一年使用:0次
2019-01-31更新
|
214次组卷
|
2卷引用:【市级联考】湖北省仙桃、天门、潜江市2019届高三上学期期末考试数学(文)试题
2 . 如图,点 的坐标为
的坐标为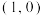 ,点
,点 的坐标为
的坐标为 ,函数
,函数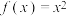 ,若在矩形
,若在矩形 内随机取一点,则此点取自阴影部分的概率等于
内随机取一点,则此点取自阴影部分的概率等于___________ .
 的坐标为
的坐标为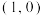 ,点
,点 的坐标为
的坐标为 ,函数
,函数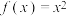 ,若在矩形
,若在矩形 内随机取一点,则此点取自阴影部分的概率等于
内随机取一点,则此点取自阴影部分的概率等于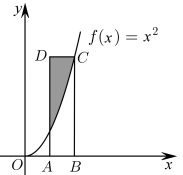
您最近一年使用:0次
2016-12-03更新
|
1595次组卷
|
17卷引用:湖北省天门、仙桃、潜江三市2016-2017学年高二下学期期末考试数学(理)试题
湖北省天门、仙桃、潜江三市2016-2017学年高二下学期期末考试数学(理)试题2015年全国普通高等学校招生统一考试理科数学(福建卷)2016届陕西西北工大附中高三下第六次训练理数学卷2017届湖南师大附中高三上月考三数学(理)试卷2017届湖南师大附中高三理上学期月考三数学试卷河北省大名县第一中学2018届高三上学期第二次月考(理)数学试题【全国市级联考】山西省康杰中学2017-2018学年高二下学期5月月考数学(理)试题(已下线)《高频考点解密》—解密06 定积分与微积分基本定理(已下线)专题11.6 几何概型(讲)【理】-《2020年高考一轮复习讲练测》(已下线)狂刷12 定积分与微积分基本定理-学易试题君之小题狂刷2020年高考数学(理)(已下线)专题10 定积分及其应用-十年(2011-2020)高考真题数学分项)(已下线)考点13 定积分与微积分基本定理-备战2021年高考数学(理)一轮复习考点一遍过(已下线)考点13 定积分与微积分基本定理-备战2022年高考数学(理)一轮复习考点帮陕西省渭南市瑞泉中学2021-2022学年高三上学期第一次质量检测数学试题甘肃省金昌市2021-2022学年高三上学期第一次联考数学(理)试题(已下线)考点48 几何概型-备战2022年高考数学典型试题解读与变式(已下线)专题19 概率统计多选、填空题(理科)-2



