解题方法
1 . 自1996年起,我国确定每年3月份最后一周的星期一为全国中小学生“安全教育日”.我国设立这一制度是为全面深入地推动中小学生安全教育工作,大力降低各类伤亡事故的发生率,切实做好中小学生的安全保护工作,促进他们健康成长.为了迎接“安全教育日”,某市将组织中学生进行一次安全知识有奖竞赛,竞赛奖励规则如下,得分在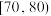 内的学生获三等奖,得分在
内的学生获三等奖,得分在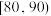 内的学生获二等奖,得分在
内的学生获二等奖,得分在 内的学生获一等奖,其他学生不获奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,统计如下:
内的学生获一等奖,其他学生不获奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,统计如下:
(1)若现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获一等奖的概率;
(2)若该市所有参赛学生的成绩X近似服从正态分布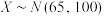 ,利用所得正态分布模型解决以下问题:
,利用所得正态分布模型解决以下问题:
(i)若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过85分的学生数(结果四舍五入到整数);
(ii)若从所有参赛学生中(参赛学生数大于100000)随机抽取4名学生进行访谈,设其中竞赛成绩在65分以上的学生数为Y,求随机变量Y的分布列及数学期望.
附参考数据:若随机变量X服从正态分布 ,则:
,则:
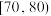 内的学生获三等奖,得分在
内的学生获三等奖,得分在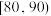 内的学生获二等奖,得分在
内的学生获二等奖,得分在 内的学生获一等奖,其他学生不获奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,统计如下:
内的学生获一等奖,其他学生不获奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,统计如下:| 成绩(分) | 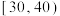 | 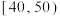 |  |  |  |  |  . . |
| 频数 | 6 | 12 | 18 | 24 | 18 | 12 | 10 |
(2)若该市所有参赛学生的成绩X近似服从正态分布
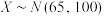 ,利用所得正态分布模型解决以下问题:
,利用所得正态分布模型解决以下问题:(i)若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过85分的学生数(结果四舍五入到整数);
(ii)若从所有参赛学生中(参赛学生数大于100000)随机抽取4名学生进行访谈,设其中竞赛成绩在65分以上的学生数为Y,求随机变量Y的分布列及数学期望.
附参考数据:若随机变量X服从正态分布
 ,则:
,则:
您最近一年使用:0次
2023-12-11更新
|
1497次组卷
|
4卷引用:专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)
(已下线)专题7.8 随机变量及其分布全章十一大压轴题型归纳(拔尖篇)-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)4.2.5 正态分布(第2课时) 正态分布(分层练习)-2023-2024学年高二数学同步精品课堂(人教B版2019选择性必修第二册)(已下线)题型27 5类概率统计大题综合解题技巧四川省宜宾市2024届高三上学期第一次诊断性测试理科数学试题
解题方法
2 . 积化和差的重要应用在于求解傅里叶级数.为了解学生掌握该组公式的情况,在高一、高三两个年级中随机抽取了100名学生进行考查,其中高三年级的学生占 ,其他相关数据如下表:
,其他相关数据如下表:
(1)请完成2×2列联表,依据小概率值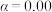 1的独立性检验,分析“对公式的掌握情况”与“学生所在年级”是否有关?
1的独立性检验,分析“对公式的掌握情况”与“学生所在年级”是否有关?
(2)以频率估计概率,从该校高一年级学生中抽取3名学生,记合格的人数为X,求X的分布列和数学期望.
附表及公式:
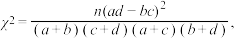 其中
其中
 ,其他相关数据如下表:
,其他相关数据如下表:| 合格 | 不合格 | 总计 | |
| 高三年级学生 | 54 | ||
| 高一年级学生 | 16 | ||
| 总计 | 100 |
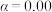 1的独立性检验,分析“对公式的掌握情况”与“学生所在年级”是否有关?
1的独立性检验,分析“对公式的掌握情况”与“学生所在年级”是否有关?(2)以频率估计概率,从该校高一年级学生中抽取3名学生,记合格的人数为X,求X的分布列和数学期望.
附表及公式:
 | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
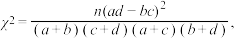 其中
其中
您最近一年使用:0次
名校
3 . 某企业因技术升级,决定从2023年起实现新的绩效方案.方案起草后,为了解员工对新绩效方案是否满意,决定采取如下“随机化回答技术”进行问卷调查:
一个袋子中装有三个大小相同的小球,其中1个黑球,2个白球.企业所有员工从袋子中有放回的随机摸两次球,每次摸出一球.约定“若两次摸到的球的颜色不同,则按方式一回答问卷,否则按方式二回答问卷”.
方式一:若第一次摸到的是白球,则在问卷中画“○”,否则画“×”;
方式二:若你对新绩效方案满意,则在问卷中画“○”,否则画“×”.
当所有员工完成问卷调查后,统计画○,画×的比例.用频率估计概率,由所学概率知识即可求得该企业员工对新绩效方案的满意度的估计值.其中满意度 .
.
(1)求每名员工两次摸到的球的颜色不同的概率
(2)若该企业某部门有9名员工,用 表示其中按方式一回答问卷的人数,求
表示其中按方式一回答问卷的人数,求 的数学期望;
的数学期望;
(3)若该企业的所有调查问卷中,画“○”与画“×”的比例为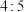 ,试估计该企业员工对新绩效方案的满意度.
,试估计该企业员工对新绩效方案的满意度.
一个袋子中装有三个大小相同的小球,其中1个黑球,2个白球.企业所有员工从袋子中有放回的随机摸两次球,每次摸出一球.约定“若两次摸到的球的颜色不同,则按方式一回答问卷,否则按方式二回答问卷”.
方式一:若第一次摸到的是白球,则在问卷中画“○”,否则画“×”;
方式二:若你对新绩效方案满意,则在问卷中画“○”,否则画“×”.
当所有员工完成问卷调查后,统计画○,画×的比例.用频率估计概率,由所学概率知识即可求得该企业员工对新绩效方案的满意度的估计值.其中满意度
 .
.(1)求每名员工两次摸到的球的颜色不同的概率
(2)若该企业某部门有9名员工,用
 表示其中按方式一回答问卷的人数,求
表示其中按方式一回答问卷的人数,求 的数学期望;
的数学期望;(3)若该企业的所有调查问卷中,画“○”与画“×”的比例为
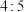 ,试估计该企业员工对新绩效方案的满意度.
,试估计该企业员工对新绩效方案的满意度.
您最近一年使用:0次
2023-06-01更新
|
592次组卷
|
12卷引用:上海市高桥中学2023-2024学年高二下学期期中考试数学试卷
上海市高桥中学2023-2024学年高二下学期期中考试数学试卷广东省江门市新会第一中学2023-2024学年高二下学期期中考试数学试题(已下线)7.4 二项分布与超几何分布(练习)浙江省杭州市长河高级中学2022-2023学年高二下学期期中数学试题江苏省南通市海门中学2022-2023学年高二下学期6月学情调研数学试题(已下线)黄金卷08(2024新题型)【巩固卷】章末检测试卷 (三) 单元测试A-湘教版(2019)选择性必修第二册(已下线)第一节 随机事件的概率与古典概型(北京专版)广东省深圳市2023届高三第一次调研数学试题(已下线)模块十 计数原理与统计概率-1专题24计数原理与概率与统计(解答题)北京市丰台区第二中学2023届高三三模数学试题
4 . 某市为了传承发展中华优秀传统文化,组织该市中学生进行了一次文化知识有奖竞赛,竞赛奖励规则如下:得分在 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在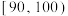 内的学生获得一等奖,其他学生不得奖,为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了样本频率分布直方图,如图所示.
内的学生获得一等奖,其他学生不得奖,为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了样本频率分布直方图,如图所示.
(2)若该市所有参赛学生的成绩X近似服从正态分布 ,其中
,其中 ,
, 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
为样本平均数的估计值,利用所得正态分布模型解决以下问题:
(i)若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
(ii)若从所有参赛学生中(参赛学生数大于10000)随机取3名学生进行访谈,设其中竞赛成绩在64分以上的学生数为 ,求随机变量
,求随机变量 的分布列和期望.
的分布列和期望.
附参考数据,若随机变量X服从正态分布 ,则
,则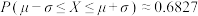 ,
,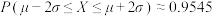 ,
,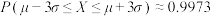 .
.
 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在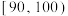 内的学生获得一等奖,其他学生不得奖,为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了样本频率分布直方图,如图所示.
内的学生获得一等奖,其他学生不得奖,为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,并以此为样本绘制了样本频率分布直方图,如图所示.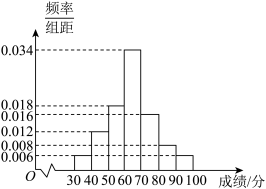
(2)若该市所有参赛学生的成绩X近似服从正态分布
 ,其中
,其中 ,
, 为样本平均数的估计值,利用所得正态分布模型解决以下问题:
为样本平均数的估计值,利用所得正态分布模型解决以下问题:(i)若该市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
(ii)若从所有参赛学生中(参赛学生数大于10000)随机取3名学生进行访谈,设其中竞赛成绩在64分以上的学生数为
 ,求随机变量
,求随机变量 的分布列和期望.
的分布列和期望.附参考数据,若随机变量X服从正态分布
 ,则
,则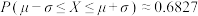 ,
,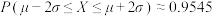 ,
,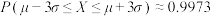 .
.
您最近一年使用:0次
2023-02-20更新
|
4141次组卷
|
11卷引用:第七章 随机变量及其分布 讲核心 02
(已下线)第七章 随机变量及其分布 讲核心 02辽宁省沈阳铁路实验中学2023-2024学年高二下学期4月阶段测试数学试卷广东省广州市天河区2021-2022学年高二下学期期末数学试题(已下线)第七章 随机变量及其分布 讲核心 02(已下线)7.5 正态分布 (精练)河北省石家庄市正中实验中学2022-2023学年高二下学期4月月考数学试题四川省内江市第六中学2022-2023学年高三上学期入学考试数学(理科)试题(已下线)专题50 正态分布-2山西省阳泉市2023届高三上学期期末数学试题湖南省长沙市雅礼中学2022-2023学年高三上学期月考(四)数学试题陕西省西安市西北工业大学附属中学2023届高三下学期第八次适应性训练理科数学试题
名校
解题方法
5 . 为了迎接4月23日“世界图书日”,我市将组织中学生进行一次文化知识有奖竞赛,竞赛奖励规则如下,得分在 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在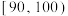 内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,统计如下
内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,统计如下
(1)若现从该样本中随机抽取两名学生的竞赛成绩,求这两名学生中恰有一名学生获奖的概率;
(2)若我市所有参赛学生的成绩 近似服从正态分布
近似服从正态分布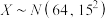 ,利用所得正态分布模型解决以下问题:
,利用所得正态分布模型解决以下问题:
(ⅰ)若我市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
(ⅱ)若从所有参赛学生中(参赛学生数大于100000)随机抽取3名学生进行访谈,设其中竞赛成绩在64分以上的学生数为 ,求随机变量
,求随机变量 的分布列及均值.
的分布列及均值.
附参考数据:若随机变量 服从正态分布
服从正态分布 ,则
,则
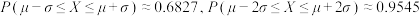 ,
,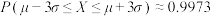 .
.
 内的学生获三等奖,得分在
内的学生获三等奖,得分在 内的学生获二等奖,得分在
内的学生获二等奖,得分在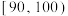 内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,统计如下
内的学生获一等奖,其他学生不得奖.为了解学生对相关知识的掌握情况,随机抽取100名学生的竞赛成绩,统计如下| 成绩(分) | 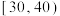 | 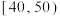 |  |  |  |  | 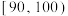 |
| 频数 | 6 | 12 | 18 | 34 | 16 | 8 | 6 |
(2)若我市所有参赛学生的成绩
 近似服从正态分布
近似服从正态分布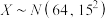 ,利用所得正态分布模型解决以下问题:
,利用所得正态分布模型解决以下问题:(ⅰ)若我市共有10000名学生参加了竞赛,试估计参赛学生中成绩超过79分的学生数(结果四舍五入到整数);
(ⅱ)若从所有参赛学生中(参赛学生数大于100000)随机抽取3名学生进行访谈,设其中竞赛成绩在64分以上的学生数为
 ,求随机变量
,求随机变量 的分布列及均值.
的分布列及均值.附参考数据:若随机变量
 服从正态分布
服从正态分布 ,则
,则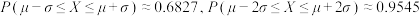 ,
,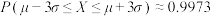 .
.
您最近一年使用:0次
2023-08-18更新
|
772次组卷
|
4卷引用:7.5 正态分布(6大题型)精练-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)
(已下线)7.5 正态分布(6大题型)精练-2023-2024学年高二数学题型分类归纳讲与练(人教A版2019选择性必修第三册)湖北省武汉市育才高级中学2023-2024学年高二下学期六月月考数学试卷河南省周口市项城市第三高级中学2022-2023学年高二下学期第三次考试数学试卷(A)江苏省南京市六校联合体2022-2023学年高二下学期5月调研数学试题
6 . 青少年近视问题备受社会各界广泛关注,某研究机构为了解学生对预防近视知识的掌握程度,对某校学生进行问卷调查,并随机抽取200份问卷,发现其得分(满分:100分)都在区间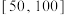 中,并将数据分组,制成如下频率分布表:
中,并将数据分组,制成如下频率分布表:
(1)试估计这200份问卷得分的平均值(同一组中的数据用该组区间的中点值代表);
(2)用样本估计总体,用频率估计概率,从该校学生中随机抽取4人深入调查,设X为抽取的4人中得分在 的人数,求
的人数,求 的分布列与数学期望.
的分布列与数学期望.
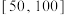 中,并将数据分组,制成如下频率分布表:
中,并将数据分组,制成如下频率分布表:| 分数 |  |  |  |  |  |
| 频率 | 0.15 | 0.25 |  | 0.30 | 0.10 |
(2)用样本估计总体,用频率估计概率,从该校学生中随机抽取4人深入调查,设X为抽取的4人中得分在
 的人数,求
的人数,求 的分布列与数学期望.
的分布列与数学期望.
您最近一年使用:0次
2023-01-31更新
|
567次组卷
|
6卷引用:7.4.1 二项分布——随堂检测
(已下线)7.4.1 二项分布——随堂检测(已下线)第七章 随机变量及其分布(A卷·知识通关练)(2)新高考地区2022-2023学年高三下学期开学考数学试卷江西省赣州市、河南省开封市(多地区学校)2023届下学期高三开学考试数学(理)试题河南省开封市五县2022-2023学年高三下学期开学考试理科数学试题(已下线)山东省济南市2022届高三二模数学试题变式题17-22



