1 . 我省某市为吸引游客,推出免费门票项目.该市设置自然风光类、历史文化类、特色体验类三个免费票抽奖机,自然风光类抽中的概率为 ,历史文化类、特色体验类抽中的概率均为
,历史文化类、特色体验类抽中的概率均为 ,这三类抽奖之间互不影响.规定凡在该市的景区游玩的游客,每位游客可在每个抽奖机中至多抽奖一次,每次抽奖至多抽中一个免费票景点.
,这三类抽奖之间互不影响.规定凡在该市的景区游玩的游客,每位游客可在每个抽奖机中至多抽奖一次,每次抽奖至多抽中一个免费票景点.
(1)若甲游客在三个抽奖机中各抽奖一次,设X表示甲获得免费票景点个数,求X的分布列和数学期望;
(2)乙游客从这三个抽奖机中随机选取两个抽奖,已知乙抽中(至少抽中一个),求乙在自然风光类、特色体验类抽奖机中抽中的概率.
 ,历史文化类、特色体验类抽中的概率均为
,历史文化类、特色体验类抽中的概率均为 ,这三类抽奖之间互不影响.规定凡在该市的景区游玩的游客,每位游客可在每个抽奖机中至多抽奖一次,每次抽奖至多抽中一个免费票景点.
,这三类抽奖之间互不影响.规定凡在该市的景区游玩的游客,每位游客可在每个抽奖机中至多抽奖一次,每次抽奖至多抽中一个免费票景点.(1)若甲游客在三个抽奖机中各抽奖一次,设X表示甲获得免费票景点个数,求X的分布列和数学期望;
(2)乙游客从这三个抽奖机中随机选取两个抽奖,已知乙抽中(至少抽中一个),求乙在自然风光类、特色体验类抽奖机中抽中的概率.
您最近一年使用:0次
名校
解题方法
2 . 箱中装有大小相同的黄、白两种颜色的乒乓球,黄、白乒乓球的数量比为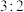 .现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过
.现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过 次,以
次,以 表示取球结束时已取到白球的次数.
表示取球结束时已取到白球的次数.
(1)求 的分布列;
的分布列;
(2)求 的数学期望.
的数学期望.
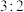 .现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过
.现从箱中每次任意取出一个球,若取出的是黄球则结束,若取出的是白球,则将其放回箱中,并继续从箱中任意取出一个球,但取球的次数最多不超过 次,以
次,以 表示取球结束时已取到白球的次数.
表示取球结束时已取到白球的次数.(1)求
 的分布列;
的分布列;(2)求
 的数学期望.
的数学期望.
您最近一年使用:0次
名校
3 . 某学校组织游戏活动,规则是学生从盒子中有放回的摸球且每次只能摸取1个球,每次摸球结果相互独立,盒中有1分和2分的球若干,摸到1分球的概率为 ,摸到2分球的概率为
,摸到2分球的概率为 .
.
(1)若学生甲摸球2次,其总得分记为 ,求随机变量
,求随机变量 的分布列与期望;
的分布列与期望;
(2)学生甲、乙各摸5次球,最终得分若相同,则都不获得奖励;若不同,则得分多者获得奖励.已知甲前3次摸球得了6分,求乙获得奖励的概率.
 ,摸到2分球的概率为
,摸到2分球的概率为 .
.(1)若学生甲摸球2次,其总得分记为
 ,求随机变量
,求随机变量 的分布列与期望;
的分布列与期望;(2)学生甲、乙各摸5次球,最终得分若相同,则都不获得奖励;若不同,则得分多者获得奖励.已知甲前3次摸球得了6分,求乙获得奖励的概率.
您最近一年使用:0次
2024-05-13更新
|
1750次组卷
|
6卷引用:广西南宁市第三中学2024届高三下学期校二模数学试题
名校
解题方法
4 . 某沙漠地区经过治理,生态系统得到很大改善,野生动物数量有所增加.为调查该地区植物覆盖面积与某种野生动物数量的关系,将其分成面积相近的若干个地块,从这些地块中随机抽取20个作为样区,调查得到样本数据 ,其中
,其中 ,和
,和 ,分别表示第
,分别表示第 个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量(单位:只),并计算得
个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量(单位:只),并计算得 .
.
(1)求样本 的相关系数(精确到0.01),并推断这种野生动物的数量y(单位:只)和植物覆盖面积x(单位:公顷)的相关程度;
的相关系数(精确到0.01),并推断这种野生动物的数量y(单位:只)和植物覆盖面积x(单位:公顷)的相关程度;
(2)已知20个样区中有8个样区的这种野生动物数量低于样本平均数,从20个样区中随机抽取2个,记抽到这种野生动物数量低于样本平均数的样区的个数为X,求随机变量X的分布列.
附:相关系数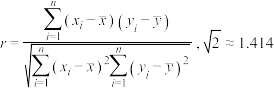
 ,其中
,其中 ,和
,和 ,分别表示第
,分别表示第 个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量(单位:只),并计算得
个样区的植物覆盖面积(单位:公顷)和这种野生动物的数量(单位:只),并计算得 .
.(1)求样本
 的相关系数(精确到0.01),并推断这种野生动物的数量y(单位:只)和植物覆盖面积x(单位:公顷)的相关程度;
的相关系数(精确到0.01),并推断这种野生动物的数量y(单位:只)和植物覆盖面积x(单位:公顷)的相关程度;(2)已知20个样区中有8个样区的这种野生动物数量低于样本平均数,从20个样区中随机抽取2个,记抽到这种野生动物数量低于样本平均数的样区的个数为X,求随机变量X的分布列.
附:相关系数
您最近一年使用:0次
2024-03-03更新
|
2135次组卷
|
13卷引用:广西南宁市第二中学2023-2024学年高三下学期5月月考数学试题
广西南宁市第二中学2023-2024学年高三下学期5月月考数学试题广东省广州市天河区2024届高三毕业班综合测试(二)数学试卷(已下线)热点8-2 概率与统计综合(10题型+满分技巧+限时检测)(已下线)专题08 统计案例分析(分层练)(三大题型+8道精选真题)(已下线)8.1 成对数据的统计相关性(分层练习,5大题型)-2023-2024学年高二数学同步精品课堂(人教A版2019选择性必修第三册)(已下线)第八章 成对数据的统计分析(知识归纳+题型突破)-2023-2024学年高二数学单元速记·巧练(沪教版2020选择性必修第二册)(已下线)第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)9.1 线性回归分析(2)(已下线)专题8.1 成对数据的统计相关性【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)(已下线)情境6 建设生态文明四川省南充高中2023-2024学年高三下学期第十三次月考理科数学试卷(附答案)(已下线)专题6 回归分析与独立性检验复杂问题【练】(高二期末压轴专项)(已下线)第四章 统计 专题二 统计相关性与回归分析 微点3 相关分析与回归分析(三)【培优版】
名校
5 . 某校为了丰富学生课余生活,体育节组织定点投篮比赛.为了解学生喜欢篮球是否与性别有关,随机抽取了男、女同学各100名进行调查,部分数据如表所示:
(1)根据所给数据完成上表,依据小概率值 的
的 独立性检验,能否据此推断该校学生喜欢篮球与性别有关?
独立性检验,能否据此推断该校学生喜欢篮球与性别有关?
(2)篮球指导老师从喜欢篮球的学生中抽取了2名男生和1名女生进行投篮示范.已知这两名男生投进的概率均为 ,这名女生投进的概率为
,这名女生投进的概率为 ,每人投篮一次,假设各人投篮相互独立,求3人投进总次数
,每人投篮一次,假设各人投篮相互独立,求3人投进总次数 的分布列和数学期望.
的分布列和数学期望.
附:
喜欢篮球 | 不喜欢篮球 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 |
 的
的 独立性检验,能否据此推断该校学生喜欢篮球与性别有关?
独立性检验,能否据此推断该校学生喜欢篮球与性别有关?(2)篮球指导老师从喜欢篮球的学生中抽取了2名男生和1名女生进行投篮示范.已知这两名男生投进的概率均为
 ,这名女生投进的概率为
,这名女生投进的概率为 ,每人投篮一次,假设各人投篮相互独立,求3人投进总次数
,每人投篮一次,假设各人投篮相互独立,求3人投进总次数 的分布列和数学期望.
的分布列和数学期望.附:

| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2024-02-24更新
|
2109次组卷
|
6卷引用:广西壮族自治区南宁市第三中学、柳州高级中学2024届高三下学期一轮复习诊断性联考数学试卷
广西壮族自治区南宁市第三中学、柳州高级中学2024届高三下学期一轮复习诊断性联考数学试卷(已下线)专题08 平面向量、概率、统计、计数原理(已下线)【一题多变】 分类变量 独立检验河北省保定市高碑店市崇德实验中学2024届高三下学期3月月考数学试题(已下线)专题8.4 统计分析大题专项训练【六大题型】-2023-2024学年高二数学举一反三系列(人教A版2019选择性必修第三册)2024届河南省驻马店市经开区高考三模数学试卷
名校
解题方法
6 . 随着寒冷冬季的到来,羽绒服进入了销售旺季,某调查机构随机调查了400人,询问他们选购羽绒服时更关注保暖性能还是更关注款式设计,得到以下的 列联表:
列联表:
(1)是否有 的把握认为男性和女性在选购羽线服时的关注点有差异?
的把握认为男性和女性在选购羽线服时的关注点有差异?
(2)若从这400人中按男女比例用分层抽样的方法抽取5人进行采访,再从这5人中任选2人赠送羽线服,记 为抽取的2人中女生的人数,求
为抽取的2人中女生的人数,求 的分布列和数学期望.
的分布列和数学期望.
附: .
.
 列联表:
列联表:更关注保暖性能 | 更关注款式设计 | 合计 | |
女性 | 160 | 80 | 240 |
男性 | 120 | 40 | 160 |
合计 | 280 | 120 | 400 |
 的把握认为男性和女性在选购羽线服时的关注点有差异?
的把握认为男性和女性在选购羽线服时的关注点有差异?(2)若从这400人中按男女比例用分层抽样的方法抽取5人进行采访,再从这5人中任选2人赠送羽线服,记
 为抽取的2人中女生的人数,求
为抽取的2人中女生的人数,求 的分布列和数学期望.
的分布列和数学期望.附:
 .
.
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2024-01-10更新
|
476次组卷
|
4卷引用:广西部分学校2024届高三下学期开学考试数学试题
名校
解题方法
7 . 某调查小组为了解本市不同年龄段的肺炎患者在肺炎确诊两周内的治疗情况,在肺炎患者中随机抽取100人进行调查,并将调查结果整理如下:
(1)试判断是否有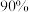 的把握认为该市肺炎患者在肺炎确诊两周内治愈与年龄有关;
的把握认为该市肺炎患者在肺炎确诊两周内治愈与年龄有关;
(2)现从样本中肺炎确诊两周内未治愈的人群中用分层抽样法抽取6人做进一步调查,然后从这6人中随机抽取3人填写调查问卷,记这3人中12岁以下的人数为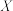 ,求
,求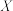 的分布列与数学期望.
的分布列与数学期望.
附:
 ,其中
,其中 .
.
| 两周内治愈 | 两周内未治愈 | |
| 12岁以上(含12岁) | 45 | 15 |
| 12岁以下 | 25 | 15 |
(1)试判断是否有
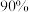 的把握认为该市肺炎患者在肺炎确诊两周内治愈与年龄有关;
的把握认为该市肺炎患者在肺炎确诊两周内治愈与年龄有关;(2)现从样本中肺炎确诊两周内未治愈的人群中用分层抽样法抽取6人做进一步调查,然后从这6人中随机抽取3人填写调查问卷,记这3人中12岁以下的人数为
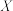 ,求
,求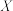 的分布列与数学期望.
的分布列与数学期望.附:
 | 0.150 | 0.100 | 0.050 | 0.025 |
 | 2.072 | 2.706 | 3.841 | 5.024 |
 ,其中
,其中 .
.
您最近一年使用:0次
名校
8 . 规定抽球试验规则如下:盒子中初始装有一个白球和两个红球,每次有放回的任取一个,连续取两次,将以上过程记为一轮.如果每一轮取到的两个球都是白球,则记该轮为成功,否则记为失败.在抽取过程中,如果某一轮成功,则停止:否则,在盒子中再放入一个红球,然后接着进行下一轮抽球,如此不断继续下去,直至成功.
(1)某人进行该抽球试验时,最多进行三轮,即使第三轮不成功,也停止抽球,记其进行抽球试验的轮次数为随机变量 ,求
,求 的分布列和数学期望;
的分布列和数学期望;
(2)为验证抽球试验成功的概率不超过 ,有1500名数学爱好者独立的进行该抽球试验,记
,有1500名数学爱好者独立的进行该抽球试验,记 表示成功时抽球试验的轮次数,
表示成功时抽球试验的轮次数, 表示对应的人数,部分统计数据如右表:
表示对应的人数,部分统计数据如右表:
求 关于
关于 的回归方程
的回归方程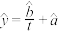 ,并预测成功的总人数(精确到1).
,并预测成功的总人数(精确到1).
附:经验回归方程系数: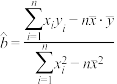 ,
, ;
;
参考数据: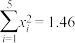 ,
,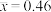 ,
,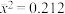 (其中
(其中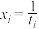 ,
,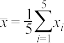 ).
).
(1)某人进行该抽球试验时,最多进行三轮,即使第三轮不成功,也停止抽球,记其进行抽球试验的轮次数为随机变量
 ,求
,求 的分布列和数学期望;
的分布列和数学期望;(2)为验证抽球试验成功的概率不超过
 ,有1500名数学爱好者独立的进行该抽球试验,记
,有1500名数学爱好者独立的进行该抽球试验,记 表示成功时抽球试验的轮次数,
表示成功时抽球试验的轮次数, 表示对应的人数,部分统计数据如右表:
表示对应的人数,部分统计数据如右表: | 1 | 2 | 3 | 4 | 5 |
 | 256 | 100 | 66 | 48 | 30 |
 关于
关于 的回归方程
的回归方程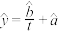 ,并预测成功的总人数(精确到1).
,并预测成功的总人数(精确到1).附:经验回归方程系数:
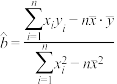 ,
, ;
;参考数据:
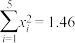 ,
,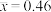 ,
,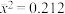 (其中
(其中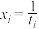 ,
,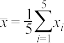 ).
).
您最近一年使用:0次
2023-12-20更新
|
452次组卷
|
2卷引用:广西壮族自治区广西贵港市、百色市、河池市2023-2024学年高三上学期11月质量调研联考数学试题
名校
9 . 某研究机构随机抽取了新近上映的某部影片的120名观众,对他们是否喜欢这部影片进行了调查,得到如下数据(单位:人):
根据上述信息,解决下列问题:
(1)根据小概率值 的独立性检验,分析观众喜欢该影片与观众的性别是否有关;
的独立性检验,分析观众喜欢该影片与观众的性别是否有关;
(2)从不喜欢该影片的观众中采用分层抽样的方法,随机抽取6人.现从6人中随机抽取2人,若所选2名观众中女性人数为X,求X的分布列及数学期望.
附: ,其中
,其中 .
.
喜欢 | 不喜欢 | 合计 | |
男性 | 40 | 30 | 70 |
女性 | 35 | 15 | 50 |
合计 | 75 | 45 | 120 |
(1)根据小概率值
 的独立性检验,分析观众喜欢该影片与观众的性别是否有关;
的独立性检验,分析观众喜欢该影片与观众的性别是否有关;(2)从不喜欢该影片的观众中采用分层抽样的方法,随机抽取6人.现从6人中随机抽取2人,若所选2名观众中女性人数为X,求X的分布列及数学期望.
附:
 ,其中
,其中 .
.
| 0.15 | 0.10 | 0.05 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
您最近一年使用:0次
2023-07-06更新
|
832次组卷
|
6卷引用:广西南宁市武鸣区武鸣高级中学2024届高三上学期开学调研测试数学试题
广西南宁市武鸣区武鸣高级中学2024届高三上学期开学调研测试数学试题广西壮族自治区贵港市平南县中学2025届高三上学期9月月考数学试题云南师范大学附属中学2024届高三高考适应性月考卷(一)数学试题云南省宣威市第三中学2024届高三上学期开学收心考试数学试题云南省临沧市民族中学2024届高三上学期开学考试数学试题(已下线)第05讲 第八章 成对数据的统计分析 章末重点题型大总结-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)
名校
10 . 为了促进消费,某商场针对会员客户推出会员积分兑换商品活动:每位会员客户可在价值80元,90元,100元的 ,
, ,
, 三种商品中选择一种使用积分进行兑换,每10积分可兑换1元.已知参加活动的甲、乙两位客户各有1000积分,且甲兑换
三种商品中选择一种使用积分进行兑换,每10积分可兑换1元.已知参加活动的甲、乙两位客户各有1000积分,且甲兑换 ,
, ,
, 三种商品的概率分别为
三种商品的概率分别为 ,
, ,
, ,乙兑换
,乙兑换 ,
, ,
, 三种商品的概率分别为
三种商品的概率分别为 ,
, ,
, ,且他们兑换何种商品相互独立.
,且他们兑换何种商品相互独立.
(1)求甲、乙两人兑换同一种商品的概率;
(2)记 为两人兑换商品后的积分总余额,求
为两人兑换商品后的积分总余额,求 的分布列与期望
的分布列与期望
 ,
, ,
, 三种商品中选择一种使用积分进行兑换,每10积分可兑换1元.已知参加活动的甲、乙两位客户各有1000积分,且甲兑换
三种商品中选择一种使用积分进行兑换,每10积分可兑换1元.已知参加活动的甲、乙两位客户各有1000积分,且甲兑换 ,
, ,
, 三种商品的概率分别为
三种商品的概率分别为 ,
, ,
, ,乙兑换
,乙兑换 ,
, ,
, 三种商品的概率分别为
三种商品的概率分别为 ,
, ,
, ,且他们兑换何种商品相互独立.
,且他们兑换何种商品相互独立.(1)求甲、乙两人兑换同一种商品的概率;
(2)记
 为两人兑换商品后的积分总余额,求
为两人兑换商品后的积分总余额,求 的分布列与期望
的分布列与期望
您最近一年使用:0次
2023-11-23更新
|
1892次组卷
|
10卷引用:广西普通高中2024届高三跨市联合适应性训练检测卷数学试题
广西普通高中2024届高三跨市联合适应性训练检测卷数学试题广西桂林、柳州、贺州、崇左四市2024届高三上学期跨市联合适应性检测数学试题四川省雅安市雅安市联考2023-2024学年高三上学期期中考试数学(理)试题四川省绵阳市绵阳实验高级中学2024届高三上学期11月月考数学(理)试题(已下线)第二篇 “搞定”解答题前3个 专题3 概率统计解答题【讲】高三逆袭之路突破90分(已下线)第二篇 “搞定”解答题前3个 专题3 概率统计解答题【练】 高三逆袭之路突破90分(已下线)专题12 概率(3大易错点分析+解题模板+举一反三+易错题通关)(已下线)6.3.1离散型随机变量的均值(分层练习)-2023-2024学年高二数学同步精品课堂(北师大版2019选择性必修第一册)(已下线)第04讲 7.3.1离散型随机变量的均值-【帮课堂】2023-2024学年高二数学同步学与练(人教A版2019选择性必修第三册)(已下线)7.3.1 离散型随机变量的均值——课后作业(提升版)





