名校
解题方法
1 . 某学校食堂每天都会提供A,B两种套餐供学生选择(学生只能选择其中的一种),经过统计分析发现:学生第一天选择A套餐的概率为 ,选择
,选择 套餐的概率为
套餐的概率为 .而前一天选择了
.而前一天选择了 套餐的学生第二天选择
套餐的学生第二天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率为
套餐的概率为 ;前一天选择
;前一天选择 套餐的学生第二天选择
套餐的学生第二天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率也是
套餐的概率也是 ,如此往复.记同学甲第
,如此往复.记同学甲第 天选择
天选择 套餐的概率为
套餐的概率为 .
.
(1)求同学甲第二天选择 套餐的概率;
套餐的概率;
(2)证明:数列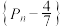 为等比数列;
为等比数列;
(3)从该校所有学生中随机抽取100名学生统计第二天选择 套餐的人数
套餐的人数 ,用
,用 表示这100名学生中恰有
表示这100名学生中恰有 名学生选择
名学生选择 套餐的概率,求
套餐的概率,求 取最大值时对应的
取最大值时对应的 的值.
的值.
 ,选择
,选择 套餐的概率为
套餐的概率为 .而前一天选择了
.而前一天选择了 套餐的学生第二天选择
套餐的学生第二天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率为
套餐的概率为 ;前一天选择
;前一天选择 套餐的学生第二天选择
套餐的学生第二天选择 套餐的概率为
套餐的概率为 ,选择
,选择 套餐的概率也是
套餐的概率也是 ,如此往复.记同学甲第
,如此往复.记同学甲第 天选择
天选择 套餐的概率为
套餐的概率为 .
.(1)求同学甲第二天选择
 套餐的概率;
套餐的概率;(2)证明:数列
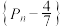 为等比数列;
为等比数列;(3)从该校所有学生中随机抽取100名学生统计第二天选择
 套餐的人数
套餐的人数 ,用
,用 表示这100名学生中恰有
表示这100名学生中恰有 名学生选择
名学生选择 套餐的概率,求
套餐的概率,求 取最大值时对应的
取最大值时对应的 的值.
的值.
您最近一年使用:0次
名校
2 . 甲乙两人参加知识竞赛活动,比赛规则如下:两人轮流随机抽题作答,答对积1分且对方不得分,答错不得分且对方积1分,然后换对方抽题作答,直到有领先2分者晋级,比赛结束.已知甲答对题目的概率为 ,乙答对题目的概率为P,答对与否相互独立,抽签决定首次答题方,已知两次答题后甲乙两人各积1分的概率为
,乙答对题目的概率为P,答对与否相互独立,抽签决定首次答题方,已知两次答题后甲乙两人各积1分的概率为 .记甲乙两人的答题总次数为
.记甲乙两人的答题总次数为 .
.
(1)求P;
(2)当 时,求甲得分X的分布列及数学期望;
时,求甲得分X的分布列及数学期望;
(3)若答题的总次数为n时,甲晋级的概率为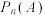 ,证明:
,证明: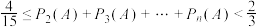 .
.
 ,乙答对题目的概率为P,答对与否相互独立,抽签决定首次答题方,已知两次答题后甲乙两人各积1分的概率为
,乙答对题目的概率为P,答对与否相互独立,抽签决定首次答题方,已知两次答题后甲乙两人各积1分的概率为 .记甲乙两人的答题总次数为
.记甲乙两人的答题总次数为 .
.(1)求P;
(2)当
 时,求甲得分X的分布列及数学期望;
时,求甲得分X的分布列及数学期望;(3)若答题的总次数为n时,甲晋级的概率为
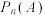 ,证明:
,证明: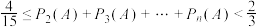 .
.
您最近一年使用:0次
23-24高二下·江苏·期末
3 . 《中华人民共和国国民经济和社会发展第十四个五年规划和2023年远景目标纲要》指出:要加强原创性、引领性科技攻关,坚决打赢关键核心技术攻坚战.某企业集中科研骨干力量,攻克系列关键技术,已成功实现离子注入机全谱系产品国产化,工艺段覆盖至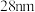 ,为我国芯片制造产业链补上重要一环.该企业使用新技术对某款芯片制造工艺进行改进.
,为我国芯片制造产业链补上重要一环.该企业使用新技术对某款芯片制造工艺进行改进.
(1)该款芯片生产有四道工序,前三道工序的生产互不影响,第四道是检测评估工序,包括智能自动检测与人工抽检.已知该款芯片在改进生产工艺前,前三道工序的次品率分别为 .
.
①求改进生产工艺前,该款芯片的次品率 ;
;
②在第四道工序中,部分芯片由智能检测系统进行筛选,其中部分次品芯片会被淘汰,筛选后的芯片及未经筛选的芯片进入流水线由工人进行抽样检验.记 表示事件“某芯片经过智能检测系统筛选”,
表示事件“某芯片经过智能检测系统筛选”, 表示事件“某芯片经人工抽检后合格”,求证:
表示事件“某芯片经人工抽检后合格”,求证: ;
;
(2)改进生产工艺后,该款芯片的某项质量指标 服从正态分布
服从正态分布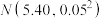 ,现从中随机抽取
,现从中随机抽取 个,这
个,这 个芯片中恰有
个芯片中恰有 个的质量指标
个的质量指标 位于区间
位于区间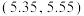 .
.
①若 ,以使得
,以使得 的最大
的最大 值作为
值作为 的估计值,求
的估计值,求 ;
;
②记这 个芯片的质量指标
个芯片的质量指标 的标准差为
的标准差为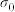 ,其中
,其中 个芯片的质量指标
个芯片的质量指标 的平均数为
的平均数为 ,标准差为
,标准差为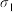 ,剩余芯片的质量指标
,剩余芯片的质量指标 的平均数为
的平均数为 ,标准差为
,标准差为 ,试写出
,试写出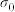 的计算式.
的计算式.
参考数据: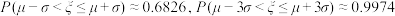 .
.
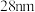 ,为我国芯片制造产业链补上重要一环.该企业使用新技术对某款芯片制造工艺进行改进.
,为我国芯片制造产业链补上重要一环.该企业使用新技术对某款芯片制造工艺进行改进.(1)该款芯片生产有四道工序,前三道工序的生产互不影响,第四道是检测评估工序,包括智能自动检测与人工抽检.已知该款芯片在改进生产工艺前,前三道工序的次品率分别为
 .
.①求改进生产工艺前,该款芯片的次品率
 ;
;②在第四道工序中,部分芯片由智能检测系统进行筛选,其中部分次品芯片会被淘汰,筛选后的芯片及未经筛选的芯片进入流水线由工人进行抽样检验.记
 表示事件“某芯片经过智能检测系统筛选”,
表示事件“某芯片经过智能检测系统筛选”, 表示事件“某芯片经人工抽检后合格”,求证:
表示事件“某芯片经人工抽检后合格”,求证: ;
;(2)改进生产工艺后,该款芯片的某项质量指标
 服从正态分布
服从正态分布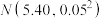 ,现从中随机抽取
,现从中随机抽取 个,这
个,这 个芯片中恰有
个芯片中恰有 个的质量指标
个的质量指标 位于区间
位于区间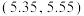 .
.①若
 ,以使得
,以使得 的最大
的最大 值作为
值作为 的估计值,求
的估计值,求 ;
;②记这
 个芯片的质量指标
个芯片的质量指标 的标准差为
的标准差为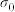 ,其中
,其中 个芯片的质量指标
个芯片的质量指标 的平均数为
的平均数为 ,标准差为
,标准差为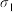 ,剩余芯片的质量指标
,剩余芯片的质量指标 的平均数为
的平均数为 ,标准差为
,标准差为 ,试写出
,试写出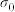 的计算式.
的计算式.参考数据:
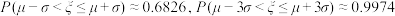 .
.
您最近一年使用:0次
名校
解题方法
4 . 一个袋子中有10个大小相同的球,其中红球7个,黑球3个.每次从袋中随机摸出1个球,摸出的球不再放回.
(1)求第2次摸到红球的概率;
(2)设第 次都摸到红球的概率为
次都摸到红球的概率为 ;第1次摸到红球的概率为
;第1次摸到红球的概率为 ;在第1次摸到红球的条件下,第2次摸到红球的概率为
;在第1次摸到红球的条件下,第2次摸到红球的概率为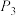 ;在第1,2次都摸到红球的条件下,第3次摸到红球的概率为
;在第1,2次都摸到红球的条件下,第3次摸到红球的概率为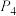 .求
.求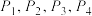 ;
;
(3)对于事件 ,当
,当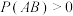 时,写出
时,写出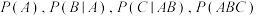 的等量关系式,并加以证明.
的等量关系式,并加以证明.
(1)求第2次摸到红球的概率;
(2)设第
 次都摸到红球的概率为
次都摸到红球的概率为 ;第1次摸到红球的概率为
;第1次摸到红球的概率为 ;在第1次摸到红球的条件下,第2次摸到红球的概率为
;在第1次摸到红球的条件下,第2次摸到红球的概率为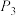 ;在第1,2次都摸到红球的条件下,第3次摸到红球的概率为
;在第1,2次都摸到红球的条件下,第3次摸到红球的概率为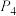 .求
.求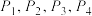 ;
;(3)对于事件
 ,当
,当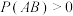 时,写出
时,写出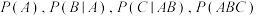 的等量关系式,并加以证明.
的等量关系式,并加以证明.
您最近一年使用:0次
2024-01-18更新
|
3688次组卷
|
9卷引用:第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第8章 概率 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)专题18 条件概率5种常见考法归类-【寒假自学课】2024年高二数学寒假提升学与练(苏教版2019)安徽省泗县第一中学2023-2024学年高二下学期第一次阶段性检测数学试卷湖南省常德市第一中学2023-2024学年高二下学期第一次月考数学试题福建省泉州市2024届高三上学期质量监测数学试题(二)(已下线)广东省深圳市深圳中学2024届高三第一次调研数学试题湖南省长沙市雅礼中学2024届高三一模数学试卷(已下线)【类题归纳】先验后验 条件概率(已下线)专题08 平面向量、概率、统计、计数原理
名校
5 . (1)对于任意两个事件 ,若
,若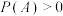 ,
,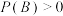 ,证明:
,证明: ;
;
(2)贝叶斯公式是由英国数学家贝叶斯发现的,它用来描述两个条件概率之间的关系.该公式为:设 ,
, ,…,
,…, 是一组两两互斥的事件,
是一组两两互斥的事件, ,且
,且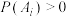 ,
, ,2,…,
,2,…, ,则对任意的事件
,则对任意的事件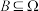 ,
,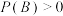 ,有
,有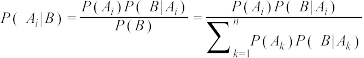 ,
, ,2,…,
,2,…, .
.
(i)已知某地区烟民的肺癌发病率为1%,先用低剂量 进行肺癌筛查,医学研究表明,化验结果是存在错误的.已知患有肺癌的人其化验结果99%呈阳性(有病),而没有患肺癌的人其化验结果99%呈阴性(无病),现某烟民的检验结果为阳性,请问他真的患肺癌的概率是多少?
进行肺癌筛查,医学研究表明,化验结果是存在错误的.已知患有肺癌的人其化验结果99%呈阳性(有病),而没有患肺癌的人其化验结果99%呈阴性(无病),现某烟民的检验结果为阳性,请问他真的患肺癌的概率是多少?
(ii)为了确保诊断无误,一般对第一次检查呈阳性的烟民进行复诊.复诊时,此人患肺癌的概率就不再是1%,这是因为第一次检查呈阳性,所以对其患肺癌的概率进行修正,因此将用贝叶斯公式求出来的概率作为修正概率,请问如果该烟民第二次检查还是呈阳性,则他真的患肺癌的概率是多少?
 ,若
,若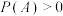 ,
,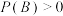 ,证明:
,证明: ;
;(2)贝叶斯公式是由英国数学家贝叶斯发现的,它用来描述两个条件概率之间的关系.该公式为:设
 ,
, ,…,
,…, 是一组两两互斥的事件,
是一组两两互斥的事件, ,且
,且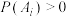 ,
, ,2,…,
,2,…, ,则对任意的事件
,则对任意的事件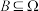 ,
,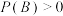 ,有
,有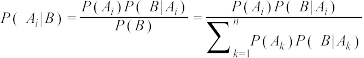 ,
, ,2,…,
,2,…, .
.(i)已知某地区烟民的肺癌发病率为1%,先用低剂量
 进行肺癌筛查,医学研究表明,化验结果是存在错误的.已知患有肺癌的人其化验结果99%呈阳性(有病),而没有患肺癌的人其化验结果99%呈阴性(无病),现某烟民的检验结果为阳性,请问他真的患肺癌的概率是多少?
进行肺癌筛查,医学研究表明,化验结果是存在错误的.已知患有肺癌的人其化验结果99%呈阳性(有病),而没有患肺癌的人其化验结果99%呈阴性(无病),现某烟民的检验结果为阳性,请问他真的患肺癌的概率是多少?(ii)为了确保诊断无误,一般对第一次检查呈阳性的烟民进行复诊.复诊时,此人患肺癌的概率就不再是1%,这是因为第一次检查呈阳性,所以对其患肺癌的概率进行修正,因此将用贝叶斯公式求出来的概率作为修正概率,请问如果该烟民第二次检查还是呈阳性,则他真的患肺癌的概率是多少?
您最近一年使用:0次
2023-04-10更新
|
2316次组卷
|
5卷引用:8.1 条件概率(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)8.1 条件概率(七大题型)-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)(已下线)第七章 随机变量及其分布(单元测试)-【同步题型讲义】2022-2023学年高二数学同步教学题型讲义(人教A版2019选择性必修第三册)湖南省长沙市第一中学2023届高三下学期月考(八)数学试题(已下线)第十章 计数原理、概率、随机变量及其分布(测试)(已下线)【类题归纳】先验后验 条件概率
名校
解题方法
6 . 2022年11月20日,卡塔尔足球世界杯正式开幕,世界杯上的中国元素随处可见.从体育场建设到电力保障,从赛场内的裁判到赛场外的吉祥物都是中国制造,为卡塔尔世界杯提供了强有力的支持.国内也再次掀起足球热潮.某地足球协会组建球队参加业余比赛,该足球队教练组为了考查球员甲对球队的贡献,作出如下数据统计(甲参加过的比赛均分出了输赢):
球队输球 | 球队赢球 | 总计 | |
甲参加 | 2 | 30 | 32 |
甲未参加 | 8 | 10 | 18 |
总计 | 10 | 40 | 50 |
(1)根据小概率值
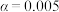 的独立性检验,能否认为该球队赢球与甲球员参赛有关联;
的独立性检验,能否认为该球队赢球与甲球员参赛有关联;(2)从该球队中任选一人,A表示事件“选中的球员参赛”,B表示事件“球队输球”.
 与
与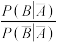 的比值是选中的球员参赛对球队贡献程度的一项度量指标,记该指标为R.
的比值是选中的球员参赛对球队贡献程度的一项度量指标,记该指标为R.①证明: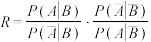 ;
;
②利用球员甲数据统计,给出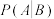 ,
,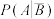 的估计值,并求出R的估计值.
的估计值,并求出R的估计值.
附: .
.
参考数据:
a | 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
您最近一年使用:0次
2023-04-06更新
|
3341次组卷
|
14卷引用:第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)湖南省长沙市望城区第一中学2022-2023学年高二下学期期末模拟数学试题(已下线)模块三 专题8 成对数据的统计分析--基础夯实练)(人教A版)(已下线)模块三 专题6 统计案例--基础夯实练(北师大2019版 高二)专题17列联表与独立性检验(已下线)专题05 成对数据的统计分析压轴题(4)吉林省吉林市普通中学2022-2023学年高三下学期第三次调研测试数学试题黑龙江省哈尔滨市第三中学校2023届高三第四次高考模拟考试数学试卷(已下线)模块八 专题10 以概率与统计为背景的压轴大题(已下线)押新高考第19题 概率统计(已下线)第02讲 成对数据的统计分析(五大题型)(讲义)(已下线)模块一 专题3 统计讲2(已下线)模块三 专题6大题分类练(统计) 拔高能力练(已下线)统 计
7 . 从有3个红球和3个蓝球的袋中,每次随机摸出1个球,摸出的球不再放回,记 表示事件“第
表示事件“第 次摸到红球”,
次摸到红球”, ,2,…,6.
,2,…,6.
(1)求第一次摸到蓝球的条件下第二次摸到红球的概率;
(2)记 表示
表示 ,
, ,
, 同时发生的概率,
同时发生的概率, 表示已知
表示已知 与
与 都发生时
都发生时 发生的概率.
发生的概率.
(ⅰ)证明: ;
;
(ⅱ)求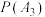 .
.
 表示事件“第
表示事件“第 次摸到红球”,
次摸到红球”, ,2,…,6.
,2,…,6.(1)求第一次摸到蓝球的条件下第二次摸到红球的概率;
(2)记
 表示
表示 ,
, ,
, 同时发生的概率,
同时发生的概率, 表示已知
表示已知 与
与 都发生时
都发生时 发生的概率.
发生的概率.(ⅰ)证明:
 ;
;(ⅱ)求
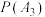 .
.
您最近一年使用:0次
2023-01-12更新
|
946次组卷
|
5卷引用:8.1 条件概率(含8.1.1-8.1.3)(练习)-2022-2023学年高二数学同步精品课堂(苏教版2019选择性必修第二册)
(已下线)8.1 条件概率(含8.1.1-8.1.3)(练习)-2022-2023学年高二数学同步精品课堂(苏教版2019选择性必修第二册)(已下线)第七章 随机变量及其分布(A卷·知识通关练)(1)湖北省部分重点中学2023届高三上学期1月第二次联考数学试题(已下线)大题强化训练(5)湖北省恩施州高中教育联盟2023届高三上学期期末数学试题