名校
1 . 刷脸时代来了,人们为“刷脸支付”给生活带来的便捷感到高兴,但“刷脸支付”的安全性也引起了人们的担忧.某调查机构为了解人们对“刷脸支付”的接受程度,通过安全感问卷进行调查(问卷得分在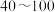 分之间),并从参与者中随机抽取
分之间),并从参与者中随机抽取 人.根据调查结果绘制出如图所示的频率分布直方图.
人.根据调查结果绘制出如图所示的频率分布直方图.
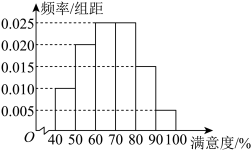
(1)据此估计这 人满意度的平均数
人满意度的平均数 同一组中的数据用该组区间的中点值作代表
同一组中的数据用该组区间的中点值作代表 ;
;
(2)某大型超市引入“刷脸支付”后,在推广“刷脸支付”期间,推出两种付款方案:方案一:不采用“刷脸支付”,无任何优惠,但可参加超市的抽奖返现金活动.活动方案为:从装有 个形状、大小完全相同的小球
个形状、大小完全相同的小球 其中红球
其中红球 个,黑球
个,黑球 个
个 的抽奖盒中,一次性摸出
的抽奖盒中,一次性摸出 个球,若摸到
个球,若摸到 个红球,返消费金额的
个红球,返消费金额的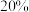 ;若摸到
;若摸到 个红球,返消费金额的
个红球,返消费金额的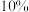 ,除此之外不返现金.
,除此之外不返现金.
方案二:采用“刷脸支付”,此时对购物的顾客随机优惠,但不参加超市的抽奖返现金活动,根据统计结果得知,使用“刷脸支付”时有 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受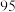 折优惠.现小张在该超市购买了总价为
折优惠.现小张在该超市购买了总价为 元的商品.
元的商品.
①求小张选择方案一付款时实际付款额 的分布列与数学期望;
的分布列与数学期望;
②试从期望角度,比较小张选择方案一与方案二付款,哪个方案更划算?(注:结果精确到 )
)
 分之间),并从参与者中随机抽取
分之间),并从参与者中随机抽取 人.根据调查结果绘制出如图所示的频率分布直方图.
人.根据调查结果绘制出如图所示的频率分布直方图.
(1)据此估计这
 人满意度的平均数
人满意度的平均数 同一组中的数据用该组区间的中点值作代表
同一组中的数据用该组区间的中点值作代表 ;
;(2)某大型超市引入“刷脸支付”后,在推广“刷脸支付”期间,推出两种付款方案:方案一:不采用“刷脸支付”,无任何优惠,但可参加超市的抽奖返现金活动.活动方案为:从装有
 个形状、大小完全相同的小球
个形状、大小完全相同的小球 其中红球
其中红球 个,黑球
个,黑球 个
个 的抽奖盒中,一次性摸出
的抽奖盒中,一次性摸出 个球,若摸到
个球,若摸到 个红球,返消费金额的
个红球,返消费金额的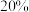 ;若摸到
;若摸到 个红球,返消费金额的
个红球,返消费金额的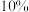 ,除此之外不返现金.
,除此之外不返现金.方案二:采用“刷脸支付”,此时对购物的顾客随机优惠,但不参加超市的抽奖返现金活动,根据统计结果得知,使用“刷脸支付”时有
 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受 折优惠,有
折优惠,有 的概率享受
的概率享受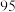 折优惠.现小张在该超市购买了总价为
折优惠.现小张在该超市购买了总价为 元的商品.
元的商品.①求小张选择方案一付款时实际付款额
 的分布列与数学期望;
的分布列与数学期望;②试从期望角度,比较小张选择方案一与方案二付款,哪个方案更划算?(注:结果精确到
 )
)
您最近一年使用:0次
2024-04-30更新
|
1878次组卷
|
7卷引用:专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)
(已下线)专题05 离散型随机变量的分布列常考点(8类题型)-备战2023-2024学年高二数学下学期期末真题分类汇编(江苏专用)宁夏回族自治区石嘴山市平罗中学2024届高三下学期第三次模拟考试数学(理)试题(已下线)9.1 随机抽样与统计图标(高考真题素材之十年高考)上海市金山中学2023-2024学年高二下学期5月月考数学试卷湖南省长沙市长郡中学2024届高三下学期模拟(三)数学试题辽宁省沈阳市东北育才学校2024届高三考前最后一模数学试题广东省茂名市高州中学2025届高三上学期8月月考数学试题
名校
2 . 某学校号召学生参加“每天锻炼1小时”活动,为了解学生参加活动的情况,统计了全校所有学生在假期每周锻炼的时间,现随机抽取了60名同学在某一周参加锻炼的数据,整理如下 列联表:
列联表:
注:将一周参加锻炼时间不小于3小时的称为“经常锻炼”,其余的称为“不经常锻炼”.
(1)请完成上面 列联表,并依据小概率值
列联表,并依据小概率值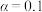 的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;
的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;
(2)将一周参加锻炼为0小时的称为“极度缺乏锻炼”.在抽取的60名同学中有5人“极度缺乏锻炼”.以样本频率估计概率.若在全校抽取20名同学,设“极度缺乏锻炼”的人数为X,求X的数学期望 和方差
和方差 ;
;
(3)将一周参加锻炼6小时以上的同学称为“运动爱好者”.在抽取的60名同学中有10名“运动爱好者”,其中有7名男生,3名女生.为进一步了解他们的生活习惯,在10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为Y,求Y的分布列和数学期望.
附: ,
,
 列联表:
列联表:性别 | 不经常锻炼 | 经常锻炼 | 合计 |
男生 | 7 | ||
女生 | 16 | 30 | |
合计 | 21 |
(1)请完成上面
 列联表,并依据小概率值
列联表,并依据小概率值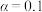 的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;
的独立性检验,能否认为性别因素与学生锻炼的经常性有关系;(2)将一周参加锻炼为0小时的称为“极度缺乏锻炼”.在抽取的60名同学中有5人“极度缺乏锻炼”.以样本频率估计概率.若在全校抽取20名同学,设“极度缺乏锻炼”的人数为X,求X的数学期望
 和方差
和方差 ;
;(3)将一周参加锻炼6小时以上的同学称为“运动爱好者”.在抽取的60名同学中有10名“运动爱好者”,其中有7名男生,3名女生.为进一步了解他们的生活习惯,在10名“运动爱好者”中,随机抽取3人进行访谈,设抽取的3人中男生人数为Y,求Y的分布列和数学期望.
附:
 ,
,
| 0.1 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |
您最近一年使用:0次
2024-05-09更新
|
1767次组卷
|
12卷引用:江苏省盐城中学、南京二十九中联考2023-2024学年高二下学期4月期中数学试题
江苏省盐城中学、南京二十九中联考2023-2024学年高二下学期4月期中数学试题江苏省苏州实验中学2023-2024学年高二下学期5月月考数学试题江苏省淮安市洪泽中学,金湖中学,清河中学,清浦中学等学校2023-2024学年高二下学期5月月考数学试题(已下线)专题07 回归方程与独立性检验--高二期末考点大串讲(苏教版2019选择性必修第二册)湖北省部分重点中学2023-2024学年高二下学期五月联考数学试卷广东省江门市鹤山市第一中学2023-2024学年高二下学期第二阶段考试(5月)数学试题山东省滕州市第五中学2023-2024学年高二下学期第四次单元检测(第二次月考)数学试题福建省福州市闽侯县第一中学2023-2024学年高二下学期第二次月考(5月)数学试题辽宁省七校协作体2023-2024学年高二下学期6月月考数学试题江西省南昌市第十中学2023-2024学年高二下学期第二次月考数学试题黑龙江省哈尔滨市双城区兆麟中学2023-2024学年高二下学期第二次月考(6月)数学试题(已下线)第1套 期末全真模拟卷(高二期末中等卷)
名校
3 . 某工厂引进新的生产设备 ,为对其进行评估,从设备
,为对其进行评估,从设备 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
经计算,样本的平均值 ,标准差
,标准差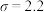 ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.
(1)为评估设备 对原材料的利用情况,需要研究零件中某材料含量
对原材料的利用情况,需要研究零件中某材料含量 和原料中的该材料含量
和原料中的该材料含量 之间的相关关系,现取了8对观测值,求
之间的相关关系,现取了8对观测值,求 与
与 的线性回归方程.
的线性回归方程.
(2)为评判设备 生产零件的性能,从该设备加工的零件中任意抽取一件,记其直径为
生产零件的性能,从该设备加工的零件中任意抽取一件,记其直径为 ,并根据以下不等式进行评判(
,并根据以下不等式进行评判( 表示相应事件的概率);
表示相应事件的概率);
①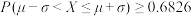 ;②
;②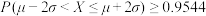 ;③
;③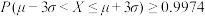 .
.
评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备 的性能等级.
的性能等级.
(3)将直径小于等于 或直径大于
或直径大于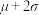 的零件认为是次品.从样本中随意抽取2件零件,再从设备
的零件认为是次品.从样本中随意抽取2件零件,再从设备 的生产流水线上随意抽取2件零件,计算其中次品总数
的生产流水线上随意抽取2件零件,计算其中次品总数 的数学期望
的数学期望 .
.
附:①对于一组数据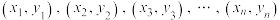 ,其回归直线
,其回归直线 的斜率和截距的最小二乘法估计公式分别为
的斜率和截距的最小二乘法估计公式分别为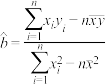 ,
,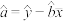 ;
;
②参考数据: ,
, ,
, ,
,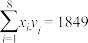 .
.
 ,为对其进行评估,从设备
,为对其进行评估,从设备 生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:| 直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
| 件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
 ,标准差
,标准差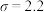 ,以频率值作为概率的估计值.
,以频率值作为概率的估计值.(1)为评估设备
 对原材料的利用情况,需要研究零件中某材料含量
对原材料的利用情况,需要研究零件中某材料含量 和原料中的该材料含量
和原料中的该材料含量 之间的相关关系,现取了8对观测值,求
之间的相关关系,现取了8对观测值,求 与
与 的线性回归方程.
的线性回归方程.(2)为评判设备
 生产零件的性能,从该设备加工的零件中任意抽取一件,记其直径为
生产零件的性能,从该设备加工的零件中任意抽取一件,记其直径为 ,并根据以下不等式进行评判(
,并根据以下不等式进行评判( 表示相应事件的概率);
表示相应事件的概率);①
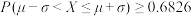 ;②
;②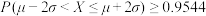 ;③
;③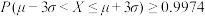 .
.评判规则为:若同时满足上述三个不等式,则设备等级为甲;仅满足其中两个,则等级为乙;若仅满足其中一个,则等级为丙;若全部不满足,则等级为丁,试判断设备
 的性能等级.
的性能等级.(3)将直径小于等于
 或直径大于
或直径大于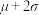 的零件认为是次品.从样本中随意抽取2件零件,再从设备
的零件认为是次品.从样本中随意抽取2件零件,再从设备 的生产流水线上随意抽取2件零件,计算其中次品总数
的生产流水线上随意抽取2件零件,计算其中次品总数 的数学期望
的数学期望 .
.附:①对于一组数据
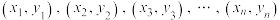 ,其回归直线
,其回归直线 的斜率和截距的最小二乘法估计公式分别为
的斜率和截距的最小二乘法估计公式分别为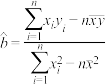 ,
,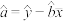 ;
;②参考数据:
 ,
, ,
, ,
,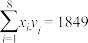 .
.
您最近一年使用:0次
2023-12-22更新
|
1681次组卷
|
8卷引用:第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)
(已下线)第9章 统计 章末题型归纳总结-【帮课堂】2023-2024学年高二数学同步学与练(苏教版2019选择性必修第二册)福建省漳州市东山第二中学2022-2023学年高二下学期期中数学试题江西省赣州市南康中学2024届高三上学期七省联考考前数学猜题卷(六)重庆缙云教育联盟2024届高三高考第一次诊断性检测数学试卷陕西省西安市西安南开高级中学2023-2024学年高二上学期期末考试数学试题(已下线)专题05 成对数据的统计分析压轴题(2)(已下线)第八章 成对数据的统计分析(压轴题专练)-2023-2024学年高二数学单元速记·巧练(人教A版2019选择性必修第三册)(已下线)专题3 变量的相关性、回归分析压轴大题(过关集训)





