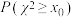名校
1 . 下列命题中真命题是( )
A.设一组数据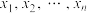 的平均数为 的平均数为 ,方差为 ,方差为 ,则 ,则 |
B.已知随机变量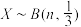 ,若 ,若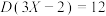 ,则 ,则 |
C.两个变量的相关系数 越大,它们的相关程度越强 越大,它们的相关程度越强 |
D.若随机变量 服从正态分布 服从正态分布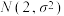 ,且 ,且 ,则 ,则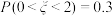 |
您最近半年使用:0次
名校
解题方法
2 . 已知随机变量 ,随机变量
,随机变量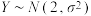 ,若
,若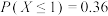 ,
,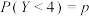 ,则
,则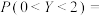 ( )
( )
 ,随机变量
,随机变量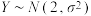 ,若
,若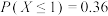 ,
,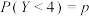 ,则
,则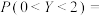 ( )
( )| A.0.1 | B.0.2 | C.0.3 | D.0.4 |
您最近半年使用:0次
2023-06-14更新
|
608次组卷
|
5卷引用:江西省宜春市丰城市第九中学(日新班)2022-2023学年高一下学期期末考试数学试题
江西省宜春市丰城市第九中学(日新班)2022-2023学年高一下学期期末考试数学试题江苏省淮阴中学等三校2022-2023学年高二下学期联考数学试题重庆市西北狼教育联盟2024届高三上学期开学考试数学试题(已下线)第08讲 两点分布、二项分布、超几何分布与正态分布(十一大题型)(讲义)-2河北省部分学校2023-2024学年高三上学期六调考试数学试题
名校
解题方法
3 . 下列说法正确的是( )
A.设随机变量 服从二项分布 服从二项分布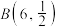 ,则 ,则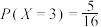 |
B.已知随机变量 服从正态分布 服从正态分布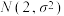 ,且 ,且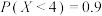 ,则 ,则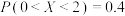 |
C.甲、乙、丙三人均准备在3个旅游景点中任选一处去游玩,则在至少有1个景点未被选择的条件下,恰有2个景点未被选择的概率是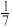 |
D. , , |
您最近半年使用:0次
2022-04-18更新
|
1560次组卷
|
8卷引用:江西省景德镇一中2021-2022学年高一(18班)下学期期末考数学试题
江西省景德镇一中2021-2022学年高一(18班)下学期期末考数学试题人教A版(2019) 选修第三册 过关斩将 第七章 本章达标检测浙江省金华市东阳市横店高级中学2021-2022学年高二下学期4月月考数学试题河北省深州市长江中学2021-2022学年高二下学期5月月考数学试题山东省菏泽市曹县第一中学2021-2022学年高二下学期第二次月考数学试题河北省石家庄十五中2021-2022学年高二下学期6月第三次考数学试题(已下线)第7章 随机变量及其分布(单元测试)-【上好课】2022-2023学年高二数学同步备课系列(人教A版2019选择性必修第三册)湖南省岳阳市平江县颐华高级中学2023-2024学年高三上学期入学考试数学试题
名校
4 . 已知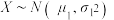 ,
,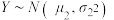 ,
,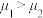 ,
, ,
, ,则下列结论中一定成立的有( )
,则下列结论中一定成立的有( )
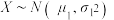 ,
,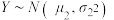 ,
,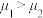 ,
, ,
, ,则下列结论中一定成立的有( )
,则下列结论中一定成立的有( )A.若 ,则 ,则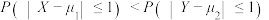 |
B.若 ,则 ,则 |
C.若 ,则 ,则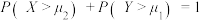 |
D.若 ,则 ,则 |
您最近半年使用:0次
2021-05-16更新
|
1930次组卷
|
10卷引用:江苏省扬州中学2020-2021学年高一(早培)下学期5月月考考数学试题
2021高三·全国·专题练习
名校
5 . 某市教育科学研究院为了对今后所出试题的难度有更好的把握,提高命题质量,对该市高三联考理综试卷的得分情况进行了调研.从全市参加考试的考生中随机抽取了100名考生的理综成绩,将数据分成7组:[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300].并整理得到如图所示的频率分布直方图.
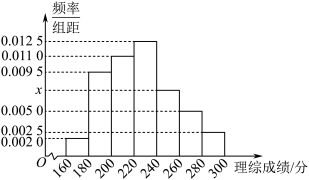
(1)根据频率分布直方图,求直方图中x的值;
(2)用频率估计概率,从该市所有高三考生的理综成绩中随机抽取3个,记理综成绩位于区间[220,260)内的个数为y,求y的分布列及数学期望E(y);
(3)若变量S满足P(μ﹣σ<S≤μ+σ)≈0.6827,且P(μ﹣2σ<S≤μ+2 σ)≈0.9545,则称S近似服从正态分布N(μ,σ2),若该市高三考生的理综成绩近似服从正态分布N(225,225),则给予这套试卷好评,否则差评,试问:这套试卷得到好评还是差评?

(1)根据频率分布直方图,求直方图中x的值;
(2)用频率估计概率,从该市所有高三考生的理综成绩中随机抽取3个,记理综成绩位于区间[220,260)内的个数为y,求y的分布列及数学期望E(y);
(3)若变量S满足P(μ﹣σ<S≤μ+σ)≈0.6827,且P(μ﹣2σ<S≤μ+2 σ)≈0.9545,则称S近似服从正态分布N(μ,σ2),若该市高三考生的理综成绩近似服从正态分布N(225,225),则给予这套试卷好评,否则差评,试问:这套试卷得到好评还是差评?
您最近半年使用:0次
2021-03-16更新
|
1635次组卷
|
7卷引用:第14章 统计(能力提升)-2020-2021学年高一数学单元测试定心卷(苏教版2019必修第二册)
(已下线)第14章 统计(能力提升)-2020-2021学年高一数学单元测试定心卷(苏教版2019必修第二册)第六章 统计 单元综合测试卷-2021-2022学年高一上学期数学北师大版(2019)必修第一册(已下线)大题专练训练49:随机变量的分布列(正态分布)-2021届高三数学二轮复习广东省湛江市第二十一中学2020-2021学年高二下学期期中数学试题(已下线)7.5正态分布-【上好课】2020-2021学年高二数学同步备课系列(人教A版2019选择性必修第三册)(已下线)第二章 概率(基础过关)-2020-2021学年高二数学单元测试定心卷(北师大版选修2-3)湖南省常德市第二中学2020-2021学年高二(332班)下学期期中数学试题
名校
解题方法
6 . 2020年初,新型冠状病毒(2019-nCoV)肆虐,全民开启防疫防控.新型冠状病毒的传染主要是人与人之间进行传播,感染人群年龄大多数是40岁以上人群.该病毒进入人体后有潜伏期,潜伏期是指病原体侵入人体至最早出现临床症状的这段时间.潜伏期越长,感染到他人的可能性越高,现对200个病例的潜伏期(单位:天)进行调查,统计发现潜伏期平均数为7.1,方差为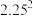 .如果认为超过8天的潜伏期属于“长潜伏期”,按照年龄统计样本,得到下面的列联表:
.如果认为超过8天的潜伏期属于“长潜伏期”,按照年龄统计样本,得到下面的列联表:
(1)是否有95%的把握认为“长期潜伏”与年龄有关;
(2)假设潜伏期X服从正态分布 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .
.
(ⅰ)现在很多省份对入境旅客一律要求隔离14天,请用概率的知识解释其合理性;
(ⅱ)以题目中的样本频率估计概率,设1000个病例中恰有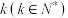 个属于“长期潜伏”的概率是
个属于“长期潜伏”的概率是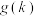 ,当k为何值时,
,当k为何值时,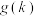 取得最大值.
取得最大值.
附:
若 则
则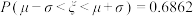 .
. ,
,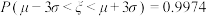 .
.
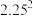 .如果认为超过8天的潜伏期属于“长潜伏期”,按照年龄统计样本,得到下面的列联表:
.如果认为超过8天的潜伏期属于“长潜伏期”,按照年龄统计样本,得到下面的列联表:年龄/人数 | 长期潜伏 | 非长期潜伏 |
40岁以上 | 30 | 110 |
40岁及40岁以下 | 20 | 40 |
(1)是否有95%的把握认为“长期潜伏”与年龄有关;
(2)假设潜伏期X服从正态分布
 ,其中
,其中 近似为样本平均数
近似为样本平均数 ,
, 近似为样本方差
近似为样本方差 .
.(ⅰ)现在很多省份对入境旅客一律要求隔离14天,请用概率的知识解释其合理性;
(ⅱ)以题目中的样本频率估计概率,设1000个病例中恰有
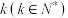 个属于“长期潜伏”的概率是
个属于“长期潜伏”的概率是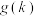 ,当k为何值时,
,当k为何值时,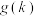 取得最大值.
取得最大值.附:

| 0.1 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
若
 则
则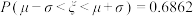 .
. ,
,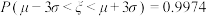 .
.
您最近半年使用:0次
2020-08-10更新
|
515次组卷
|
3卷引用:江苏省扬州中学2020-2021学年高一(早培)下学期5月月考考数学试题
解题方法
7 . 已知某种零件的尺寸ξ(单位:mm)服从正态分布,其正态曲线在(0,80)上是增函数,在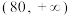 上是减函数,且
上是减函数,且 .
.
(1)求概率密度函数;
(2)估计尺寸在72mm~88mm间的零件大约占总数的百分之几?
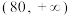 上是减函数,且
上是减函数,且 .
.(1)求概率密度函数;
(2)估计尺寸在72mm~88mm间的零件大约占总数的百分之几?
您最近半年使用:0次
2017-11-27更新
|
611次组卷
|
7卷引用:高中数学人教版 选修2-3(理科) 第二章 随机变量及其分布 2.4正态分布
高中数学人教版 选修2-3(理科) 第二章 随机变量及其分布 2.4正态分布(已下线)2013-2014学年苏教版选修2-3高二数学双基达标2.6练习卷(已下线)同步君人教A版选修2-3第二章2.4正态分布2018-2019学年北师大版高中数学选修2-3同步配套(课件+练习):2.6(已下线)3.3 正态分布人教B版(2019) 选修第二册 北京名校同步练习册 第四章 概率与统计 4.2随机变量 4.2.5正态分布湘教版(2019)选择性必修第二册课本习题 习题3.3
解题方法
8 . 某县农民年均收入服从μ=500元,σ=20元的正态分布,求:
(1)此县农民的年均收入在500~520元之间的人数的百分比;
(2)此县农民的年均收入超过540元的人数的百分比.
(1)此县农民的年均收入在500~520元之间的人数的百分比;
(2)此县农民的年均收入超过540元的人数的百分比.
您最近半年使用:0次
解题方法
9 . 已知一次考试共有60名同学参加,考生的成绩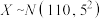 ,据此估计,大约应有57人的分数在下列哪个区间内( )
,据此估计,大约应有57人的分数在下列哪个区间内( )
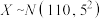 ,据此估计,大约应有57人的分数在下列哪个区间内( )
,据此估计,大约应有57人的分数在下列哪个区间内( )| A.(90,110] | B.(95,125] |
| C.(100,120] | D.(105,115] |
您最近半年使用:0次
2017-11-27更新
|
873次组卷
|
3卷引用:高中数学人教版 选修2-3(理科) 第二章 随机变量及其分布 2.4正态分布
高中数学人教版 选修2-3(理科) 第二章 随机变量及其分布 2.4正态分布(已下线)同步君人教A版选修2-3第二章2.4正态分布黑龙江省海林市朝鲜族中学人教版高中数学选修2-3同步练习:2.4 正态分布
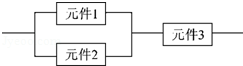
10 . 某一部件由三个电子元件按如图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为

A. | B.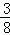 | C. | D. |
您最近半年使用:0次