名校
1 . 我们可以把平面向量坐标的概念推广为“复向量”,即可将有序复数对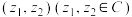 视为一个向量,记作
视为一个向量,记作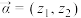 .类比平面向量的线性运算可以定义复向量的线性运算;两个复向量
.类比平面向量的线性运算可以定义复向量的线性运算;两个复向量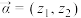 ,
, 的数量积记作
的数量积记作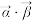 ,定义为
,定义为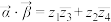 ;复向量
;复向量 的模定义为
的模定义为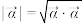 .
.
(1)设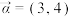 ,
,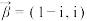 ,求复向量
,求复向量 与
与 的模;
的模;
(2)已知对任意的实向量 与
与 ,都有
,都有 ,当且仅当
,当且仅当 与
与 平行时取等号;
平行时取等号;
①求证:对任意实数a,b,c,d,不等式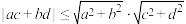 成立,并写出此不等式的取等条件;
成立,并写出此不等式的取等条件;
②求证:对任意两个复向量 与
与 ,不等式
,不等式 仍然成立;
仍然成立;
(3)当 时,称复向量
时,称复向量 与
与 平行.设
平行.设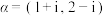 ,
,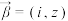 ,
,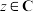 ,若复向量
,若复向量 与
与 平行,求复数z的值.
平行,求复数z的值.
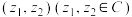 视为一个向量,记作
视为一个向量,记作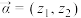 .类比平面向量的线性运算可以定义复向量的线性运算;两个复向量
.类比平面向量的线性运算可以定义复向量的线性运算;两个复向量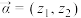 ,
, 的数量积记作
的数量积记作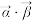 ,定义为
,定义为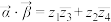 ;复向量
;复向量 的模定义为
的模定义为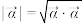 .
.(1)设
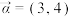 ,
,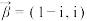 ,求复向量
,求复向量 与
与 的模;
的模;(2)已知对任意的实向量
 与
与 ,都有
,都有 ,当且仅当
,当且仅当 与
与 平行时取等号;
平行时取等号;①求证:对任意实数a,b,c,d,不等式
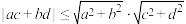 成立,并写出此不等式的取等条件;
成立,并写出此不等式的取等条件;②求证:对任意两个复向量
 与
与 ,不等式
,不等式 仍然成立;
仍然成立;(3)当
 时,称复向量
时,称复向量 与
与 平行.设
平行.设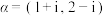 ,
,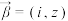 ,
,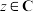 ,若复向量
,若复向量 与
与 平行,求复数z的值.
平行,求复数z的值.
您最近一年使用:0次
2024-05-23更新
|
519次组卷
|
4卷引用:专题6 以新定义为背景的相关问题【练】(高一期末压轴专项)
(已下线)专题6 以新定义为背景的相关问题【练】(高一期末压轴专项)黑龙江省哈尔滨市第九中学校2023-2024学年高一下学期期中学业阶段评价考试数学试卷重庆市万州第二高级中学2024-2025学年高二上学期入学考试数学检测试卷山东省济宁市北大新世纪邹城实验学校2023-2024学年高一下学期期末考试数学试题
名校
2 . 在复数城内,大小成为了没有意义的量,那么我们能否赋予它一个定义呢,在实数域内,我们通常用绝对值来描述大小,而复数域中也相应的有复数的模长来代替绝对值,于是,我们只需定义复数的正负即可,我们规定复数的“长度”即为模长,规定在复平面x轴上方的复数为正,在x轴下方的复数为负,在x轴上的复数即为实数大小.“大小”用符号+“长度”表示,我们用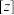 来表示复数的“大小”,例如:
来表示复数的“大小”,例如: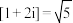 ,
, ,
, ,
, ,
,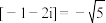 ,则下列说法正确的是( )
,则下列说法正确的是( )
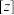 来表示复数的“大小”,例如:
来表示复数的“大小”,例如: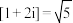 ,
, ,
, ,
, ,
,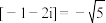 ,则下列说法正确的是( )
,则下列说法正确的是( )A. 在复平面内表示一个圆 在复平面内表示一个圆 |
B.若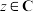 ,则方程 ,则方程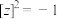 无解 无解 |
C.若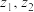 为虚数,且 为虚数,且 ,则 ,则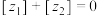 |
D.复平面内,复数 对应的点在直线 对应的点在直线 上,则 上,则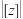 最小值为 最小值为 |
您最近一年使用:0次
名校
解题方法
3 . 在复数域内,大小成为了没有意义的量,那么我们能否赋予它一个定义呢,在实数域内,我们通常用绝对值来描述大小,而复数域中也相应的有复数的模长来代替绝对值,于是,我们只需定义复数的正负即可,我们规定复数的“长度”即为模长,规定在复平面 轴上方的复数为正,在
轴上方的复数为正,在 轴下方的复数为负,在
轴下方的复数为负,在 轴上的复数即为实数大小.“大小”用符号+“长度”表示,我们用
轴上的复数即为实数大小.“大小”用符号+“长度”表示,我们用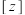 来表示复数的“大小”,例如:
来表示复数的“大小”,例如: ,则下列说法正确的是( )
,则下列说法正确的是( )
 轴上方的复数为正,在
轴上方的复数为正,在 轴下方的复数为负,在
轴下方的复数为负,在 轴上的复数即为实数大小.“大小”用符号+“长度”表示,我们用
轴上的复数即为实数大小.“大小”用符号+“长度”表示,我们用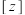 来表示复数的“大小”,例如:
来表示复数的“大小”,例如: ,则下列说法正确的是( )
,则下列说法正确的是( )A.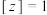 在复平面内表示一个圆 在复平面内表示一个圆 |
B.若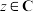 ,则方程 ,则方程 无解 无解 |
C.若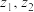 为虚数,且 为虚数,且 ,则 ,则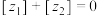 |
D.复数 满足 满足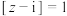 ,则 ,则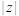 的取值范围为 的取值范围为 |
您最近一年使用:0次



